Description: Definition of the
conditional operator for propositions. The value of
if-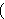    
 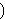 is is  if if  is true and is true and  if if  false. See dfifp2 1014, dfifp3 1015, dfifp4 1016, dfifp5 1017, dfifp6 1018 and
dfifp7 1019 for alternate definitions.
false. See dfifp2 1014, dfifp3 1015, dfifp4 1016, dfifp5 1017, dfifp6 1018 and
dfifp7 1019 for alternate definitions.
This definition (in the form of dfifp2 1014) appears in Section II.24 of
[Church] p. 129 (Definition D12 page 132),
where it is called "conditioned
disjunction". Church's 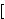      ![] ]](rbrack.gif) corresponds to our
if-
corresponds to our
if-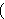    
 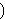 (note the permutation of the first two
variables). (note the permutation of the first two
variables).
Church uses the conditional operator as an intermediate step to prove
completeness of some systems of connectives. The first result is that the
system 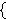 if- if- 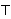  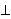 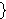 is
complete: for the induction step, consider
a wff with n+1 variables; single out one variable, say is
complete: for the induction step, consider
a wff with n+1 variables; single out one variable, say  ; when one
sets ; when one
sets  to
True (resp. False), then what remains is a wff of n
variables, so by the induction hypothesis it corresponds to a formula
using only to
True (resp. False), then what remains is a wff of n
variables, so by the induction hypothesis it corresponds to a formula
using only 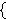 if- if- 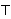  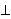 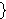 , say , say  (resp.
(resp.  );
therefore,
the formula if- );
therefore,
the formula if-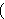    
 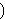 represents the initial wff. Now,
since represents the initial wff. Now,
since 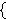 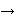  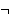 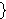 and similar systems suffice to express
if- and similar systems suffice to express
if- 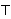  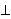 , they are also complete. , they are also complete.
(Contributed by BJ, 22-Jun-2019.) |