 |
Eigen
3.2.7
|
 |
Eigen
3.2.7
|
Class to view a vector of integers as a permutation matrix.
| _IndicesType | the type of the vector of integer (can be any compatible expression) |
This class allows to view any vector expression of integers as a permutation matrix.
 Inheritance diagram for PermutationWrapper< _IndicesType >:
Inheritance diagram for PermutationWrapper< _IndicesType >:Public Member Functions | |
| PermutationWrapper < _IndicesType > & | applyTranspositionOnTheLeft (Index i, Index j) |
| PermutationWrapper < _IndicesType > & | applyTranspositionOnTheRight (Index i, Index j) |
| Index | cols () const |
| Derived & | derived () |
| const Derived & | derived () const |
| Index | determinant () const |
| IndicesType & | indices () |
| const internal::remove_all < typename IndicesType::Nested > ::type & | indices () const |
| Transpose< PermutationBase > | inverse () const |
| PlainPermutationType | operator* (const PermutationBase< Other > &other) const |
| PlainPermutationType | operator* (const Transpose< PermutationBase< Other > > &other) const |
| void | resize (Index newSize) |
| Index | rows () const |
| void | setIdentity () |
| void | setIdentity (Index newSize) |
| Index | size () const |
| DenseMatrixType | toDenseMatrix () const |
| Transpose< PermutationBase > | transpose () const |
|
inlineinherited |
Multiplies *this by the transposition 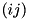 on the left.
on the left.
|
inlineinherited |
Multiplies *this by the transposition 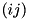 on the right.
on the right.
This is a fast operation, it only consists in swapping two indices.
|
inlineinherited |
|
inlineinherited |
Referenced by IterativeSolverBase< ConjugateGradient< _MatrixType, _UpLo, _Preconditioner > >::analyzePattern(), MatrixBase< Derived >::applyOnTheLeft(), MatrixBase< Derived >::applyOnTheRight(), PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::applyTranspositionOnTheLeft(), PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::applyTranspositionOnTheRight(), SparseMatrixBase< CwiseBinaryOp< BinaryOp, Lhs, Rhs > >::bottomRows(), EigenBase< SparseSymmetricPermutationProduct< MatrixType, UpLo > >::cols(), SparseMatrixBase< CwiseBinaryOp< BinaryOp, Lhs, Rhs > >::cols(), IterativeSolverBase< ConjugateGradient< _MatrixType, _UpLo, _Preconditioner > >::compute(), SparseMatrixBase< CwiseBinaryOp< BinaryOp, Lhs, Rhs > >::eval(), IterativeSolverBase< ConjugateGradient< _MatrixType, _UpLo, _Preconditioner > >::factorize(), PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::indices(), PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::inverse(), IterativeSolverBase< ConjugateGradient< _MatrixType, _UpLo, _Preconditioner > >::IterativeSolverBase(), RotationBase< Derived, 3 >::operator*(), SparseSelfAdjointView< MatrixType, UpLo >::operator*(), PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::operator*(), SparseMatrixBase< Derived >::operator*(), SparseMatrixBase< CwiseBinaryOp< BinaryOp, Lhs, Rhs > >::operator*(), Transform< Scalar, Dim, Mode, _Options >::operator*(), Eigen::operator*(), MatrixBase< Derived >::operator*=(), PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::operator=(), DenseBase< Derived >::operator=(), Transform< Scalar, Dim, Mode, _Options >::operator=(), PlainObjectBase< Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::operator=(), PlainObjectBase< Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::PlainObjectBase(), SparseMatrixBase< CwiseBinaryOp< BinaryOp, Lhs, Rhs > >::real(), PlainObjectBase< Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::resizeLike(), EigenBase< SparseSymmetricPermutationProduct< MatrixType, UpLo > >::rows(), SparseMatrixBase< CwiseBinaryOp< BinaryOp, Lhs, Rhs > >::rows(), SimplicialCholeskyBase< SimplicialLDLT< _MatrixType, _UpLo, _Ordering > >::solve(), IterativeSolverBase< ConjugateGradient< _MatrixType, _UpLo, _Preconditioner > >::solve(), SparseLU< _MatrixType, _OrderingType >::solve(), UmfPackLU< _MatrixType >::solve(), CholmodBase< _MatrixType, _UpLo, CholmodSimplicialLLT< _MatrixType, _UpLo > >::solve(), SuperLUBase< _MatrixType, SuperILU< _MatrixType > >::solve(), SparseMatrix< Scalar, RowMajor >::SparseMatrix(), PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::toDenseMatrix(), SparseMatrixBase< CwiseBinaryOp< BinaryOp, Lhs, Rhs > >::topLeftCorner(), Transform< Scalar, Dim, Mode, _Options >::Transform(), PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::transpose(), and SparseMatrixBase< CwiseBinaryOp< BinaryOp, Lhs, Rhs > >::twistedBy().
|
inlineinherited |
|
inlineinherited |
This function is O(n) procedure allocating a buffer of n booleans.
|
inlineinherited |
|
inline |
const version of indices().
|
inlineinherited |
|
inlineinherited |
|
inlineinherited |
|
inlineinherited |
Resizes to given size.
|
inlineinherited |
|
inlineinherited |
Sets *this to be the identity permutation matrix
|
inlineinherited |
Sets *this to be the identity permutation matrix of given size.
|
inlineinherited |
|
inlineinherited |
|
inlineinherited |