Detailed Description

template<typename Scalar, int Options = AutoAlign>
class Eigen::Quaternion< Scalar, Options >

The quaternion class used to represent 3D orientations and rotations.

This is defined in the Geometry module.

#include <Eigen/Geometry>

Template Parameters

_Scalar	the scalar type, i.e., the type of the coefficients
_Options	controls the memory alignment of the coefficients. Can be # AutoAlign or # DontAlign. Default is AutoAlign.

This class represents a quaternion 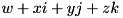$ w+xi+yj+zk $ that is a convenient representation of orientations and rotations of objects in three dimensions. Compared to other representations like Euler angles or 3x3 matrices, quaternions offer the following advantages:

compact storage (4 scalars)
efficient to compose (28 flops),
stable spherical interpolation

The following two typedefs are provided for convenience:

Quaternionf for float
Quaterniond for double

Warning: Operations interpreting the quaternion as rotation have undefined behavior if the quaternion is not normalized.

See Also: class AngleAxis, class Transform

Inheritance diagram for Quaternion< Scalar, Options >:

Public Types
typedef Matrix< Scalar, 3, 3 >	Matrix3

typedef Matrix< Scalar, Dim, Dim >	RotationMatrixType

typedef Matrix< Scalar, 3, 1 >	Vector3

Public Member Functions
Vector3	_transformVector (const Vector3 &v) const

internal::cast_return_type < Quaternion< _Scalar, _Options >, Quaternion < NewScalarType > >::type	cast () const

Quaternion< Scalar >	conjugate () const

Scalar	dot (const QuaternionBase< OtherDerived > &other) const

template<typename Derived1 , typename Derived2 >
Quaternion< Scalar, Options >	FromTwoVectors (const MatrixBase< Derived1 > &a, const MatrixBase< Derived2 > &b)

Quaternion< Scalar >	inverse () const

bool	isApprox (const QuaternionBase< OtherDerived > &other, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const

RotationMatrixType	matrix () const

Scalar	norm () const

void	normalize ()

Quaternion< Scalar >	normalized () const

Transform< Scalar, Dim, Isometry >	operator* (const Translation< Scalar, Dim > &t) const

RotationMatrixType	operator* (const UniformScaling< Scalar > &s) const

internal::rotation_base_generic_product_selector < Quaternion< _Scalar, _Options >, OtherDerived, OtherDerived::IsVectorAtCompileTime > ::ReturnType	operator* (const EigenBase< OtherDerived > &e) const

Transform< Scalar, Dim, Mode >	operator* (const Transform< Scalar, Dim, Mode, Options > &t) const

	Quaternion ()

	Quaternion (const Scalar &w, const Scalar &x, const Scalar &y, const Scalar &z)

	Quaternion (const Scalar *data)

template<class Derived >
	Quaternion (const QuaternionBase< Derived > &other)

	Quaternion (const AngleAxisType &aa)

template<typename Derived >
	Quaternion (const MatrixBase< Derived > &other)

template<typename OtherScalar , int OtherOptions>
	Quaternion (const Quaternion< OtherScalar, OtherOptions > &other)

Quaternion< _Scalar, _Options > &	setFromTwoVectors (const MatrixBase< Derived1 > &a, const MatrixBase< Derived2 > &b)

QuaternionBase &	setIdentity ()

Scalar	squaredNorm () const

Matrix3	toRotationMatrix () const

const VectorBlock< const Coefficients, 3 >	vec () const

VectorBlock< Coefficients, 3 >	vec ()

Scalar	w () const

Scalar &	w ()

Scalar	x () const

Scalar &	x ()

Scalar	y () const

Scalar &	y ()

Scalar	z () const

Scalar &	z ()

Static Public Member Functions
static Quaternion< Scalar >	Identity ()

Member Typedef Documentation

typedef Matrix<Scalar,3,3> Matrix3

inherited

the equivalent rotation matrix type

typedef Matrix<Scalar,Dim,Dim> RotationMatrixType

inherited

corresponding linear transformation matrix type

typedef Matrix<Scalar,3,1> Vector3

inherited

the type of a 3D vector

Constructor & Destructor Documentation

Quaternion ( )

inline

Default constructor leaving the quaternion uninitialized.

Quaternion	(	const Scalar &	w,
		const Scalar &	x,
		const Scalar &	y,
		const Scalar &	z
	)

inline

Constructs and initializes the quaternion 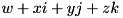$ w+xi+yj+zk $ from its four coefficients w, x, y and z.

Warning: Note the order of the arguments: the real w coefficient first, while internally the coefficients are stored in the following order: [x, y, z, w]

Quaternion ( const Scalar * data )

inline

Constructs and initialize a quaternion from the array data

Quaternion ( const QuaternionBase< Derived > & other )

inline

Copy constructor

Quaternion ( const AngleAxisType & aa )

inlineexplicit

Constructs and initializes a quaternion from the angle-axis aa

Quaternion ( const MatrixBase< Derived > & other )

inlineexplicit

Constructs and initializes a quaternion from either:

a rotation matrix expression,
a 4D vector expression representing quaternion coefficients.

Quaternion ( const Quaternion< OtherScalar, OtherOptions > & other )

inlineexplicit

Explicit copy constructor with scalar conversion

Member Function Documentation

Vector3 _transformVector ( const Vector3 & v ) const

inlineinherited

return the result vector of v through the rotation

Rotation of a vector by a quaternion.

Remarks

If the quaternion is used to rotate several points (>1) then it is much more efficient to first convert it to a 3x3 Matrix. Comparison of the operation cost for n transformations:

Quaternion2: 30n
Via a Matrix3: 24 + 15n

internal::cast_return_type<Quaternion< _Scalar, _Options > ,Quaternion<NewScalarType> >::type cast ( ) const

inlineinherited

Returns: *this with scalar type casted to NewScalarType

Note that if NewScalarType is equal to the current scalar type of *this then this function smartly returns a const reference to *this.

Quaternion<Scalar> conjugate ( ) const

inherited

Returns: the conjugated quaternion; the conjugate of the *this which is equal to the multiplicative inverse if the quaternion is normalized. The conjugate of a quaternion represents the opposite rotation.

See Also: Quaternion2::inverse()

Scalar dot ( const QuaternionBase< OtherDerived > & other ) const

inlineinherited

Returns: the dot product of *this and other Geometrically speaking, the dot product of two unit quaternions corresponds to the cosine of half the angle between the two rotations.

See Also: angularDistance()

References QuaternionBase< Derived >::coeffs().

Quaternion<Scalar,Options> FromTwoVectors	(	const MatrixBase< Derived1 > &	a,
		const MatrixBase< Derived2 > &	b
	)

Returns a quaternion representing a rotation between the two arbitrary vectors a and b. In other words, the built rotation represent a rotation sending the line of direction a to the line of direction b, both lines passing through the origin.

Returns: resulting quaternion

Note that the two input vectors do not have to be normalized, and do not need to have the same norm.

static Quaternion<Scalar> Identity ( )

inlinestaticinherited

Returns: a quaternion representing an identity rotation

See Also: MatrixBase::Identity()

Quaternion<Scalar> inverse ( ) const

inherited

Returns: the quaternion describing the inverse rotation; the multiplicative inverse of *this Note that in most cases, i.e., if you simply want the opposite rotation, and/or the quaternion is normalized, then it is enough to use the conjugate.

See Also: QuaternionBase::conjugate()

bool isApprox	(	const QuaternionBase< OtherDerived > &	other,
		const RealScalar &	prec = `NumTraits<Scalar>::dummy_precision()`
	)		const

inlineinherited

Returns: true if *this is approximately equal to other, within the precision determined by prec.

See Also: MatrixBase::isApprox()

References QuaternionBase< Derived >::coeffs().

RotationMatrixType matrix ( ) const

inlineinherited

Returns: an equivalent rotation matrix This function is added to be conform with the Transform class' naming scheme.

Scalar norm ( ) const

inlineinherited

Returns: the norm of the quaternion's coefficients

See Also: QuaternionBase::squaredNorm(), MatrixBase::norm()

References QuaternionBase< Derived >::coeffs().

void normalize ( void )

inlineinherited

Normalizes the quaternion *this

See Also: normalized(), MatrixBase::normalize()

References QuaternionBase< Derived >::coeffs().

Quaternion<Scalar> normalized ( ) const

inlineinherited

Returns: a normalized copy of *this

See Also: normalize(), MatrixBase::normalized()

References QuaternionBase< Derived >::coeffs().

Transform<Scalar,Dim,Isometry> operator* ( const Translation< Scalar, Dim > & t ) const

inlineinherited

Returns: the concatenation of the rotation *this with a translation t

RotationMatrixType operator* ( const UniformScaling< Scalar > & s ) const

inlineinherited

Returns: the concatenation of the rotation *this with a uniform scaling s

internal::rotation_base_generic_product_selector<Quaternion< _Scalar, _Options > ,OtherDerived,OtherDerived::IsVectorAtCompileTime>::ReturnType operator* ( const EigenBase< OtherDerived > & e ) const

inlineinherited

Returns

the concatenation of the rotation *this with a generic expression e e can be:

a DimxDim linear transformation matrix
a DimxDim diagonal matrix (axis aligned scaling)
a vector of size Dim

Transform<Scalar,Dim,Mode> operator* ( const Transform< Scalar, Dim, Mode, Options > & t ) const

inlineinherited

Returns: the concatenation of the rotation *this with a transformation t

Quaternion< _Scalar, _Options > & setFromTwoVectors	(	const MatrixBase< Derived1 > &	a,
		const MatrixBase< Derived2 > &	b
	)

inherited

Returns: the quaternion which transform a into b through a rotation

Sets *this to be a quaternion representing a rotation between the two arbitrary vectors a and b. In other words, the built rotation represent a rotation sending the line of direction a to the line of direction b, both lines passing through the origin.

Returns: a reference to *this.

Note that the two input vectors do not have to be normalized, and do not need to have the same norm.

QuaternionBase& setIdentity ( )

inlineinherited

See Also: QuaternionBase::Identity(), MatrixBase::setIdentity()

References QuaternionBase< Derived >::coeffs().

Scalar squaredNorm ( ) const

inlineinherited

Returns: the squared norm of the quaternion's coefficients

See Also: QuaternionBase::norm(), MatrixBase::squaredNorm()

References QuaternionBase< Derived >::coeffs().

Matrix3 toRotationMatrix ( void ) const

inherited

Returns: an equivalent 3x3 rotation matrix

Convert the quaternion to a 3x3 rotation matrix. The quaternion is required to be normalized, otherwise the result is undefined.

const VectorBlock<const Coefficients,3> vec ( ) const

inlineinherited

Returns: a read-only vector expression of the imaginary part (x,y,z)

References QuaternionBase< Derived >::coeffs().

VectorBlock<Coefficients,3> vec ( )

inlineinherited

Returns: a vector expression of the imaginary part (x,y,z)

References QuaternionBase< Derived >::coeffs().

Scalar w ( ) const

inlineinherited

Returns: the w coefficient

Scalar& w ( )

inlineinherited

Returns: a reference to the w coefficient

Scalar x ( ) const

inlineinherited

Returns: the x coefficient

Scalar& x ( )

inlineinherited

Returns: a reference to the x coefficient

Scalar y ( ) const

inlineinherited

Returns: the y coefficient

Scalar& y ( )

inlineinherited

Returns: a reference to the y coefficient

Scalar z ( ) const

inlineinherited

Returns: the z coefficient

Scalar& z ( )

inlineinherited

Returns: a reference to the z coefficient

The documentation for this class was generated from the following files:

Detailed Description

template<typename Scalar, int Options = AutoAlign> class Eigen::Quaternion< Scalar, Options >

Public Types

Public Member Functions

Static Public Member Functions

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

template<typename Scalar, int Options = AutoAlign>
class Eigen::Quaternion< Scalar, Options >