| Step | Hyp | Ref
| Expression |
|---|
| 1 | | bnj1000.2 |
. 2
  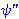 
    ![]. ].](_drbrack.gif)   |
| 2 | | df-ral 2917 |
. . . . 5
    
   
            
              
            
                          |
| 3 | 2 | bicomi 214 |
. . . 4
             
    
                     
        
    
                     |
| 4 | 3 | sbcbii 3491 |
. . 3
      ![]. ].](_drbrack.gif)            
    
                     
    ![]. ].](_drbrack.gif)         
    
                     |
| 5 | | bnj1000.3 |
. . . . . . 7
    |
| 6 | | nfv 1843 |
. . . . . . . 8
      |
| 7 | 6 | sbc19.21g 3502 |
. . . . . . 7
        
  ![]. ].](_drbrack.gif)           
                         
    
    ![]. ].](_drbrack.gif)     
    
                       |
| 8 | 5, 7 | ax-mp 5 |
. . . . . 6
      ![]. ].](_drbrack.gif)                     
                         ![]. ].](_drbrack.gif)      
                          |
| 9 | | nfv 1843 |
. . . . . . . . . 10
       |
| 10 | 9 | sbc19.21g 3502 |
. . . . . . . . 9
        
  ![]. ].](_drbrack.gif)      
                             
     ![]. ].](_drbrack.gif)                           |
| 11 | 5, 10 | ax-mp 5 |
. . . . . . . 8
      ![]. ].](_drbrack.gif)   
            
              
   
      ![]. ].](_drbrack.gif)          
               |
| 12 | | fveq1 6190 |
. . . . . . . . . . 11
                    |
| 13 | | fveq1 6190 |
. . . . . . . . . . . 12
                  |
| 14 | | ax-5 1839 |
. . . . . . . . . . . . 13
             
      |
| 15 | | bnj1000.16 |
. . . . . . . . . . . . . . . 16
              |
| 16 | | nfcv 2764 |
. . . . . . . . . . . . . . . . 17
    |
| 17 | | nfcv 2764 |
. . . . . . . . . . . . . . . . . . 19
    |
| 18 | | bnj1000.15 |
. . . . . . . . . . . . . . . . . . . 20
                   |
| 19 | | nfiu1 4550 |
. . . . . . . . . . . . . . . . . . . 20
    
              |
| 20 | 18, 19 | nfcxfr 2762 |
. . . . . . . . . . . . . . . . . . 19
    |
| 21 | 17, 20 | nfop 4418 |
. . . . . . . . . . . . . . . . . 18
        |
| 22 | 21 | nfsn 4242 |
. . . . . . . . . . . . . . . . 17
          |
| 23 | 16, 22 | nfun 3769 |
. . . . . . . . . . . . . . . 16
              |
| 24 | 15, 23 | nfcxfr 2762 |
. . . . . . . . . . . . . . 15
    |
| 25 | | nfcv 2764 |
. . . . . . . . . . . . . . 15
    |
| 26 | 24, 25 | nffv 6198 |
. . . . . . . . . . . . . 14
        |
| 27 | 26 | nfcrii 2757 |
. . . . . . . . . . . . 13
             
      |
| 28 | 14, 27 | bnj1316 30891 |
. . . . . . . . . . . 12
                                                |
| 29 | 13, 28 | syl 17 |
. . . . . . . . . . 11
                                        |
| 30 | 12, 29 | eqeq12d 2637 |
. . . . . . . . . 10
                
             
                         |
| 31 | | fveq1 6190 |
. . . . . . . . . . 11
                    |
| 32 | | fveq1 6190 |
. . . . . . . . . . . 12
                  |
| 33 | | ax-5 1839 |
. . . . . . . . . . . . 13
                            |
| 34 | 33 | bnj956 30847 |
. . . . . . . . . . . 12
                                                |
| 35 | 32, 34 | syl 17 |
. . . . . . . . . . 11
                                        |
| 36 | 31, 35 | eqeq12d 2637 |
. . . . . . . . . 10
                
             
                         |
| 37 | | fveq1 6190 |
. . . . . . . . . . 11
                    |
| 38 | | fveq1 6190 |
. . . . . . . . . . . 12
                  |
| 39 | | ax-5 1839 |
. . . . . . . . . . . . 13
             
      |
| 40 | 39, 27 | bnj1316 30891 |
. . . . . . . . . . . 12
                                                |
| 41 | 38, 40 | syl 17 |
. . . . . . . . . . 11
                                        |
| 42 | 37, 41 | eqeq12d 2637 |
. . . . . . . . . 10
                
             
                         |
| 43 | 5, 30, 36, 42 | bnj610 30817 |
. . . . . . . . 9
      ![]. ].](_drbrack.gif)                                  
              |
| 44 | 43 | imbi2i 326 |
. . . . . . . 8
            ![]. ].](_drbrack.gif)          
              
   
                           |
| 45 | 11, 44 | bitri 264 |
. . . . . . 7
      ![]. ].](_drbrack.gif)   
            
              
   
                           |
| 46 | 45 | imbi2i 326 |
. . . . . 6
           ![]. ].](_drbrack.gif)                
                          
                          |
| 47 | 8, 46 | bitri 264 |
. . . . 5
      ![]. ].](_drbrack.gif)                     
                          
                          |
| 48 | 47 | albii 1747 |
. . . 4
        ![]. ].](_drbrack.gif)           
                         
            
                          |
| 49 | | sbcal 3485 |
. . . 4
      ![]. ].](_drbrack.gif)            
    
                     
   
  ![]. ].](_drbrack.gif)           
                          |
| 50 | | df-ral 2917 |
. . . 4
    
   
            
              
            
                          |
| 51 | 48, 49, 50 | 3bitr4ri 293 |
. . 3
    
   
            
              
    ![]. ].](_drbrack.gif)                       
                |
| 52 | | bnj1000.1 |
. . . 4
          
            
               |
| 53 | 52 | sbcbii 3491 |
. . 3
      ![]. ].](_drbrack.gif)       ![]. ].](_drbrack.gif)  
                 
               |
| 54 | 4, 51, 53 | 3bitr4ri 293 |
. 2
      ![]. ].](_drbrack.gif)         
            
               |
| 55 | 1, 54 | bitri 264 |
1
  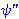 
        
    
                     |