| Step | Hyp | Ref
| Expression |
|---|
| 1 | | bnj1463.18 |
. . . . . . 7
    
   |
| 2 | 1 | elexd 3214 |
. . . . . 6
    
   |
| 3 | | eleq1 2689 |
. . . . . . . 8
          
     |
| 4 | | fneq2 5980 |
. . . . . . . . 9
        
 
     |
| 5 | | raleq 3138 |
. . . . . . . . 9
        
             
   
             |
| 6 | 4, 5 | anbi12d 747 |
. . . . . . . 8
                                                    |
| 7 | 3, 6 | anbi12d 747 |
. . . . . . 7
                                               
                |
| 8 | | bnj1463.1 |
. . . . . . . . . . . 12
        
                  |
| 9 | 8 | bnj1317 30892 |
. . . . . . . . . . 11
         
  |
| 10 | 9 | nfcii 2755 |
. . . . . . . . . 10
    |
| 11 | 10 | nfel2 2781 |
. . . . . . . . 9
      |
| 12 | | bnj1463.2 |
. . . . . . . . . . . . 13
                   |
| 13 | | bnj1463.3 |
. . . . . . . . . . . . 13
        
                       |
| 14 | | bnj1463.4 |
. . . . . . . . . . . . 13
          
      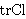           |
| 15 | | bnj1463.5 |
. . . . . . . . . . . . 13
             |
| 16 | | bnj1463.6 |
. . . . . . . . . . . . 13
      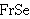
       |
| 17 | | bnj1463.7 |
. . . . . . . . . . . . 13
              
      |
| 18 | | bnj1463.8 |
. . . . . . . . . . . . 13
  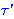      ![]. ].](_drbrack.gif)   |
| 19 | | bnj1463.9 |
. . . . . . . . . . . . 13
        
        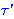  |
| 20 | | bnj1463.10 |
. . . . . . . . . . . . 13
     |
| 21 | | bnj1463.11 |
. . . . . . . . . . . . 13
                   |
| 22 | | bnj1463.12 |
. . . . . . . . . . . . 13
                  |
| 23 | 8, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 | bnj1467 31122 |
. . . . . . . . . . . 12
         
  |
| 24 | 23 | nfcii 2755 |
. . . . . . . . . . 11
    |
| 25 | | nfcv 2764 |
. . . . . . . . . . 11
    |
| 26 | 24, 25 | nffn 5987 |
. . . . . . . . . 10
      |
| 27 | | bnj1463.13 |
. . . . . . . . . . . . 13
                   |
| 28 | 8, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 27 | bnj1446 31113 |
. . . . . . . . . . . 12
                            |
| 29 | 28 | nf5i 2024 |
. . . . . . . . . . 11
              |
| 30 | 25, 29 | nfral 2945 |
. . . . . . . . . 10
                  |
| 31 | 26, 30 | nfan 1828 |
. . . . . . . . 9
                        |
| 32 | 11, 31 | nfan 1828 |
. . . . . . . 8
                              |
| 33 | 32 | nf5ri 2065 |
. . . . . . 7
        
                              
                    |
| 34 | | bnj1463.17 |
. . . . . . . 8
    
   |
| 35 | | bnj1463.16 |
. . . . . . . 8
                    |
| 36 | 1, 34, 35 | jca32 558 |
. . . . . . 7
                                |
| 37 | 7, 33, 36 | bnj1465 30915 |
. . . . . 6
                                        |
| 38 | 2, 37 | mpdan 702 |
. . . . 5
             
                    |
| 39 | | df-rex 2918 |
. . . . 5
                           
                              |
| 40 | 38, 39 | sylibr 224 |
. . . 4
         
                    |
| 41 | | bnj1463.15 |
. . . . 5
    
   |
| 42 | | nfcv 2764 |
. . . . . . . 8
    |
| 43 | 8, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 | bnj1466 31121 |
. . . . . . . . . . 11
         
  |
| 44 | 43 | nfcii 2755 |
. . . . . . . . . 10
    |
| 45 | | nfcv 2764 |
. . . . . . . . . 10
    |
| 46 | 44, 45 | nffn 5987 |
. . . . . . . . 9
      |
| 47 | 8, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 27 | bnj1448 31115 |
. . . . . . . . . . 11
                            |
| 48 | 47 | nf5i 2024 |
. . . . . . . . . 10
              |
| 49 | 45, 48 | nfral 2945 |
. . . . . . . . 9
                  |
| 50 | 46, 49 | nfan 1828 |
. . . . . . . 8
                        |
| 51 | 42, 50 | nfrex 3007 |
. . . . . . 7
        
                   |
| 52 | 51 | nf5ri 2065 |
. . . . . 6
                                                        |
| 53 | 24 | nfeq2 2780 |
. . . . . . 7
      |
| 54 | | fneq1 5979 |
. . . . . . . 8
          
     |
| 55 | | fveq1 6190 |
. . . . . . . . . 10
                  |
| 56 | | reseq1 5390 |
. . . . . . . . . . . . 13
                                |
| 57 | 56 | opeq2d 4409 |
. . . . . . . . . . . 12
                            
           |
| 58 | 57, 27 | syl6eqr 2674 |
. . . . . . . . . . 11
                         |
| 59 | 58 | fveq2d 6195 |
. . . . . . . . . 10
                                 |
| 60 | 55, 59 | eqeq12d 2637 |
. . . . . . . . 9
                     
                         |
| 61 | 60 | ralbidv 2986 |
. . . . . . . 8
        
                
                             |
| 62 | 54, 61 | anbi12d 747 |
. . . . . . 7
                              
                                    |
| 63 | 53, 62 | rexbid 3051 |
. . . . . 6
        
                         
                  
                     |
| 64 | 52, 63, 43 | bnj1468 30916 |
. . . . 5
        
  ![]. ].](_drbrack.gif)                            
                  
                     |
| 65 | 41, 64 | syl 17 |
. . . 4
         ![]. ].](_drbrack.gif)             
                           
   
   
    
              |
| 66 | 40, 65 | mpbird 247 |
. . 3
        ![]. ].](_drbrack.gif)                            
             |
| 67 | | fveq2 6191 |
. . . . . . . 8
                  |
| 68 | | id 22 |
. . . . . . . . . . 11
          |
| 69 | | bnj602 30985 |
. . . . . . . . . . . 12
                        |
| 70 | 69 | reseq2d 5396 |
. . . . . . . . . . 11
                                |
| 71 | 68, 70 | opeq12d 4410 |
. . . . . . . . . 10
                            
           |
| 72 | 12, 71 | syl5eq 2668 |
. . . . . . . . 9
             
           |
| 73 | 72 | fveq2d 6195 |
. . . . . . . 8
                                 |
| 74 | 67, 73 | eqeq12d 2637 |
. . . . . . 7
                  
                            |
| 75 | 74 | cbvralv 3171 |
. . . . . 6
    
            
   
                           |
| 76 | 75 | anbi2i 730 |
. . . . 5
                       
   
    
                            |
| 77 | 76 | rexbii 3041 |
. . . 4
                           
   
   
    
                            |
| 78 | 77 | sbcbii 3491 |
. . 3
      ![]. ].](_drbrack.gif)   
                      
    ![]. ].](_drbrack.gif)             
                            |
| 79 | 66, 78 | sylibr 224 |
. 2
        ![]. ].](_drbrack.gif)                           |
| 80 | 13 | bnj1454 30912 |
. . 3
        
 
    ![]. ].](_drbrack.gif)             
              |
| 81 | 41, 80 | syl 17 |
. 2
             ![]. ].](_drbrack.gif)  
                         |
| 82 | 79, 81 | mpbird 247 |
1
    
   |