Description: Define a class
setrecs   by transfinite recursion, where by transfinite recursion, where
     is
the set of new elements to add to the class given the
set is
the set of new elements to add to the class given the
set  of elements
in the class so far. We do not need a base case,
because we can start with the empty set, which is vacuously a subset of
setrecs of elements
in the class so far. We do not need a base case,
because we can start with the empty set, which is vacuously a subset of
setrecs   . The goal of this definition is to construct a
class
fulfilling theorems setrec1 42438 and setrec2v 42443, which give a more
intuitive idea of the meaning of setrecs. Unlike wrecs,
setrecs is well-defined for any . The goal of this definition is to construct a
class
fulfilling theorems setrec1 42438 and setrec2v 42443, which give a more
intuitive idea of the meaning of setrecs. Unlike wrecs,
setrecs is well-defined for any  and meaningful for any
function and meaningful for any
function  . .
For example, see theorem onsetrec 42451 for how the class  is defined
recursively using the successor function. is defined
recursively using the successor function.
The definition works by building subsets of the desired class and taking
the union of those subsets. To find such a collection of subsets,
consider an arbitrary set  , and consider the result when applying , and consider the result when applying
 to any subset to any subset
   . Remember that . Remember that  can be any
function, and in general we are interested in functions that give
outputs that are larger than their inputs, so we have no reason to
expect the outputs to be within can be any
function, and in general we are interested in functions that give
outputs that are larger than their inputs, so we have no reason to
expect the outputs to be within  . However, if we restrict the
domain of . However, if we restrict the
domain of  to a
given set to a
given set  , the
resulting range will be a
set. Therefore, with this restricted , the
resulting range will be a
set. Therefore, with this restricted  , it makes sense to consider
sets , it makes sense to consider
sets  that are
closed under that are
closed under  applied
to its subsets. Now we
can test whether a given set applied
to its subsets. Now we
can test whether a given set  is recursively generated by is recursively generated by  .
If every set .
If every set  that is closed under
that is closed under  contains
contains  , that
means that every member of , that
means that every member of  must eventually be generated by must eventually be generated by  .
On the other hand, if some such .
On the other hand, if some such  does not contain a certain element
of does not contain a certain element
of  , then that
element can be avoided even if we apply , then that
element can be avoided even if we apply  in
every possible way to previously generated elements. in
every possible way to previously generated elements.
Note that such an omitted element might be eventually recursively
generated by  ,
but not through the elements of ,
but not through the elements of  . In this
case, . In this
case,  would fail
the condition in the definition, but the omitted
element would still be included in some larger would fail
the condition in the definition, but the omitted
element would still be included in some larger  . For example, if . For example, if
 is the
successor function, the set is the
successor function, the set    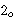  would fail the
condition since would fail the
condition since 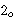 is not an element of the successor of is not an element of the successor of  or or
   . Remember that we are
applying . Remember that we are
applying  to subsets
of to subsets
of  ,
not elements of ,
not elements of  .
In fact, even the set .
In fact, even the set    fails the
condition, since the only subset of previously generated elements is fails the
condition, since the only subset of previously generated elements is
 ,
and ,
and 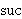  does not have does not have
 as an element.
However,
we can let as an element.
However,
we can let  be
any ordinal, since each of its elements is generated
by starting with be
any ordinal, since each of its elements is generated
by starting with  and repeatedly applying the successor function. and repeatedly applying the successor function.
A similar definition I initially used for setrecs   was
setrecs was
setrecs      recs recs               .
I had initially tried and failed to find an elementary definition, and I
had proven theorems analogous to setrec1 42438 and setrec2v 42443 using the old
definition before I found the new one. I decided to change definitions
for two reasons. First, as John Conway noted in the Appendix to Part
Zero of ONAG, mathematicians should not be caught up in any particular
formalization, such as ZF set theory. Instead, they should work under
whatever framework best suits the problem, and the formal bases used for
different problems can be shown to be equivalent. Thus, Conway
preferred defining surreal numbers as equivalence classes of surreal
number forms, rather than sign-expansions. Although sign-expansions are
easier to implement in ZF set theory, Conway argued that
"formalisation
within some particular axiomatic set theory is irrelevant."
Furthermore, one of the most remarkable properties of the theory of
surreal numbers is that it generates so much from almost nothing. Using
sign-expansions as the formal definition destroys the beauty of surreal
numbers, because ordinals are already built in. For this reason, I
replaced the old definition of setrecs, which also relied heavily
on ordinal numbers. On the other hand, both surreal numbers and the
elementary definition of setrecs immediately generate the ordinal
numbers from a (relatively) very simple set-theoretical basis. .
I had initially tried and failed to find an elementary definition, and I
had proven theorems analogous to setrec1 42438 and setrec2v 42443 using the old
definition before I found the new one. I decided to change definitions
for two reasons. First, as John Conway noted in the Appendix to Part
Zero of ONAG, mathematicians should not be caught up in any particular
formalization, such as ZF set theory. Instead, they should work under
whatever framework best suits the problem, and the formal bases used for
different problems can be shown to be equivalent. Thus, Conway
preferred defining surreal numbers as equivalence classes of surreal
number forms, rather than sign-expansions. Although sign-expansions are
easier to implement in ZF set theory, Conway argued that
"formalisation
within some particular axiomatic set theory is irrelevant."
Furthermore, one of the most remarkable properties of the theory of
surreal numbers is that it generates so much from almost nothing. Using
sign-expansions as the formal definition destroys the beauty of surreal
numbers, because ordinals are already built in. For this reason, I
replaced the old definition of setrecs, which also relied heavily
on ordinal numbers. On the other hand, both surreal numbers and the
elementary definition of setrecs immediately generate the ordinal
numbers from a (relatively) very simple set-theoretical basis.
Second, although it is still complicated to formalize the theory of
recursively generated sets within ZF set theory, it is actually simpler
and more natural to do so with set theory directly than with the theory
of ordinal numbers. As Conway wrote, indexing the "birthdays"
of sets
is and should be unnecessary. Using an elementary definition for
setrecs removes the reliance on the previously developed theory of
ordinal numbers, allowing proofs to be simpler and more direct.
Formalizing surreal numbers within metamath is probably still not in the
spirit of Conway. He said that "attempts to force arbitrary
theories
into a single formal straitjacket... produce unnecessarily cumbrous and
inelegant contortions." Nevertheless, metamath has proven to be
much
more versatile than it seems at first, and I think the theory of surreal
numbers can be natural while fitting well into the metamath framework.
The difficulty in writing a definition in metamath for setrecs   is that the necessary properties to prove are self-referential (see
setrec1 42438 and setrec2v 42443), so we cannot simply write the properties
we
want inside a class abstraction as with most definitions. As noted in
the comment of df-rdg 7506, this is not actually a requirement of the
metamath language, but we would like to be able to eliminate all
definitions by direct mechanical substitution.
is that the necessary properties to prove are self-referential (see
setrec1 42438 and setrec2v 42443), so we cannot simply write the properties
we
want inside a class abstraction as with most definitions. As noted in
the comment of df-rdg 7506, this is not actually a requirement of the
metamath language, but we would like to be able to eliminate all
definitions by direct mechanical substitution.
We cannot define setrecs using a class abstraction directly, because
nothing about its individual elements tells us whether they are in the
set. We need to know about previous elements first. One way of getting
around this problem without indexing is by defining setrecs   as
a union or intersection of suitable sets. Thus, instead of using a
class abstraction for the elements of setrecs as
a union or intersection of suitable sets. Thus, instead of using a
class abstraction for the elements of setrecs   , which seems
to
be impossible, we can use a class abstraction for supersets or subsets
of setrecs , which seems
to
be impossible, we can use a class abstraction for supersets or subsets
of setrecs   , which "know" about multiple individual
elements
at a time. , which "know" about multiple individual
elements
at a time.
Note that we cannot define setrecs   as an
intersection of sets,
because in general it is a proper class, so any supersets would also be
proper classes. However, a proper class can be a union of sets, as long
as the collection of such sets is a proper class. Therefore, it is
feasible to define setrecs as an
intersection of sets,
because in general it is a proper class, so any supersets would also be
proper classes. However, a proper class can be a union of sets, as long
as the collection of such sets is a proper class. Therefore, it is
feasible to define setrecs   as a union of a class
abstraction. as a union of a class
abstraction.
If setrecs      , the elements of A must be
subsets of
setrecs , the elements of A must be
subsets of
setrecs   which together include everything recursively
generated by which together include everything recursively
generated by  .
We can do this by letting .
We can do this by letting  be the class of
sets be the class of
sets  whose
elements are all recursively generated by whose
elements are all recursively generated by  . .
One necessary condition is that each element of a given    must
be generated by must
be generated by  when applied to a previous element when applied to a previous element    .
In symbols, .
In symbols,      
       
        .
However, this is not sufficient. All fixed points .
However, this is not sufficient. All fixed points  of of  will
satisfy this condition whether they should be in setrecs will
satisfy this condition whether they should be in setrecs   or
not. If we replace the subset relation with the proper subset relation, or
not. If we replace the subset relation with the proper subset relation,
 cannot be the
empty set, even though the empty set should be in cannot be the
empty set, even though the empty set should be in
 . Therefore
this condition cannot be used in the definition, even
if we can find a way to avoid making it circular. . Therefore
this condition cannot be used in the definition, even
if we can find a way to avoid making it circular.
A better strategy is to find a necessary and sufficient condition for
all the elements of a set    to be generated by to be generated by  when
applied only to sets of previously generated elements within when
applied only to sets of previously generated elements within  .
For example, taking .
For example, taking  to be the successor function, we can let to be the successor function, we can let
   rather than rather than   , and we will still have , and we will still have  
  as required. This gets rid of the circularity of the definition, since
we should have a condition to test whether a given set
as required. This gets rid of the circularity of the definition, since
we should have a condition to test whether a given set  is in is in  without knowing about any of the other elements of
without knowing about any of the other elements of  . .
The definition I ended up using accomplishes this using induction:  is defined as the class of sets
is defined as the class of sets  for which a sort of induction on
the elements of for which a sort of induction on
the elements of  holds. However, when creating a definition for
setrecs that did not rely on ordinal numbers, I tried at first to
write a definition using the well-founded relation predicate,
holds. However, when creating a definition for
setrecs that did not rely on ordinal numbers, I tried at first to
write a definition using the well-founded relation predicate, 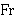 .
I thought that this would be simple to do once I found a suitable
definition using induction, just as the least- element principle is
equivalent to induction on the positive integers. If we let .
I thought that this would be simple to do once I found a suitable
definition using induction, just as the least- element principle is
equivalent to induction on the positive integers. If we let
   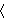    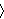          , then , then
  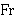        
     
                   . .
On 22-Jul-2020 I came up with the following definition (Version 1)
phrased in terms of induction:      
                           
In Aug-2020 I came up with an equivalent definition with the goal of
phrasing it in terms of the relation 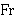 . It is the contrapositive
of the previous one with . It is the contrapositive
of the previous one with  replaced by its complement. replaced by its complement.
     
   
                 
    
These definitions didn't work because the induction didn't "get off
the
ground." If  does not contain the empty set, the condition does not contain the empty set, the condition
    
  fails, so fails, so    doesn't get included in
doesn't get included in
 even though it
should. This could be fixed by adding the base
case as a separate requirement, but the subtler problem would remain
that rather than a set of "acceptable" sets, what we really
need is a
collection even though it
should. This could be fixed by adding the base
case as a separate requirement, but the subtler problem would remain
that rather than a set of "acceptable" sets, what we really
need is a
collection  of
all individuals that have been generated so far. So
one approach is to replace every occurence of of
all individuals that have been generated so far. So
one approach is to replace every occurence of   with with   ,
making ,
making  a set of
individuals rather than a family of sets. That
solves this problem, but it complicates the foundedness version of the
definition, which looked cleaner in Version 1. a set of
individuals rather than a family of sets. That
solves this problem, but it complicates the foundedness version of the
definition, which looked cleaner in Version 1.
There was another problem with Version 1. If we let  be the power
set function, then the induction in the inductive version works for be the power
set function, then the induction in the inductive version works for
 being the class
of transitive sets, restricted to subsets of being the class
of transitive sets, restricted to subsets of
 . Therefore, . Therefore,
 must be transitive by
definition of must be transitive by
definition of  .
This doesn't affect the union of all such .
This doesn't affect the union of all such  , but it may or may not
be desirable. The problem is that , but it may or may not
be desirable. The problem is that  is only applied to transitive
sets, because of the strong requirement is only applied to transitive
sets, because of the strong requirement    , so the
definition
requires the additional constraint , so the
definition
requires the additional constraint        a ) C_ ( F a ) C_ ( F
   in order to work. This issue can also be avoided by replacing in order to work. This issue can also be avoided by replacing
  with with   . The induction version of the result is used in
the final definition. . The induction version of the result is used in
the final definition.
Version 2: (18-Aug-2020) Induction:      
                  
   
     Foundedness:
Foundedness:             
    
             
     
In the induction version, not only does  include all the elements
of include all the elements
of  , but it must
include the elements of , but it must
include the elements of      for for
    
  even if those elements of even if those elements of      are not in are not in
 . We shouldn't
care about any of the elements of . We shouldn't
care about any of the elements of  outside outside
 , but this detail
doesn't affect the correctness of the
definition. If we replaced , but this detail
doesn't affect the correctness of the
definition. If we replaced      in the definition by in the definition by
         , we would get
the same class for
setrecs , we would get
the same class for
setrecs   . Suppose we could find a . Suppose we could find a  for which the
condition fails for a given for which the
condition fails for a given  under the changed definition. Then
the antecedent would be true, but under the changed definition. Then
the antecedent would be true, but    would be
false. We could
then simply add all elements of would be
false. We could
then simply add all elements of      outside of outside of  for any for any
   , which we can do because all the classes
involved are sets.
This is not trivial and requires the axioms of union, power set, and
replacement. However, the expanded , which we can do because all the classes
involved are sets.
This is not trivial and requires the axioms of union, power set, and
replacement. However, the expanded  fails the condition under the
metamath definition. The other direction is easier. If a certain fails the condition under the
metamath definition. The other direction is easier. If a certain  fails the metamath definition, then all
fails the metamath definition, then all        for for
    
  , and in particular , and in particular       
    . .
The foundedness version is starting to look more like ax-reg 8497! We
want to take advantage of the preexisting relation 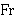 , which seems
closely related to our foundedness definition. Since we only care about
the elements of , which seems
closely related to our foundedness definition. Since we only care about
the elements of  which are subsets of
which are subsets of  ,
we can restrict ,
we can restrict  to
to  in the
foundedness definition. Furthermore, instead of
quantifying over in the
foundedness definition. Furthermore, instead of
quantifying over  , quantify over the elements , quantify over the elements  
 overlapping with
overlapping with  . Versions 3, 4, and 5 are all equivalent to
Version 2. . Versions 3, 4, and 5 are all equivalent to
Version 2.
Version 3 - Foundedness (5-Sep-2020):
            
  
         
                 
Now, if we replace      by by          , we do
not change the definition. We already know that , we do
not change the definition. We already know that    since
since
   and and  
 . All we need to show
in order to prove that
this change leads to an equivalent definition is to find . All we need to show
in order to prove that
this change leads to an equivalent definition is to find
To make our definition look exactly like df-fr 5073, we add another
variable 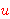 representing the nonexistent element of
representing the nonexistent element of  in in  . .
Version 4 - Foundedness (6-Sep-2020):
            
   
       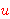 
   
   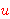
   
      
This is so close to df-fr 5073; the only change needed is to switch
  with with  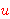 
 . Unfortunately, I
couldn't find any way to
switch the quantifiers without interfering with the definition. Maybe
there is a definition equivalent to this one that uses . Unfortunately, I
couldn't find any way to
switch the quantifiers without interfering with the definition. Maybe
there is a definition equivalent to this one that uses 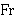 , but I
couldn't find one. Yet, we can still find a remarkable similarity
between Foundedness Version 2 and ax-reg 8497. Rather than a disjoint
element of , but I
couldn't find one. Yet, we can still find a remarkable similarity
between Foundedness Version 2 and ax-reg 8497. Rather than a disjoint
element of  ,
there's a disjoint coverer of an element of ,
there's a disjoint coverer of an element of  . .
Finally, here's a different dead end I followed:
To clean up our foundedness definition, we keep  as a family of
sets as a family of
sets  but allow but allow
 to be any subset of to be any subset of
  in the
induction. With this stronger induction, we can also allow for the
stronger requirement in the
induction. With this stronger induction, we can also allow for the
stronger requirement     rather than only rather than only    .
This
will help improve the foundedness version. .
This
will help improve the foundedness version.
Version 1.1 (28-Aug-2020) Induction:         
    
                 
    Foundedness:
Foundedness:                  
        
               
( Edit (Aug 31) - this isn't true! Nothing forces the subset of an
element of  to be
in to be
in  . Version 2 does not
have this issue. ) . Version 2 does not
have this issue. )
Similarly, we could allow  to be any subset of any element of to be any subset of any element of  rather than any subset of
rather than any subset of   . I
think this has the same problem. . I
think this has the same problem.
We want to take advantage of the preexisting relation 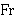 , which
seems closely related to our foundedness definition. Since we only care
about the elements of , which
seems closely related to our foundedness definition. Since we only care
about the elements of  which are subsets of which are subsets of  , we can restrict , we can restrict
 to to   in the foundedness definition: in the foundedness definition:
Version 1.2 (31-Aug-2020) Foundedness:
                
             
           
Now this looks more like df-fr 5073! The last step necessary to be able
to use 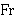 directly in our definition is to replace
directly in our definition is to replace      with its own setvar variable, corresponding to
with its own setvar variable, corresponding to  in df-fr 5073. in df-fr 5073.
This definition is incorrect, though, since there's nothing forcing the
subset of an element of  to be in to be in  . .
Version 1.3 (31-Aug-2020) Induction:             
                      
      Foundedness:
Foundedness:
                        
    
       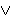           
 must contain the
supersets of each of its elements in the
foundedness version, and we can't make any restrictions on must contain the
supersets of each of its elements in the
foundedness version, and we can't make any restrictions on  or or
 , so this
doesn't work. , so this
doesn't work.
Let's try letting R be the covering relation
   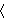    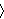  
       to solve the transitivity
issue (i.e. that if to solve the transitivity
issue (i.e. that if  is the power set relation, is the power set relation,  consists only
of transitive sets). The set consists only
of transitive sets). The set      corresponds to the variable corresponds to the variable
 in df-fr 5073. Thus, in our case, df-fr 5073 is equivalent to in df-fr 5073. Thus, in our case, df-fr 5073 is equivalent to
  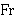        
     
                          .
Substituting our relation .
Substituting our relation  gives gives
  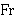        
      
                            
This doesn't work for non-injective  because we need all because we need all  to
be straddlers, but we don't necessarily need all-straddlers; loops
within z are fine for non-injective F. to
be straddlers, but we don't necessarily need all-straddlers; loops
within z are fine for non-injective F.
Consider the foundedness form of Version 1. We want to show
                 so we can replace one with
the other. Negate both sides: so we can replace one with
the other. Negate both sides:  
 
          
If  is
injective, then we should be able to pick a suitable R,
being careful about the above problem for some F (for example z =
transitivity) when changing the antecedent y e. z' to z =/= (/). If
we're clever, we can get rid of the injectivity requirement. The
forward direction of the above equivalence always holds, but the key is
that although the backwards direction doesn't hold in general, we can
always find some z' where it doesn't work for is
injective, then we should be able to pick a suitable R,
being careful about the above problem for some F (for example z =
transitivity) when changing the antecedent y e. z' to z =/= (/). If
we're clever, we can get rid of the injectivity requirement. The
forward direction of the above equivalence always holds, but the key is
that although the backwards direction doesn't hold in general, we can
always find some z' where it doesn't work for  itself. If there
exists a z' where the version with the w condition fails, then there
exists a z' where the version with the v condition also fails. However,
Version 1 is not a correct definition, so this doesn't work either.
(Contributed by Emmett Weisz, 18-Aug-2020.)
(New usage is discouraged.) itself. If there
exists a z' where the version with the w condition fails, then there
exists a z' where the version with the v condition also fails. However,
Version 1 is not a correct definition, so this doesn't work either.
(Contributed by Emmett Weisz, 18-Aug-2020.)
(New usage is discouraged.) |