Theorem List for Metamath Proof Explorer - 42401-42500 *Has distinct variable
group(s)
| Type | Label | Description |
|---|
| Statement |
|---|
| |
| Theorem | digexp 42401 |
The  th digit of a
power to the base is either 1 or 0. (Contributed
by AV, 24-May-2020.) th digit of a
power to the base is either 1 or 0. (Contributed
by AV, 24-May-2020.)
|
      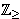      
          digit digit        
   
        |
| |
| Theorem | dig1 42402 |
All but one digits of 1 are 0. (Contributed by AV, 24-May-2020.)
|
      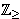      
      digit digit                 |
| |
| Theorem | 0dig1 42403 |
The  th digit of 1 is 1
in any positional system. (Contributed by
AV, 28-May-2020.) th digit of 1 is 1
in any positional system. (Contributed by
AV, 28-May-2020.)
|
   
 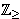   
    digit digit        |
| |
| Theorem | 0dig2pr01 42404 |
The integers 0 and 1 correspond to their last bit. (Contributed by AV,
28-May-2010.)
|
   
         digit digit        |
| |
| Theorem | dig2nn0 42405 |
A digit of a nonnegative integer  in a binary system is either 0 or
1. (Contributed by AV, 24-May-2020.) in a binary system is either 0 or
1. (Contributed by AV, 24-May-2020.)
|
               digit digit            |
| |
| Theorem | 0dig2nn0e 42406 |
The last bit of an even integer is 0. (Contributed by AV, 3-Jun-2010.)
|
                   digit digit        |
| |
| Theorem | 0dig2nn0o 42407 |
The last bit of an odd integer is 1. (Contributed by AV, 3-Jun-2010.)
|
            
          digit digit        |
| |
| Theorem | dig2bits 42408 |
The  th digit of a
nonnegative integer th digit of a
nonnegative integer  in a binary system is
its
in a binary system is
its  th bit.
(Contributed by AV, 24-May-2020.) th bit.
(Contributed by AV, 24-May-2020.)
|
                digit digit        
  bits bits     |
| |
| 20.35.17.11 Nonnegative integer as sum of its
shifted digits
|
| |
| Theorem | dignn0flhalflem1 42409 |
Lemma 1 for dignn0flhalf 42412. (Contributed by AV, 7-Jun-2012.)
|
            
       
    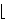        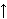          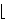       
   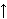      |
| |
| Theorem | dignn0flhalflem2 42410 |
Lemma 2 for dignn0flhalf 42412. (Contributed by AV, 7-Jun-2012.)
|
            
       
    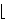       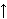           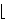    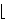           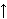      |
| |
| Theorem | dignn0ehalf 42411 |
The digits of the half of an even nonnegative integer are the digits of
the integer shifted by 1. (Contributed by AV, 3-Jun-2010.)
|
                           digit digit         digit digit          |
| |
| Theorem | dignn0flhalf 42412 |
The digits of the rounded half of a nonnegative integer are the digits of
the integer shifted by 1. (Contributed by AV, 7-Jun-2010.)
|
      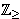      
          digit digit         digit digit    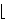          |
| |
| Theorem | nn0sumshdiglemA 42413* |
Lemma for nn0sumshdig 42417 (induction step, even multiplier).
(Contributed
by AV, 3-Jun-2020.)
|
       
                
    #b #b    
    
   ..^ ..^      digit digit        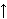        #b #b           
     ..^ ..^          digit digit        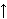       |
| |
| Theorem | nn0sumshdiglemB 42414* |
Lemma for nn0sumshdig 42417 (induction step, odd multiplier).
(Contributed
by AV, 7-Jun-2020.)
|
       
                    
    #b #b    
    
   ..^ ..^      digit digit        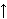        #b #b           
     ..^ ..^          digit digit        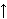       |
| |
| Theorem | nn0sumshdiglem1 42415* |
Lemma 1 for nn0sumshdig 42417 (induction step). (Contributed by AV,
7-Jun-2020.)
|
             #b #b    
    
   ..^ ..^      digit digit        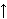            #b #b         
       ..^ ..^          digit digit        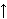       |
| |
| Theorem | nn0sumshdiglem2 42416* |
Lemma 2 for nn0sumshdig 42417. (Contributed by AV, 7-Jun-2020.)
|
   
        #b #b    
    
   ..^ ..^      digit digit        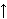      |
| |
| Theorem | nn0sumshdig 42417* |
A nonnegative integer can be represented as sum of its shifted bits.
(Contributed by AV, 7-Jun-2020.)
|
   
         ..^ ..^ #b #b        digit digit        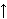     |
| |
| 20.35.17.12 Algorithms for the multiplication
of nonnegative integers
|
| |
| Theorem | nn0mulfsum 42418* |
Trivial algorithm to calculate the product of two nonnegative integers
 and and  by adding up by adding up   times. (Contributed by AV,
17-May-2020.) times. (Contributed by AV,
17-May-2020.)
|
                 
          |
| |
| Theorem | nn0mullong 42419* |
Standard algorithm (also known as "long multiplication" or
"grade-school
multiplication") to calculate the product of two nonnegative
integers
 and and  by multiplying the
multiplicand by multiplying the
multiplicand  by each
digit of
the multiplier by each
digit of
the multiplier  and then add up all the properly shifted results.
Here, the binary representation of the multiplier
and then add up all the properly shifted results.
Here, the binary representation of the multiplier  is used, i.e.
the above mentioned "digits" are 0 or 1. This is a similar
result as
provided by smumul 15215. (Contributed by AV, 7-Jun-2020.) is used, i.e.
the above mentioned "digits" are 0 or 1. This is a similar
result as
provided by smumul 15215. (Contributed by AV, 7-Jun-2020.)
|
                 
     ..^ ..^ #b #b         digit digit        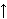        |
| |
| 20.36 Mathbox for Emmett
Weisz
|
| |
| 20.36.1 Miscellaneous Theorems
Some of these theorems are used in the series of lemmas and theorems proving
the defining properties of setrecs.
|
| |
| Theorem | nfintd 42420 |
Bound-variable hypothesis builder for intersection. (Contributed by
Emmett Weisz, 16-Jan-2020.)
|
            
     |
| |
| Theorem | nfiund 42421 |
Bound-variable hypothesis builder for indexed union. (Contributed by
Emmett Weisz, 6-Dec-2019.)
|
 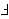                         
  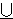  
   |
| |
| Theorem | iunord 42422* |
The indexed union of a collection of ordinal numbers     is
ordinal. This proof is based on the proof of ssorduni 6985, but does not
use it directly, since ssorduni 6985 does not work when is
ordinal. This proof is based on the proof of ssorduni 6985, but does not
use it directly, since ssorduni 6985 does not work when  is a proper
class. (Contributed by Emmett Weisz, 3-Nov-2019.) is a proper
class. (Contributed by Emmett Weisz, 3-Nov-2019.)
|
   
  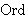  
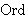 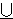      |
| |
| Theorem | iunordi 42423* |
The indexed union of a collection of ordinal numbers     is
ordinal. (Contributed by Emmett Weisz, 3-Nov-2019.) is
ordinal. (Contributed by Emmett Weisz, 3-Nov-2019.)
|
 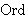    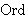 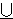 
   |
| |
| Theorem | rspcdf 42424* |
Restricted specialization, using implicit substitution. (Contributed by
Emmett Weisz, 16-Jan-2020.)
|
 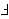     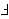                                            |
| |
| Theorem | spd 42425 |
Specialization deduction, using implicit substitution. Based on the
proof of spimed 2255. (Contributed by Emmett Weisz, 17-Jan-2020.)
|
    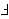                              |
| |
| Theorem | spcdvw 42426* |
A version of spcdv 3291 where  and and  are direct substitutions of
each other. This theorem is useful because it does not require are direct substitutions of
each other. This theorem is useful because it does not require  and
and  to be
distinct variables. (Contributed by Emmett Weisz,
12-Apr-2020.) to be
distinct variables. (Contributed by Emmett Weisz,
12-Apr-2020.)
|
                                  |
| |
| Theorem | tfis2d 42427* |
Transfinite Induction Schema, using implicit substitution. (Contributed
by Emmett Weisz, 3-May-2020.)
|
        
                     
                   |
| |
| Theorem | bnd2d 42428* |
Deduction form of bnd2 8756. (Contributed by Emmett Weisz,
19-Jan-2021.)
|
                                              |
| |
| Theorem | dffun3f 42429* |
Alternate definition of function, using bound-variable hypotheses
instead of distinct variable conditions. (Contributed by Emmett Weisz,
14-Mar-2021.)
|
                 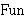    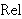              
     |
| |
| 20.36.2 Set Recursion
|
| |
| 20.36.2.1 Basic Properties of Set
Recursion
Symbols in this section:
All the symbols used in the definition of setrecs   are explained
in
the comment of df-setrecs 42431. The class are explained
in
the comment of df-setrecs 42431. The class  is explained in the comment of
setrec1lem1 42434. Glossaries of symbols used in individual
proofs, or used
differently in different proofs, are in the comments of those proofs. is explained in the comment of
setrec1lem1 42434. Glossaries of symbols used in individual
proofs, or used
differently in different proofs, are in the comments of those proofs.
|
| |
| Syntax | csetrecs 42430 |
Extend class notation to include a set defined by transfinite
recursion.
|
 setrecs setrecs   |
| |
| Definition | df-setrecs 42431* |
Define a class setrecs   by transfinite recursion,
where by transfinite recursion,
where
     is
the set of new elements to add to the class given the
set is
the set of new elements to add to the class given the
set  of elements
in the class so far. We do not need a base case,
because we can start with the empty set, which is vacuously a subset of
setrecs of elements
in the class so far. We do not need a base case,
because we can start with the empty set, which is vacuously a subset of
setrecs   . The goal of this definition is to construct a
class
fulfilling theorems setrec1 42438 and setrec2v 42443, which give a more
intuitive idea of the meaning of setrecs. Unlike wrecs,
setrecs is well-defined for any . The goal of this definition is to construct a
class
fulfilling theorems setrec1 42438 and setrec2v 42443, which give a more
intuitive idea of the meaning of setrecs. Unlike wrecs,
setrecs is well-defined for any  and meaningful for any
function and meaningful for any
function  . .
For example, see theorem onsetrec 42451 for how the class  is defined
recursively using the successor function. is defined
recursively using the successor function.
The definition works by building subsets of the desired class and taking
the union of those subsets. To find such a collection of subsets,
consider an arbitrary set  , and consider the result when applying , and consider the result when applying
 to any subset to any subset
   . Remember that . Remember that  can be any
function, and in general we are interested in functions that give
outputs that are larger than their inputs, so we have no reason to
expect the outputs to be within can be any
function, and in general we are interested in functions that give
outputs that are larger than their inputs, so we have no reason to
expect the outputs to be within  . However, if we restrict the
domain of . However, if we restrict the
domain of  to a
given set to a
given set  , the
resulting range will be a
set. Therefore, with this restricted , the
resulting range will be a
set. Therefore, with this restricted  , it makes sense to consider
sets , it makes sense to consider
sets  that are
closed under that are
closed under  applied
to its subsets. Now we
can test whether a given set applied
to its subsets. Now we
can test whether a given set  is recursively generated by is recursively generated by  .
If every set .
If every set  that is closed under
that is closed under  contains
contains  , that
means that every member of , that
means that every member of  must eventually be generated by must eventually be generated by  .
On the other hand, if some such .
On the other hand, if some such  does not contain a certain element
of does not contain a certain element
of  , then that
element can be avoided even if we apply , then that
element can be avoided even if we apply  in
every possible way to previously generated elements. in
every possible way to previously generated elements.
Note that such an omitted element might be eventually recursively
generated by  ,
but not through the elements of ,
but not through the elements of  . In this
case, . In this
case,  would fail
the condition in the definition, but the omitted
element would still be included in some larger would fail
the condition in the definition, but the omitted
element would still be included in some larger  . For example, if . For example, if
 is the
successor function, the set is the
successor function, the set    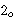  would fail the
condition since would fail the
condition since 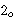 is not an element of the successor of is not an element of the successor of  or or
   . Remember that we are
applying . Remember that we are
applying  to subsets
of to subsets
of  ,
not elements of ,
not elements of  .
In fact, even the set .
In fact, even the set    fails the
condition, since the only subset of previously generated elements is fails the
condition, since the only subset of previously generated elements is
 ,
and ,
and 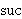  does not have does not have
 as an element.
However,
we can let as an element.
However,
we can let  be
any ordinal, since each of its elements is generated
by starting with be
any ordinal, since each of its elements is generated
by starting with  and repeatedly applying the successor function. and repeatedly applying the successor function.
A similar definition I initially used for setrecs   was
setrecs was
setrecs      recs recs               .
I had initially tried and failed to find an elementary definition, and I
had proven theorems analogous to setrec1 42438 and setrec2v 42443 using the old
definition before I found the new one. I decided to change definitions
for two reasons. First, as John Conway noted in the Appendix to Part
Zero of ONAG, mathematicians should not be caught up in any particular
formalization, such as ZF set theory. Instead, they should work under
whatever framework best suits the problem, and the formal bases used for
different problems can be shown to be equivalent. Thus, Conway
preferred defining surreal numbers as equivalence classes of surreal
number forms, rather than sign-expansions. Although sign-expansions are
easier to implement in ZF set theory, Conway argued that
"formalisation
within some particular axiomatic set theory is irrelevant."
Furthermore, one of the most remarkable properties of the theory of
surreal numbers is that it generates so much from almost nothing. Using
sign-expansions as the formal definition destroys the beauty of surreal
numbers, because ordinals are already built in. For this reason, I
replaced the old definition of setrecs, which also relied heavily
on ordinal numbers. On the other hand, both surreal numbers and the
elementary definition of setrecs immediately generate the ordinal
numbers from a (relatively) very simple set-theoretical basis. .
I had initially tried and failed to find an elementary definition, and I
had proven theorems analogous to setrec1 42438 and setrec2v 42443 using the old
definition before I found the new one. I decided to change definitions
for two reasons. First, as John Conway noted in the Appendix to Part
Zero of ONAG, mathematicians should not be caught up in any particular
formalization, such as ZF set theory. Instead, they should work under
whatever framework best suits the problem, and the formal bases used for
different problems can be shown to be equivalent. Thus, Conway
preferred defining surreal numbers as equivalence classes of surreal
number forms, rather than sign-expansions. Although sign-expansions are
easier to implement in ZF set theory, Conway argued that
"formalisation
within some particular axiomatic set theory is irrelevant."
Furthermore, one of the most remarkable properties of the theory of
surreal numbers is that it generates so much from almost nothing. Using
sign-expansions as the formal definition destroys the beauty of surreal
numbers, because ordinals are already built in. For this reason, I
replaced the old definition of setrecs, which also relied heavily
on ordinal numbers. On the other hand, both surreal numbers and the
elementary definition of setrecs immediately generate the ordinal
numbers from a (relatively) very simple set-theoretical basis.
Second, although it is still complicated to formalize the theory of
recursively generated sets within ZF set theory, it is actually simpler
and more natural to do so with set theory directly than with the theory
of ordinal numbers. As Conway wrote, indexing the "birthdays"
of sets
is and should be unnecessary. Using an elementary definition for
setrecs removes the reliance on the previously developed theory of
ordinal numbers, allowing proofs to be simpler and more direct.
Formalizing surreal numbers within metamath is probably still not in the
spirit of Conway. He said that "attempts to force arbitrary
theories
into a single formal straitjacket... produce unnecessarily cumbrous and
inelegant contortions." Nevertheless, metamath has proven to be
much
more versatile than it seems at first, and I think the theory of surreal
numbers can be natural while fitting well into the metamath framework.
The difficulty in writing a definition in metamath for setrecs   is that the necessary properties to prove are self-referential (see
setrec1 42438 and setrec2v 42443), so we cannot simply write the properties
we
want inside a class abstraction as with most definitions. As noted in
the comment of df-rdg 7506, this is not actually a requirement of the
metamath language, but we would like to be able to eliminate all
definitions by direct mechanical substitution.
is that the necessary properties to prove are self-referential (see
setrec1 42438 and setrec2v 42443), so we cannot simply write the properties
we
want inside a class abstraction as with most definitions. As noted in
the comment of df-rdg 7506, this is not actually a requirement of the
metamath language, but we would like to be able to eliminate all
definitions by direct mechanical substitution.
We cannot define setrecs using a class abstraction directly, because
nothing about its individual elements tells us whether they are in the
set. We need to know about previous elements first. One way of getting
around this problem without indexing is by defining setrecs   as
a union or intersection of suitable sets. Thus, instead of using a
class abstraction for the elements of setrecs as
a union or intersection of suitable sets. Thus, instead of using a
class abstraction for the elements of setrecs   , which seems
to
be impossible, we can use a class abstraction for supersets or subsets
of setrecs , which seems
to
be impossible, we can use a class abstraction for supersets or subsets
of setrecs   , which "know" about multiple individual
elements
at a time. , which "know" about multiple individual
elements
at a time.
Note that we cannot define setrecs   as an
intersection of sets,
because in general it is a proper class, so any supersets would also be
proper classes. However, a proper class can be a union of sets, as long
as the collection of such sets is a proper class. Therefore, it is
feasible to define setrecs as an
intersection of sets,
because in general it is a proper class, so any supersets would also be
proper classes. However, a proper class can be a union of sets, as long
as the collection of such sets is a proper class. Therefore, it is
feasible to define setrecs   as a union of a class
abstraction. as a union of a class
abstraction.
If setrecs      , the elements of A must be
subsets of
setrecs , the elements of A must be
subsets of
setrecs   which together include everything recursively
generated by which together include everything recursively
generated by  .
We can do this by letting .
We can do this by letting  be the class of
sets be the class of
sets  whose
elements are all recursively generated by whose
elements are all recursively generated by  . .
One necessary condition is that each element of a given    must
be generated by must
be generated by  when applied to a previous element when applied to a previous element    .
In symbols, .
In symbols,      
       
        .
However, this is not sufficient. All fixed points .
However, this is not sufficient. All fixed points  of of  will
satisfy this condition whether they should be in setrecs will
satisfy this condition whether they should be in setrecs   or
not. If we replace the subset relation with the proper subset relation, or
not. If we replace the subset relation with the proper subset relation,
 cannot be the
empty set, even though the empty set should be in cannot be the
empty set, even though the empty set should be in
 . Therefore
this condition cannot be used in the definition, even
if we can find a way to avoid making it circular. . Therefore
this condition cannot be used in the definition, even
if we can find a way to avoid making it circular.
A better strategy is to find a necessary and sufficient condition for
all the elements of a set    to be generated by to be generated by  when
applied only to sets of previously generated elements within when
applied only to sets of previously generated elements within  .
For example, taking .
For example, taking  to be the successor function, we can let to be the successor function, we can let
   rather than rather than   , and we will still have , and we will still have  
  as required. This gets rid of the circularity of the definition, since
we should have a condition to test whether a given set
as required. This gets rid of the circularity of the definition, since
we should have a condition to test whether a given set  is in is in  without knowing about any of the other elements of
without knowing about any of the other elements of  . .
The definition I ended up using accomplishes this using induction:  is defined as the class of sets
is defined as the class of sets  for which a sort of induction on
the elements of for which a sort of induction on
the elements of  holds. However, when creating a definition for
setrecs that did not rely on ordinal numbers, I tried at first to
write a definition using the well-founded relation predicate,
holds. However, when creating a definition for
setrecs that did not rely on ordinal numbers, I tried at first to
write a definition using the well-founded relation predicate, 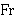 .
I thought that this would be simple to do once I found a suitable
definition using induction, just as the least- element principle is
equivalent to induction on the positive integers. If we let .
I thought that this would be simple to do once I found a suitable
definition using induction, just as the least- element principle is
equivalent to induction on the positive integers. If we let
   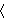    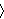          , then , then
  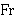        
     
                   . .
On 22-Jul-2020 I came up with the following definition (Version 1)
phrased in terms of induction:      
                           
In Aug-2020 I came up with an equivalent definition with the goal of
phrasing it in terms of the relation 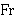 . It is the contrapositive
of the previous one with . It is the contrapositive
of the previous one with  replaced by its complement. replaced by its complement.
     
   
                 
    
These definitions didn't work because the induction didn't "get off
the
ground." If  does not contain the empty set, the condition does not contain the empty set, the condition
    
  fails, so fails, so    doesn't get included in
doesn't get included in
 even though it
should. This could be fixed by adding the base
case as a separate requirement, but the subtler problem would remain
that rather than a set of "acceptable" sets, what we really
need is a
collection even though it
should. This could be fixed by adding the base
case as a separate requirement, but the subtler problem would remain
that rather than a set of "acceptable" sets, what we really
need is a
collection  of
all individuals that have been generated so far. So
one approach is to replace every occurence of of
all individuals that have been generated so far. So
one approach is to replace every occurence of   with with   ,
making ,
making  a set of
individuals rather than a family of sets. That
solves this problem, but it complicates the foundedness version of the
definition, which looked cleaner in Version 1. a set of
individuals rather than a family of sets. That
solves this problem, but it complicates the foundedness version of the
definition, which looked cleaner in Version 1.
There was another problem with Version 1. If we let  be the power
set function, then the induction in the inductive version works for be the power
set function, then the induction in the inductive version works for
 being the class
of transitive sets, restricted to subsets of being the class
of transitive sets, restricted to subsets of
 . Therefore, . Therefore,
 must be transitive by
definition of must be transitive by
definition of  .
This doesn't affect the union of all such .
This doesn't affect the union of all such  , but it may or may not
be desirable. The problem is that , but it may or may not
be desirable. The problem is that  is only applied to transitive
sets, because of the strong requirement is only applied to transitive
sets, because of the strong requirement    , so the
definition
requires the additional constraint , so the
definition
requires the additional constraint        a ) C_ ( F a ) C_ ( F
   in order to work. This issue can also be avoided by replacing in order to work. This issue can also be avoided by replacing
  with with   . The induction version of the result is used in
the final definition. . The induction version of the result is used in
the final definition.
Version 2: (18-Aug-2020) Induction:      
                  
   
     Foundedness:
Foundedness:             
    
             
     
In the induction version, not only does  include all the elements
of include all the elements
of  , but it must
include the elements of , but it must
include the elements of      for for
    
  even if those elements of even if those elements of      are not in are not in
 . We shouldn't
care about any of the elements of . We shouldn't
care about any of the elements of  outside outside
 , but this detail
doesn't affect the correctness of the
definition. If we replaced , but this detail
doesn't affect the correctness of the
definition. If we replaced      in the definition by in the definition by
         , we would get
the same class for
setrecs , we would get
the same class for
setrecs   . Suppose we could find a . Suppose we could find a  for which the
condition fails for a given for which the
condition fails for a given  under the changed definition. Then
the antecedent would be true, but under the changed definition. Then
the antecedent would be true, but    would be
false. We could
then simply add all elements of would be
false. We could
then simply add all elements of      outside of outside of  for any for any
   , which we can do because all the classes
involved are sets.
This is not trivial and requires the axioms of union, power set, and
replacement. However, the expanded , which we can do because all the classes
involved are sets.
This is not trivial and requires the axioms of union, power set, and
replacement. However, the expanded  fails the condition under the
metamath definition. The other direction is easier. If a certain fails the condition under the
metamath definition. The other direction is easier. If a certain  fails the metamath definition, then all
fails the metamath definition, then all        for for
    
  , and in particular , and in particular       
    . .
The foundedness version is starting to look more like ax-reg 8497! We
want to take advantage of the preexisting relation 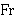 , which seems
closely related to our foundedness definition. Since we only care about
the elements of , which seems
closely related to our foundedness definition. Since we only care about
the elements of  which are subsets of
which are subsets of  ,
we can restrict ,
we can restrict  to
to  in the
foundedness definition. Furthermore, instead of
quantifying over in the
foundedness definition. Furthermore, instead of
quantifying over  , quantify over the elements , quantify over the elements  
 overlapping with
overlapping with  . Versions 3, 4, and 5 are all equivalent to
Version 2. . Versions 3, 4, and 5 are all equivalent to
Version 2.
Version 3 - Foundedness (5-Sep-2020):
            
  
         
                 
Now, if we replace      by by          , we do
not change the definition. We already know that , we do
not change the definition. We already know that    since
since
   and and  
 . All we need to show
in order to prove that
this change leads to an equivalent definition is to find . All we need to show
in order to prove that
this change leads to an equivalent definition is to find
To make our definition look exactly like df-fr 5073, we add another
variable 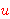 representing the nonexistent element of
representing the nonexistent element of  in in  . .
Version 4 - Foundedness (6-Sep-2020):
            
   
       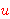 
   
   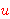
   
      
This is so close to df-fr 5073; the only change needed is to switch
  with with  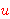 
 . Unfortunately, I
couldn't find any way to
switch the quantifiers without interfering with the definition. Maybe
there is a definition equivalent to this one that uses . Unfortunately, I
couldn't find any way to
switch the quantifiers without interfering with the definition. Maybe
there is a definition equivalent to this one that uses 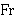 , but I
couldn't find one. Yet, we can still find a remarkable similarity
between Foundedness Version 2 and ax-reg 8497. Rather than a disjoint
element of , but I
couldn't find one. Yet, we can still find a remarkable similarity
between Foundedness Version 2 and ax-reg 8497. Rather than a disjoint
element of  ,
there's a disjoint coverer of an element of ,
there's a disjoint coverer of an element of  . .
Finally, here's a different dead end I followed:
To clean up our foundedness definition, we keep  as a family of
sets as a family of
sets  but allow but allow
 to be any subset of to be any subset of
  in the
induction. With this stronger induction, we can also allow for the
stronger requirement in the
induction. With this stronger induction, we can also allow for the
stronger requirement     rather than only rather than only    .
This
will help improve the foundedness version. .
This
will help improve the foundedness version.
Version 1.1 (28-Aug-2020) Induction:         
    
                 
    Foundedness:
Foundedness:                  
        
               
( Edit (Aug 31) - this isn't true! Nothing forces the subset of an
element of  to be
in to be
in  . Version 2 does not
have this issue. ) . Version 2 does not
have this issue. )
Similarly, we could allow  to be any subset of any element of to be any subset of any element of  rather than any subset of
rather than any subset of   . I
think this has the same problem. . I
think this has the same problem.
We want to take advantage of the preexisting relation 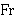 , which
seems closely related to our foundedness definition. Since we only care
about the elements of , which
seems closely related to our foundedness definition. Since we only care
about the elements of  which are subsets of which are subsets of  , we can restrict , we can restrict
 to to   in the foundedness definition: in the foundedness definition:
Version 1.2 (31-Aug-2020) Foundedness:
                
             
           
Now this looks more like df-fr 5073! The last step necessary to be able
to use 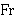 directly in our definition is to replace
directly in our definition is to replace      with its own setvar variable, corresponding to
with its own setvar variable, corresponding to  in df-fr 5073. in df-fr 5073.
This definition is incorrect, though, since there's nothing forcing the
subset of an element of  to be in to be in  . .
Version 1.3 (31-Aug-2020) Induction:             
                      
      Foundedness:
Foundedness:
                        
    
       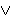           
 must contain the
supersets of each of its elements in the
foundedness version, and we can't make any restrictions on must contain the
supersets of each of its elements in the
foundedness version, and we can't make any restrictions on  or or
 , so this
doesn't work. , so this
doesn't work.
Let's try letting R be the covering relation
   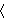    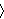  
       to solve the transitivity
issue (i.e. that if to solve the transitivity
issue (i.e. that if  is the power set relation, is the power set relation,  consists only
of transitive sets). The set consists only
of transitive sets). The set      corresponds to the variable corresponds to the variable
 in df-fr 5073. Thus, in our case, df-fr 5073 is equivalent to in df-fr 5073. Thus, in our case, df-fr 5073 is equivalent to
  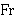        
     
                          .
Substituting our relation .
Substituting our relation  gives gives
  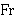        
      
                            
This doesn't work for non-injective  because we need all because we need all  to
be straddlers, but we don't necessarily need all-straddlers; loops
within z are fine for non-injective F. to
be straddlers, but we don't necessarily need all-straddlers; loops
within z are fine for non-injective F.
Consider the foundedness form of Version 1. We want to show
                 so we can replace one with
the other. Negate both sides: so we can replace one with
the other. Negate both sides:  
 
          
If  is
injective, then we should be able to pick a suitable R,
being careful about the above problem for some F (for example z =
transitivity) when changing the antecedent y e. z' to z =/= (/). If
we're clever, we can get rid of the injectivity requirement. The
forward direction of the above equivalence always holds, but the key is
that although the backwards direction doesn't hold in general, we can
always find some z' where it doesn't work for is
injective, then we should be able to pick a suitable R,
being careful about the above problem for some F (for example z =
transitivity) when changing the antecedent y e. z' to z =/= (/). If
we're clever, we can get rid of the injectivity requirement. The
forward direction of the above equivalence always holds, but the key is
that although the backwards direction doesn't hold in general, we can
always find some z' where it doesn't work for  itself. If there
exists a z' where the version with the w condition fails, then there
exists a z' where the version with the v condition also fails. However,
Version 1 is not a correct definition, so this doesn't work either.
(Contributed by Emmett Weisz, 18-Aug-2020.)
(New usage is discouraged.) itself. If there
exists a z' where the version with the w condition fails, then there
exists a z' where the version with the v condition also fails. However,
Version 1 is not a correct definition, so this doesn't work either.
(Contributed by Emmett Weisz, 18-Aug-2020.)
(New usage is discouraged.)
|
 setrecs setrecs                                      |
| |
| Theorem | setrecseq 42432 |
Equality theorem for set recursion. (Contributed by Emmett Weisz,
17-Feb-2021.)
|
   
  setrecs setrecs  
 setrecs setrecs    |
| |
| Theorem | nfsetrecs 42433 |
Bound-variable hypothesis builder for setrecs. (Contributed by
Emmett Weisz, 21-Oct-2021.)
|
        setrecs setrecs   |
| |
| Theorem | setrec1lem1 42434* |
Lemma for setrec1 42438. This is a utility theorem showing the
equivalence
of the statement    and its expanded form.
The proof uses
elabg 3351 and equivalence theorems. and its expanded form.
The proof uses
elabg 3351 and equivalence theorems.
Variable  is
the class of sets is
the class of sets  that
are recursively generated
by the function that
are recursively generated
by the function  . In other words, . In other words,    iff by starting with
the empty set and repeatedly applying iff by starting with
the empty set and repeatedly applying  to subsets to subsets  of our set,
we will eventually generate all the elements of of our set,
we will eventually generate all the elements of  . In this
theorem, . In this
theorem,  is
any element of is
any element of  , and , and
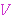 is any class.
(Contributed by Emmett Weisz, 16-Oct-2020.)
(New usage is discouraged.) is any class.
(Contributed by Emmett Weisz, 16-Oct-2020.)
(New usage is discouraged.)
|
            
    
             
           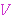                               
    
      |
| |
| Theorem | setrec1lem2 42435* |
Lemma for setrec1 42438. If a family of sets are all recursively
generated
by  , so is
their union. In this theorem, , so is
their union. In this theorem,  is a family of
sets which are all elements of is a family of
sets which are all elements of  , and , and 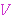 is any class. Use
dfss3 3592, equivalence and equality theorems, and
unissb at the end.
Sandwich with applications of setrec1lem1. (Contributed by Emmett
Weisz, 24-Jan-2021.) (New usage is discouraged.) is any class. Use
dfss3 3592, equivalence and equality theorems, and
unissb at the end.
Sandwich with applications of setrec1lem1. (Contributed by Emmett
Weisz, 24-Jan-2021.) (New usage is discouraged.)
|
            
    
             
           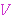                     |
| |
| Theorem | setrec1lem3 42436* |
Lemma for setrec1 42438. If each element  of of  is covered by a
set is covered by a
set  recursively
generated by recursively
generated by  , then
there is a single such
set covering all of , then
there is a single such
set covering all of  . The set is constructed explicitly using
setrec1lem2 42435. It turns out that . The set is constructed explicitly using
setrec1lem2 42435. It turns out that    also works, i.e., given the
hypotheses it is possible to prove that
also works, i.e., given the
hypotheses it is possible to prove that    . I don't
know if
proving this fact directly using setrec1lem1 42434 would be any easier than
the current proof using setrec1lem2 42435, and it would only slightly
simplify the proof of setrec1 42438. Other than the use of bnd2d 42428, this
is a purely technical theorem for rearranging notation from that of
setrec1lem2 42435 to that of setrec1 42438. (Contributed by Emmett Weisz,
20-Jan-2021.) (New usage is discouraged.) . I don't
know if
proving this fact directly using setrec1lem1 42434 would be any easier than
the current proof using setrec1lem2 42435, and it would only slightly
simplify the proof of setrec1 42438. Other than the use of bnd2d 42428, this
is a purely technical theorem for rearranging notation from that of
setrec1lem2 42435 to that of setrec1 42438. (Contributed by Emmett Weisz,
20-Jan-2021.) (New usage is discouraged.)
|
            
    
             
                                                   |
| |
| Theorem | setrec1lem4 42437* |
Lemma for setrec1 42438. If  is recursively generated by is recursively generated by  , then
so is , then
so is  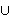      . .
In the proof of setrec1 42438, the following is substituted for this
theorem's  : :     
    
       
    
    
                 Therefore, we cannot declare
Therefore, we cannot declare  to be a distinct variable from to be a distinct variable from
 , since
we need it to appear as a bound variable in , since
we need it to appear as a bound variable in  .
This theorem can be proven without the hypothesis .
This theorem can be proven without the hypothesis 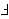   , but the
proof would be harder to read because theorems in deduction form would
be interrupted by theorems like eximi 1762, making the antecedent of each
line something more complicated than , but the
proof would be harder to read because theorems in deduction form would
be interrupted by theorems like eximi 1762, making the antecedent of each
line something more complicated than  . The proof of
setrec1lem2 42435 could similarly be made easier to read by
adding the
hypothesis . The proof of
setrec1lem2 42435 could similarly be made easier to read by
adding the
hypothesis 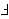   , but I had already
finished the proof and
decided to leave it as is. (Contributed by Emmett Weisz, 26-Nov-2020.)
(New usage is discouraged.) , but I had already
finished the proof and
decided to leave it as is. (Contributed by Emmett Weisz, 26-Nov-2020.)
(New usage is discouraged.)
|
 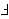                                                                          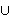          |
| |
| Theorem | setrec1 42438 |
This is the first of two fundamental theorems about set recursion from
which all other facts will be derived. It states that the class
setrecs   is closed under is closed under  . This effectively sets the
actual value of setrecs . This effectively sets the
actual value of setrecs   as a lower bound for
setrecs as a lower bound for
setrecs   , as it implies that any set generated by
successive
applications of , as it implies that any set generated by
successive
applications of  is a member of is a member of  . This theorem "gets off the
ground" because we can start by letting . This theorem "gets off the
ground" because we can start by letting    , and the hypotheses
of the theorem will hold trivially. , and the hypotheses
of the theorem will hold trivially.
Variable  represents an abbreviation of setrecs
represents an abbreviation of setrecs   or
another name of setrecs or
another name of setrecs   (for an example of the
latter, see
theorem setrecon). (for an example of the
latter, see
theorem setrecon).
Proof summary: Assume that  
 , meaning that all
elements of , meaning that all
elements of
 are in some
set recursively generated by are in some
set recursively generated by  . Then by
setrec1lem3 42436, . Then by
setrec1lem3 42436,  is a subset of some set recursively generated by is a subset of some set recursively generated by
 . (It turns
out that . (It turns
out that  itself is
recursively generated by itself is
recursively generated by
 , but we don't
need this fact. See the comment to
setrec1lem3 42436.) Therefore, by setrec1lem4 42437, , but we don't
need this fact. See the comment to
setrec1lem3 42436.) Therefore, by setrec1lem4 42437,      is a
subset of some set recursively generated by is a
subset of some set recursively generated by  . Thus, by ssuni 4459,
it is a subset of the union of all sets recursively generated by . Thus, by ssuni 4459,
it is a subset of the union of all sets recursively generated by  . .
See df-setrecs 42431 for a detailed description of how the
setrecs
definition works.
(Contributed by Emmett Weisz, 9-Oct-2020.)
|
   setrecs setrecs                                  |
| |
| Theorem | setrec2fun 42439* |
This is the second of two fundamental theorems about set recursion from
which all other facts will be derived. It states that the class
setrecs   is a subclass of all classes is a subclass of all classes  that are closed
under that are closed
under  . Taken
together, theorems setrec1 42438 and setrec2v 42443 say
that setrecs . Taken
together, theorems setrec1 42438 and setrec2v 42443 say
that setrecs   is the minimal class closed under is the minimal class closed under  . .
We express this by saying that if  respects the respects the  relation and relation and
 is closed
under is closed
under  , then , then    . By substituting
strategically constructed classes for . By substituting
strategically constructed classes for  , we can easily prove many
useful properties. Although this theorem cannot show equality between , we can easily prove many
useful properties. Although this theorem cannot show equality between
 and and  , if we intend to prove
equality between , if we intend to prove
equality between  and
some
particular class (such as and
some
particular class (such as  ), we first apply this theorem, then
the relevant induction theorem (such as tfi 7053)
to the other class. ), we first apply this theorem, then
the relevant induction theorem (such as tfi 7053)
to the other class.
(Contributed by Emmett Weisz, 15-Feb-2021.)
(New usage is discouraged.)
|
        setrecs
setrecs     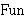                   
            |
| |
| Theorem | setrec2lem1 42440* |
Lemma for setrec2 42442. The functional part of  has the same values
as has the same values
as  .
(Contributed by Emmett Weisz, 4-Mar-2021.)
(New usage is discouraged.) .
(Contributed by Emmett Weisz, 4-Mar-2021.)
(New usage is discouraged.)
|
    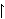    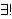         
      |
| |
| Theorem | setrec2lem2 42441* |
Lemma for setrec2 42442. The functional part of  is a function.
(Contributed by Emmett Weisz, 6-Mar-2021.)
(New usage is discouraged.) is a function.
(Contributed by Emmett Weisz, 6-Mar-2021.)
(New usage is discouraged.)
|
 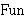  
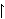    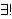       |
| |
| Theorem | setrec2 42442* |
This is the second of two fundamental theorems about set recursion from
which all other facts will be derived. It states that the class
setrecs   is a subclass of all classes is a subclass of all classes  that are closed
under that are closed
under  . Taken
together, theorems setrec1 42438 and setrec2v 42443
uniquely determine setrecs . Taken
together, theorems setrec1 42438 and setrec2v 42443
uniquely determine setrecs   to be the minimal class
closed
under to be the minimal class
closed
under  . .
We express this by saying that if  respects the respects the  relation and relation and
 is closed
under is closed
under  , then , then    . By substituting
strategically constructed classes for . By substituting
strategically constructed classes for  , we can easily prove many
useful properties. Although this theorem cannot show equality between , we can easily prove many
useful properties. Although this theorem cannot show equality between
 and and  , if we intend to prove
equality between , if we intend to prove
equality between  and
some
particular class (such as and
some
particular class (such as  ), we first apply this theorem, then
the relevant induction theorem (such as tfi 7053)
to the other class. ), we first apply this theorem, then
the relevant induction theorem (such as tfi 7053)
to the other class.
(Contributed by Emmett Weisz, 2-Sep-2021.)
|
        setrecs
setrecs       
    
               
    |
| |
| Theorem | setrec2v 42443* |
Version of setrec2 42442 with a dv condition instead of a
non-freeness
hypothesis. (Contributed by Emmett Weisz, 6-Mar-2021.)
|
   setrecs setrecs                                 |
| |
| 20.36.2.2 Examples and properties of set
recursion
|
| |
| Theorem | elsetrecslem 42444* |
Lemma for elsetrecs 42445. Any element of setrecs   is
generated
by some subset of setrecs is
generated
by some subset of setrecs   . This is much weaker than
setrec2v 42443. To see why this lemma also requires setrec1 42438, consider
what would happen if we replaced . This is much weaker than
setrec2v 42443. To see why this lemma also requires setrec1 42438, consider
what would happen if we replaced  with with    . The
antecedent would still hold, but the consequent would fail in general.
Consider dispensing with the deduction form. (Contributed by Emmett
Weisz, 11-Jul-2021.) (New usage is discouraged.) . The
antecedent would still hold, but the consequent would fail in general.
Consider dispensing with the deduction form. (Contributed by Emmett
Weisz, 11-Jul-2021.) (New usage is discouraged.)
|
   setrecs setrecs                          |
| |
| Theorem | elsetrecs 42445* |
A set  is an element
of setrecs is an element
of setrecs   iff iff  is generated
by some subset of setrecs is generated
by some subset of setrecs   . The proof requires both
setrec1 42438 and setrec2 42442, but this theorem is not strong enough to
uniquely determine setrecs . The proof requires both
setrec1 42438 and setrec2 42442, but this theorem is not strong enough to
uniquely determine setrecs   . If . If  respects the subset
relation, the theorem still holds if both occurrences of respects the subset
relation, the theorem still holds if both occurrences of  are
replaced by are
replaced by  for a stronger version of the theorem.
(Contributed by Emmett Weisz, 12-Jul-2021.) for a stronger version of the theorem.
(Contributed by Emmett Weisz, 12-Jul-2021.)
|
   setrecs setrecs                          |
| |
| Theorem | vsetrec 42446 |
Construct  using
set recursion. The proof indirectly uses
trcl 8604, which relies on using
set recursion. The proof indirectly uses
trcl 8604, which relies on 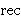 , but theoretically , but theoretically  in trcl 8604
could be constructed using setrecs instead. The proof of this
theorem uses the dummy variable in trcl 8604
could be constructed using setrecs instead. The proof of this
theorem uses the dummy variable  rather than rather than  to avoid a
distinct variable requirement between to avoid a
distinct variable requirement between  and and  . (Contributed by
Emmett Weisz, 23-Jun-2021.) . (Contributed by
Emmett Weisz, 23-Jun-2021.)
|
             setrecs setrecs     |
| |
| Theorem | 0setrec 42447 |
If a function sends the empty set to itself, the function will not
recursively generate any sets, regardless of its other values.
(Contributed by Emmett Weisz, 23-Jun-2021.)
|
                 setrecs setrecs  
   |
| |
| Theorem | onsetreclem1 42448* |
Lemma for onsetrec 42451. (Contributed by Emmett Weisz,
22-Jun-2021.)
(New usage is discouraged.)
|
            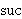           
     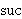    |
| |
| Theorem | onsetreclem2 42449* |
Lemma for onsetrec 42451. (Contributed by Emmett Weisz,
22-Jun-2021.)
(New usage is discouraged.)
|
            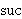                
   |
| |
| Theorem | onsetreclem3 42450* |
Lemma for onsetrec 42451. (Contributed by Emmett Weisz,
22-Jun-2021.)
(New usage is discouraged.)
|
            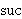                    |
| |
| Theorem | onsetrec 42451 |
Construct  using set
recursion. When using set
recursion. When    , the function , the function
 constructs the
least ordinal greater than any of the elements of constructs the
least ordinal greater than any of the elements of
 , which is , which is   for a limit ordinal and for a limit ordinal and 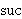   for a
successor ordinal. for a
successor ordinal.
For example,       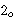  
      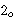   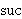     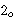     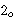  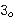  which
contains which
contains 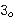 ,
and ,
and
    
     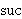         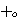   , which
contains , which
contains  .
If we start with the empty set and keep applying .
If we start with the empty set and keep applying
 transfinitely
many times, all ordinal numbers will be generated. transfinitely
many times, all ordinal numbers will be generated.
Any function  fulfilling lemmas onsetreclem2 42449 and onsetreclem3 42450
will recursively generate
fulfilling lemmas onsetreclem2 42449 and onsetreclem3 42450
will recursively generate  ; for example, ; for example,
       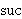 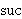     also works. Whether this
function or the function in the theorem is used, taking this theorem as
a definition of also works. Whether this
function or the function in the theorem is used, taking this theorem as
a definition of  is unsatisfying because it relies on the
different properties of limit and successor ordinals. A different
approach could be to let is unsatisfying because it relies on the
different properties of limit and successor ordinals. A different
approach could be to let              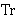    ,
based on dfon2 31697. ,
based on dfon2 31697.
The proof of this theorem uses the dummy variable  rather than rather than
 to avoid a
distinct variable condition between to avoid a
distinct variable condition between  and and  .
(Contributed by Emmett Weisz, 22-Jun-2021.) .
(Contributed by Emmett Weisz, 22-Jun-2021.)
|
            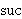       setrecs setrecs     |
| |
| 20.36.3 Construction of Games and Surreal
Numbers
Model organization after organization of reals - see TOC
|
| |
| Syntax | cpg 42452 |
Extend class notation to include the class of partizan game forms.
|
 Pg Pg |
| |
| Definition | df-pg 42453 |
Define the class of partizan games. More precisely, this is the class of
partizan game forms, many of which represent equal partisan games. In
metamath, equality between partizan games is represented by a different
equivalence relation than class equality. (Contributed by Emmett Weisz,
22-Aug-2021.)
|
 Pg Pg  setrecs setrecs         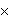      |
| |
| Theorem | elpglem1 42454* |
Lemma for elpg 42457. (Contributed by Emmett Weisz,
28-Aug-2021.)
|
       Pg Pg        
        
   
        Pg Pg        Pg Pg  |
| |
| Theorem | elpglem2 42455* |
Lemma for elpg 42457. (Contributed by Emmett Weisz,
28-Aug-2021.)
|
         Pg Pg 
      Pg Pg       Pg Pg        
        
     |
| |
| Theorem | elpglem3 42456* |
Lemma for elpg 42457. (Contributed by Emmett Weisz,
28-Aug-2021.)
|
       Pg Pg             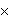               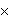         Pg Pg                 
      |
| |
| Theorem | elpg 42457 |
Membership in the class of partizan games. In ONAG this is stated as
"If  and and
 are any two sets of
games, then there is a game are any two sets of
games, then there is a game
     .
All games are constructed in this way." The first
sentence corresponds to the backward direction of our theorem, and the
second to the forward direction. (Contributed by Emmett Weisz,
27-Aug-2021.) .
All games are constructed in this way." The first
sentence corresponds to the backward direction of our theorem, and the
second to the forward direction. (Contributed by Emmett Weisz,
27-Aug-2021.)
|
    Pg
Pg       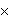          Pg Pg 
      Pg Pg  |
| |
| 20.37 Mathbox for David A.
Wheeler
This is the mathbox of David A. Wheeler, dwheeler at dwheeler dot com.
Among other things, I have added a number of formal definitions for
widely-used functions, e.g., those defined in
ISO 80000-2:2009(E)
Quantities and units - Part 2: Mathematical signs and
symbols used in the natural sciences and technology
and the
NIST Digital Library of Mathematical Functions http://dlmf.nist.gov/.
|
| |
| 20.37.1 Natural deduction
|
| |
| Theorem | 19.8ad 42458 |
If a wff is true, it is true for at least one instance. Deductive form
of 19.8a 2052. (Contributed by DAW, 13-Feb-2017.)
|
               |
| |
| Theorem | sbidd 42459 |
An identity theorem for substitution. See sbid 2114.
See Remark 9.1 in
[Megill] p. 447 (p. 15 of the preprint).
(Contributed by DAW,
18-Feb-2017.)
|
    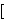    ![] ]](rbrack.gif)          |
| |
| Theorem | sbidd-misc 42460 |
An identity theorem for substitution. See sbid 2114.
See Remark 9.1 in
[Megill] p. 447 (p. 15 of the preprint).
(Contributed by DAW,
18-Feb-2017.)
|
   
 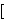    ![] ]](rbrack.gif)          |
| |
| 20.37.2 Greater than, greater than or equal
to.
As a stylistic issue, set.mm prefers 'less than' instead of
'greater than' to reduce the number of conversion steps.
Here we formally define the widely-used relations
'greater than' and 'greater than or equal to', so that we
have formal definitions of them, as well as a few related theorems.
|
| |
| Syntax | cge-real 42461 |
Extend wff notation to include the 'greater than or equal to' relation,
see df-gte 42463.
|
 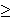 |
| |
| Syntax | cgt 42462 |
Extend wff notation to include the 'greater than' relation, see
df-gt 42464.
|
 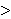 |
| |
| Definition | df-gte 42463 |
Define the 'greater than or equal' predicate over the reals. Defined in
ISO 80000-2:2009(E) operation 2-7.10. It is used as a primitive in the
"NIST Digital Library of Mathematical Functions" , front
introduction,
"Common Notations and Definitions" section at
http://dlmf.nist.gov/front/introduction#Sx4.
This relation is merely
the converse of the 'less than or equal to' relation defined by df-le 10080.
We do not write this as   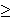    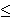   , and similarly we do
not write ` > ` as , and similarly we do
not write ` > ` as   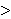       , because these are not
definitional axioms as understood by mmj2 (those definitions will be
flagged as being "potentially non-conservative"). We could
write them
this way: , because these are not
definitional axioms as understood by mmj2 (those definitions will be
flagged as being "potentially non-conservative"). We could
write them
this way:
 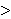   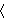    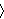 
    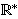    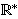        and and
 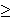   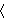    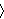 
    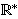    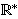    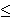    but
these are very complicated. This definition of but
these are very complicated. This definition of 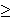 , and the similar
one for , and the similar
one for 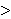 (df-gt 42464), are a bit strange when you see them for
the
first time, but these definitions are much simpler for us to process and
are clearly conservative definitions. (My thanks to Mario Carneiro for
pointing out this simpler approach.) See gte-lte 42465 for a more
conventional expression of the relationship between (df-gt 42464), are a bit strange when you see them for
the
first time, but these definitions are much simpler for us to process and
are clearly conservative definitions. (My thanks to Mario Carneiro for
pointing out this simpler approach.) See gte-lte 42465 for a more
conventional expression of the relationship between  and and 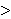 . As
a stylistic issue, set.mm prefers 'less than' instead of 'greater than' to
reduce the number of conversion steps. Thus, we discourage its use, but
include its definition so that there is a formal definition of this
symbol. . As
a stylistic issue, set.mm prefers 'less than' instead of 'greater than' to
reduce the number of conversion steps. Thus, we discourage its use, but
include its definition so that there is a formal definition of this
symbol.
(Contributed by David A. Wheeler, 10-May-2015.)
(New usage is discouraged.)
|
 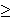   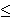 |
| |
| Definition | df-gt 42464 |
The 'greater than' relation is merely the converse of the 'less than or
equal to' relation defined by df-lt 9949. Defined in ISO 80000-2:2009(E)
operation 2-7.12. See df-gte 42463 for a discussion on why this approach is
used for the definition. See gt-lt 42466 and gt-lth 42468 for more conventional
expression of the relationship between  and and 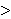 . .
As a stylistic issue, set.mm prefers 'less than or equal' instead of
'greater than or equal' to reduce the number of conversion steps. Thus,
we discourage its use, but include its definition so that there is
a
formal definition of this symbol.
(Contributed by David A. Wheeler, 19-Apr-2015.)
(New usage is discouraged.)
|
 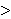    |
| |
| Theorem | gte-lte 42465 |
Simple relationship between 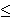 and and 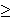 . (Contributed by David A.
Wheeler, 10-May-2015.) (New usage is discouraged.) . (Contributed by David A.
Wheeler, 10-May-2015.) (New usage is discouraged.)
|
              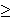    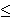    |
| |
| Theorem | gt-lt 42466 |
Simple relationship between  and and 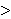 . (Contributed by David A.
Wheeler, 19-Apr-2015.) (New usage is discouraged.) . (Contributed by David A.
Wheeler, 19-Apr-2015.) (New usage is discouraged.)
|
              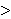        |
| |
| Theorem | gte-lteh 42467 |
Relationship between 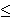 and and 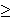 using hypotheses. (Contributed
by David A. Wheeler, 10-May-2015.) (New usage is discouraged.) using hypotheses. (Contributed
by David A. Wheeler, 10-May-2015.) (New usage is discouraged.)
|
             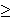   
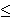   |
| |
| Theorem | gt-lth 42468 |
Relationship between  and and 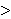 using hypotheses. (Contributed by
David A. Wheeler, 19-Apr-2015.) (New usage is discouraged.) using hypotheses. (Contributed by
David A. Wheeler, 19-Apr-2015.) (New usage is discouraged.)
|
             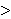   
   |
| |
| Theorem | ex-gt 42469 |
Simple example of 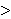 , in this case, 0 is not greater than 0. This is
useful as an example, and helps us gain confidence that we've correctly
defined the symbol. (Contributed by David A. Wheeler, 1-Jan-2017.)
(New usage is discouraged.) , in this case, 0 is not greater than 0. This is
useful as an example, and helps us gain confidence that we've correctly
defined the symbol. (Contributed by David A. Wheeler, 1-Jan-2017.)
(New usage is discouraged.)
|
   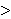  |
| |
| Theorem | ex-gte 42470 |
Simple example of 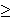 , in this case, 0 is greater than or equal to 0.
This is useful as an example, and helps us gain confidence that we've
correctly defined the symbol. (Contributed by David A. Wheeler,
1-Jan-2017.) (New usage is discouraged.) , in this case, 0 is greater than or equal to 0.
This is useful as an example, and helps us gain confidence that we've
correctly defined the symbol. (Contributed by David A. Wheeler,
1-Jan-2017.) (New usage is discouraged.)
|
  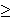  |
| |
| 20.37.3 Hyperbolic trigonometric
functions
It is a convention of set.mm to not use sinh and so on directly,
and instead of use expansions such as  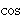        .
However, I believe it's important to give formal definitions for
these conventional functions as they are typically used,
so here they are. A few related identities are also proved. .
However, I believe it's important to give formal definitions for
these conventional functions as they are typically used,
so here they are. A few related identities are also proved.
|
| |
| Syntax | csinh 42471 |
Extend class notation to include the hyperbolic sine function, see
df-sinh 42474.
|
 sinh sinh |
| |
| Syntax | ccosh 42472 |
Extend class notation to include the hyperbolic cosine function. see
df-cosh 42475.
|
 cosh cosh |
| |
| Syntax | ctanh 42473 |
Extend class notation to include the hyperbolic tangent function, see
df-tanh 42476.
|
 tanh tanh |
| |
| Definition | df-sinh 42474 |
Define the hyperbolic sine function (sinh). We define it this way for
cmpt 4729, which requires the form        . See
sinhval-named 42477 for a simple way to evaluate it. We define
this function
by dividing by . See
sinhval-named 42477 for a simple way to evaluate it. We define
this function
by dividing by  ,
which uses fewer operations than many conventional
definitions (and thus is more convenient to use in metamath). See
sinh-conventional 42480 for a justification that our definition is
the same as
the conventional definition of sinh used in other sources. (Contributed
by David A. Wheeler, 20-Apr-2015.) ,
which uses fewer operations than many conventional
definitions (and thus is more convenient to use in metamath). See
sinh-conventional 42480 for a justification that our definition is
the same as
the conventional definition of sinh used in other sources. (Contributed
by David A. Wheeler, 20-Apr-2015.)
|
 sinh sinh         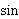            |
| |
| Definition | df-cosh 42475 |
Define the hyperbolic cosine function (cosh). We define it this way for
cmpt 4729, which requires the form        . (Contributed by
David A. Wheeler, 10-May-2015.) . (Contributed by
David A. Wheeler, 10-May-2015.)
|
 cosh cosh        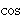         |
| |
| Definition | df-tanh 42476 |
Define the hyperbolic tangent function (tanh). We define it this way for
cmpt 4729, which requires the form        . (Contributed by
David A. Wheeler, 10-May-2015.) . (Contributed by
David A. Wheeler, 10-May-2015.)
|
 tanh tanh       cosh cosh                   
    |
| |
| Theorem | sinhval-named 42477 |
Value of the named sinh function. Here we show the simple conversion to
the conventional form used in set.mm, using the definition given by
df-sinh 42474. See sinhval 14884 for a theorem to convert this further. See
sinh-conventional 42480 for a justification that our
definition is the same
as the conventional definition of sinh used in other sources.
(Contributed by David A. Wheeler, 20-Apr-2015.)
|
   
   sinh sinh      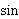            |
| |
| Theorem | coshval-named 42478 |
Value of the named cosh function. Here we show the simple conversion to
the conventional form used in set.mm, using the definition given by
df-cosh 42475. See coshval 14885 for a theorem to convert this further.
(Contributed by David A. Wheeler, 10-May-2015.)
|
   
   cosh cosh     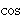         |
| |
| Theorem | tanhval-named 42479 |
Value of the named tanh function. Here we show the simple conversion to
the conventional form used in set.mm, using the definition given by
df-tanh 42476. (Contributed by David A. Wheeler,
10-May-2015.)
|
   
  cosh cosh           tanh tanh                  |
| |
| Theorem | sinh-conventional 42480 |
Conventional definition of sinh. Here we show that the sinh definition
we're using has the same meaning as the conventional definition used in
some other sources. We choose a slightly different definition of sinh
because it has fewer operations, and thus is more convenient to manipulate
using metamath. (Contributed by David A. Wheeler, 10-May-2015.)
|
   
   sinh sinh         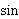          |
| |
| Theorem | sinhpcosh 42481 |
Prove that  sinh sinh     cosh cosh     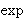    using the
conventional hyperbolic trigonometric functions. (Contributed by David A.
Wheeler, 27-May-2015.) using the
conventional hyperbolic trigonometric functions. (Contributed by David A.
Wheeler, 27-May-2015.)
|
   
    sinh sinh     cosh cosh      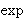     |
| |
| 20.37.4 Reciprocal trigonometric functions
(sec, csc, cot)
Define the traditional reciprocal trigonometric functions
secant (sec), cosecant (csc), and cotangent (cos), along with
various identities involving them.
|
| |
| Syntax | csec 42482 |
Extend class notation to include the secant function, see df-sec 42485.
|
 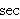 |
| |
| Syntax | ccsc 42483 |
Extend class notation to include the cosecant function, see df-csc 42486.
|
  |
| |
| Syntax | ccot 42484 |
Extend class notation to include the cotangent function, see df-cot 42487.
|
 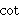 |
| |
| Definition | df-sec 42485* |
Define the secant function. We define it this way for cmpt 4729,
which
requires the form        . The sec
function is defined in
ISO 80000-2:2009(E) operation 2-13.6 and "NIST Digital Library of
Mathematical Functions" section on "Trigonometric
Functions"
http://dlmf.nist.gov/4.14
(Contributed by David A. Wheeler,
14-Mar-2014.) . The sec
function is defined in
ISO 80000-2:2009(E) operation 2-13.6 and "NIST Digital Library of
Mathematical Functions" section on "Trigonometric
Functions"
http://dlmf.nist.gov/4.14
(Contributed by David A. Wheeler,
14-Mar-2014.)
|
 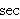           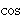            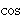      |
| |
| Definition | df-csc 42486* |
Define the cosecant function. We define it this way for cmpt 4729,
which
requires the form        . The csc
function is defined in
ISO 80000-2:2009(E) operation 2-13.7 and "NIST Digital Library of
Mathematical Functions" section on "Trigonometric
Functions"
http://dlmf.nist.gov/4.14
(Contributed by David A. Wheeler,
14-Mar-2014.) . The csc
function is defined in
ISO 80000-2:2009(E) operation 2-13.7 and "NIST Digital Library of
Mathematical Functions" section on "Trigonometric
Functions"
http://dlmf.nist.gov/4.14
(Contributed by David A. Wheeler,
14-Mar-2014.)
|
            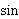            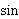      |
| |
| Definition | df-cot 42487* |
Define the cotangent function. We define it this way for cmpt 4729,
which
requires the form        . The cot
function is defined in
ISO 80000-2:2009(E) operation 2-13.5 and "NIST Digital Library of
Mathematical Functions" section on "Trigonometric
Functions"
http://dlmf.nist.gov/4.14
(Contributed by David A. Wheeler,
14-Mar-2014.) . The cot
function is defined in
ISO 80000-2:2009(E) operation 2-13.5 and "NIST Digital Library of
Mathematical Functions" section on "Trigonometric
Functions"
http://dlmf.nist.gov/4.14
(Contributed by David A. Wheeler,
14-Mar-2014.)
|
 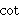           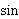          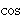      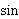      |
| |
| Theorem | secval 42488 |
Value of the secant function. (Contributed by David A. Wheeler,
14-Mar-2014.)
|
        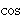         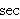         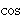      |
| |
| Theorem | cscval 42489 |
Value of the cosecant function. (Contributed by David A. Wheeler,
14-Mar-2014.)
|
        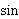                  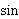      |
| |
| Theorem | cotval 42490 |
Value of the cotangent function. (Contributed by David A. Wheeler,
14-Mar-2014.)
|
        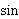         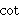       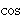      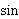      |
| |
| Theorem | seccl 42491 |
The closure of the secant function with a complex argument. (Contributed
by David A. Wheeler, 14-Mar-2014.)
|
        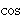         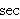       |
| |
| Theorem | csccl 42492 |
The closure of the cosecant function with a complex argument.
(Contributed by David A. Wheeler, 14-Mar-2014.)
|
        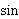                |
| |
| Theorem | cotcl 42493 |
The closure of the cotangent function with a complex argument.
(Contributed by David A. Wheeler, 15-Mar-2014.)
|
        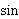         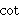       |
| |
| Theorem | reseccl 42494 |
The closure of the secant function with a real argument. (Contributed by
David A. Wheeler, 15-Mar-2014.)
|
     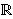   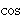         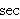     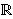  |
| |
| Theorem | recsccl 42495 |
The closure of the cosecant function with a real argument. (Contributed
by David A. Wheeler, 15-Mar-2014.)
|
     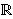   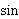              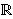  |
| |
| Theorem | recotcl 42496 |
The closure of the cotangent function with a real argument. (Contributed
by David A. Wheeler, 15-Mar-2014.)
|
     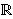   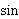         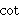     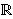  |
| |
| Theorem | recsec 42497 |
The reciprocal of secant is cosine. (Contributed by David A. Wheeler,
14-Mar-2014.)
|
        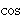         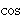         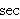      |
| |
| Theorem | reccsc 42498 |
The reciprocal of cosecant is sine. (Contributed by David A. Wheeler,
14-Mar-2014.)
|
        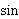         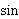               |
| |
| Theorem | reccot 42499 |
The reciprocal of cotangent is tangent. (Contributed by David A. Wheeler,
21-Mar-2014.)
|
        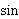        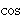                  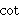      |
| |
| Theorem | rectan 42500 |
The reciprocal of tangent is cotangent. (Contributed by David A. Wheeler,
21-Mar-2014.)
|
        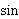        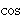         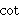               |