| Step | Hyp | Ref
| Expression |
|---|
| 1 | | elex 3212 |
. 2
          |
| 2 | | fveq2 6191 |
. . . . 5
       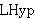      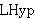     |
| 3 | | hdmapval.h |
. . . . 5
    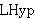    |
| 4 | 2, 3 | syl6eqr 2674 |
. . . 4
       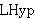       |
| 5 | | fveq2 6191 |
. . . . . . . 8
                  |
| 6 | 5 | reseq2d 5396 |
. . . . . . 7
                  
       |
| 7 | | fveq2 6191 |
. . . . . . . . 9
                  |
| 8 | 7 | fveq1d 6193 |
. . . . . . . 8
                          |
| 9 | 8 | reseq2d 5396 |
. . . . . . 7
                      
           |
| 10 | 6, 9 | opeq12d 4410 |
. . . . . 6
                   
                                      |
| 11 | | fveq2 6191 |
. . . . . . . 8
                  |
| 12 | 11 | fveq1d 6193 |
. . . . . . 7
                          |
| 13 | | fveq2 6191 |
. . . . . . . . . 10
       HDMap1 HDMap1     HDMap1 HDMap1    |
| 14 | 13 | fveq1d 6193 |
. . . . . . . . 9
        HDMap1 HDMap1         HDMap1 HDMap1       |
| 15 | | fveq2 6191 |
. . . . . . . . . . . . . 14
       LCDual LCDual     LCDual LCDual    |
| 16 | 15 | fveq1d 6193 |
. . . . . . . . . . . . 13
        LCDual LCDual         LCDual LCDual       |
| 17 | 16 | fveq2d 6195 |
. . . . . . . . . . . 12
           LCDual LCDual             LCDual LCDual        |
| 18 | | fveq2 6191 |
. . . . . . . . . . . . . . . . . . . . 21
       HVMap HVMap     HVMap HVMap    |
| 19 | 18 | fveq1d 6193 |
. . . . . . . . . . . . . . . . . . . 20
        HVMap HVMap         HVMap HVMap       |
| 20 | 19 | fveq1d 6193 |
. . . . . . . . . . . . . . . . . . 19
         HVMap HVMap             HVMap HVMap          |
| 21 | 20 | oteq2d 4415 |
. . . . . . . . . . . . . . . . . 18
            HVMap HVMap                   HVMap HVMap             |
| 22 | 21 | fveq2d 6195 |
. . . . . . . . . . . . . . . . 17
               HVMap HVMap                       HVMap HVMap              |
| 23 | 22 | oteq2d 4415 |
. . . . . . . . . . . . . . . 16
                  HVMap HVMap                             HVMap HVMap                 |
| 24 | 23 | fveq2d 6195 |
. . . . . . . . . . . . . . 15
                     HVMap HVMap                                 HVMap HVMap                  |
| 25 | 24 | eqeq2d 2632 |
. . . . . . . . . . . . . 14
                        HVMap HVMap                                   HVMap HVMap                   |
| 26 | 25 | imbi2d 330 |
. . . . . . . . . . . . 13
                                                      HVMap HVMap                                                                  HVMap HVMap                    |
| 27 | 26 | ralbidv 2986 |
. . . . . . . . . . . 12
        
                                                 HVMap HVMap                                                                      HVMap HVMap                    |
| 28 | 17, 27 | riotaeqbidv 6614 |
. . . . . . . . . . 11
               LCDual LCDual                                                          HVMap HVMap                      
      LCDual LCDual          
   
                                           HVMap HVMap                    |
| 29 | 28 | mpteq2dv 4745 |
. . . . . . . . . 10
             
      LCDual LCDual          
   
                                           HVMap HVMap                                   LCDual LCDual         
   
                          
                 HVMap HVMap                     |
| 30 | 29 | eleq2d 2687 |
. . . . . . . . 9
                       LCDual LCDual         
   
                          
                 HVMap HVMap                                     LCDual LCDual         
   
                          
                 HVMap HVMap                      |
| 31 | 14, 30 | sbceqbid 3442 |
. . . . . . . 8
          HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                        HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                      |
| 32 | 31 | sbcbidv 3490 |
. . . . . . 7
               ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                             ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                      |
| 33 | 12, 32 | sbceqbid 3442 |
. . . . . 6
                   ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)  
   
          LCDual LCDual         
   
                          
                 HVMap HVMap                                 ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)  
   
          LCDual LCDual         
   
                          
                 HVMap HVMap                      |
| 34 | 10, 33 | sbceqbid 3442 |
. . . . 5
                                   ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                                                 ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                      |
| 35 | 34 | abbidv 2741 |
. . . 4
                       
             ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                                       
             ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                      |
| 36 | 4, 35 | mpteq12dv 4733 |
. . 3
          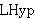                      
             ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                                   
                       ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                       |
| 37 | | df-hdmap 37084 |
. . 3
 HDMap HDMap           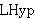                      
             ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                       |
| 38 | | fvex 6201 |
. . . . 5
  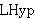      |
| 39 | 3, 38 | eqeltri 2697 |
. . . 4
    |
| 40 | 39 | mptex 6486 |
. . 3
                       
             ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                        |
| 41 | 36, 37, 40 | fvmpt 6282 |
. 2
       HDMap HDMap                
                       ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                       |
| 42 | 1, 41 | syl 17 |
1
       HDMap HDMap                
                       ![]. ].](_drbrack.gif)             ![]. ].](_drbrack.gif)         ![]. ].](_drbrack.gif)    HDMap1 HDMap1        ![]. ].](_drbrack.gif)                 LCDual LCDual          
   
                                           HVMap HVMap                       |