Theorem hgmapfval 37178

Description: Map from the scalar division ring of the vector space to the scalar division ring of its closed kernel dual. (Contributed by NM, 25-Mar-2015.)

Hypotheses

Ref	Expression
hgmapval.h	|- H = ( LHyp ` K )
hgmapfval.u	|- U = ( ( DVecH ` K ) ` W )
hgmapfval.v	|- V = ( Base ` U )
hgmapfval.t	|- .x. = ( .s ` U )
hgmapfval.r	|- R = (Scalar ` U )
hgmapfval.b	|- B = ( Base ` R )
hgmapfval.c	|- C = ( (LCDual ` K ) ` W )
hgmapfval.s	|- .xb = ( .s ` C )
hgmapfval.m	|- M = ( (HDMap ` K ) ` W )
hgmapfval.i	|- I = ( (HGMap ` K ) ` W )
hgmapfval.k	|- ( ph -> ( K e. Y /\ W e. H ) )

Assertion

Ref	Expression
hgmapfval	|- ( ph -> I = ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) )

Distinct variable groups:   x, v, y, K   v, B, x, y   v, M, x, y   v, U, x, y   v, V   v, W, x, y

Allowed substitution hints:   ph( x, y, v)   C( x, y, v)   R( x, y, v)   .xb ( x, y, v)   .x. ( x, y, v)   H( x, y, v)   I( x, y, v)   V( x, y)   Y( x, y, v)

Proof of Theorem hgmapfval

Dummy variables w a b m u are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		hgmapfval.k	. 2 |- ( ph -> ( K e. Y /\ W e. H ) )
2		hgmapfval.i	. . . 4 |- I = ( (HGMap ` K ) ` W )
3		hgmapval.h	. . . . . 6 |- H = ( LHyp ` K )
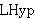4	3	hgmapffval 37177	. . . . 5 |- ( K e. Y -> (HGMap ` K ) = ( w e. H |-> { a | [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) } ) )
5	4	fveq1d 6193	. . . 4 |- ( K e. Y -> ( (HGMap ` K ) ` W ) = ( ( w e. H |-> { a | [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) } ) ` W ) )
6	2, 5	syl5eq 2668	. . 3 |- ( K e. Y -> I = ( ( w e. H |-> { a | [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) } ) ` W ) )
7		fveq2 6191	. . . . . . . 8 |- ( w = W -> ( ( DVecH ` K ) ` w ) = ( ( DVecH ` K ) ` W ) )
8		hgmapfval.u	. . . . . . . 8 |- U = ( ( DVecH ` K ) ` W )
9	7, 8	syl6eqr 2674	. . . . . . 7 |- ( w = W -> ( ( DVecH ` K ) ` w ) = U )
10		fveq2 6191	. . . . . . . . . 10 |- ( w = W -> ( (HDMap ` K ) ` w ) = ( (HDMap ` K ) ` W ) )
11		hgmapfval.m	. . . . . . . . . 10 |- M = ( (HDMap ` K ) ` W )
12	10, 11	syl6eqr 2674	. . . . . . . . 9 |- ( w = W -> ( (HDMap ` K ) ` w ) = M )
13		fveq2 6191	. . . . . . . . . . . . . . . 16 |- ( w = W -> ( (LCDual ` K ) ` w ) = ( (LCDual ` K ) ` W ) )
14	13	fveq2d 6195	. . . . . . . . . . . . . . 15 |- ( w = W -> ( .s ` ( (LCDual ` K ) ` w ) ) = ( .s ` ( (LCDual ` K ) ` W ) ) )
15	14	oveqd 6667	. . . . . . . . . . . . . 14 |- ( w = W -> ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) )
16	15	eqeq2d 2632	. . . . . . . . . . . . 13 |- ( w = W -> ( ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) <-> ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) )
17	16	ralbidv 2986	. . . . . . . . . . . 12 |- ( w = W -> ( A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) <-> A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) )
18	17	riotabidv 6613	. . . . . . . . . . 11 |- ( w = W -> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) = ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) )
19	18	mpteq2dv 4745	. . . . . . . . . 10 |- ( w = W -> ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) = ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) )
20	19	eleq2d 2687	. . . . . . . . 9 |- ( w = W -> ( a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) <-> a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) ) )
21	12, 20	sbceqbid 3442	. . . . . . . 8 |- ( w = W -> ( [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) <-> [. M / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) ) )
22	21	sbcbidv 3490	. . . . . . 7 |- ( w = W -> ( [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) <-> [. ( Base ` (Scalar ` u ) ) / b ]. [. M / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) ) )
23	9, 22	sbceqbid 3442	. . . . . 6 |- ( w = W -> ( [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) <-> [. U / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. M / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) ) )
24		fvex 6201	. . . . . . . 8 |- ( ( DVecH ` K ) ` W ) e. _V
25	8, 24	eqeltri 2697	. . . . . . 7 |- U e. _V
26		fvex 6201	. . . . . . 7 |- ( Base ` (Scalar ` u ) ) e. _V
27		fvex 6201	. . . . . . . 8 |- ( (HDMap ` K ) ` W ) e. _V
28	11, 27	eqeltri 2697	. . . . . . 7 |- M e. _V
29		simp2 1062	. . . . . . . . . 10 |- ( ( u = U /\ b = ( Base ` (Scalar ` u ) ) /\ m = M ) -> b = ( Base ` (Scalar ` u ) ) )
30		simp1 1061	. . . . . . . . . . . . 13 |- ( ( u = U /\ b = ( Base ` (Scalar ` u ) ) /\ m = M ) -> u = U )
31	30	fveq2d 6195	. . . . . . . . . . . 12 |- ( ( u = U /\ b = ( Base ` (Scalar ` u ) ) /\ m = M ) -> (Scalar ` u ) = (Scalar ` U ) )
32		hgmapfval.r	. . . . . . . . . . . 12 |- R = (Scalar ` U )
33	31, 32	syl6eqr 2674	. . . . . . . . . . 11 |- ( ( u = U /\ b = ( Base ` (Scalar ` u ) ) /\ m = M ) -> (Scalar ` u ) = R )
34	33	fveq2d 6195	. . . . . . . . . 10 |- ( ( u = U /\ b = ( Base ` (Scalar ` u ) ) /\ m = M ) -> ( Base ` (Scalar ` u ) ) = ( Base ` R ) )
35	29, 34	eqtrd 2656	. . . . . . . . 9 |- ( ( u = U /\ b = ( Base ` (Scalar ` u ) ) /\ m = M ) -> b = ( Base ` R ) )
36		hgmapfval.b	. . . . . . . . 9 |- B = ( Base ` R )
37	35, 36	syl6eqr 2674	. . . . . . . 8 |- ( ( u = U /\ b = ( Base ` (Scalar ` u ) ) /\ m = M ) -> b = B )
38		simp2 1062	. . . . . . . . . 10 |- ( ( u = U /\ b = B /\ m = M ) -> b = B )
39		simp1 1061	. . . . . . . . . . . . . 14 |- ( ( u = U /\ b = B /\ m = M ) -> u = U )
40	39	fveq2d 6195	. . . . . . . . . . . . 13 |- ( ( u = U /\ b = B /\ m = M ) -> ( Base ` u ) = ( Base ` U ) )
41		hgmapfval.v	. . . . . . . . . . . . 13 |- V = ( Base ` U )
42	40, 41	syl6eqr 2674	. . . . . . . . . . . 12 |- ( ( u = U /\ b = B /\ m = M ) -> ( Base ` u ) = V )
43		simp3 1063	. . . . . . . . . . . . . 14 |- ( ( u = U /\ b = B /\ m = M ) -> m = M )
44	39	fveq2d 6195	. . . . . . . . . . . . . . . 16 |- ( ( u = U /\ b = B /\ m = M ) -> ( .s ` u ) = ( .s ` U ) )
45		hgmapfval.t	. . . . . . . . . . . . . . . 16 |- .x. = ( .s ` U )
46	44, 45	syl6eqr 2674	. . . . . . . . . . . . . . 15 |- ( ( u = U /\ b = B /\ m = M ) -> ( .s ` u ) = .x. )
47	46	oveqd 6667	. . . . . . . . . . . . . 14 |- ( ( u = U /\ b = B /\ m = M ) -> ( x ( .s ` u ) v ) = ( x .x. v ) )
48	43, 47	fveq12d 6197	. . . . . . . . . . . . 13 |- ( ( u = U /\ b = B /\ m = M ) -> ( m ` ( x ( .s ` u ) v ) ) = ( M ` ( x .x. v ) ) )
49		eqidd 2623	. . . . . . . . . . . . . . . . 17 |- ( ( u = U /\ b = B /\ m = M ) -> ( (LCDual ` K ) ` W ) = ( (LCDual ` K ) ` W ) )
50		hgmapfval.c	. . . . . . . . . . . . . . . . 17 |- C = ( (LCDual ` K ) ` W )
51	49, 50	syl6eqr 2674	. . . . . . . . . . . . . . . 16 |- ( ( u = U /\ b = B /\ m = M ) -> ( (LCDual ` K ) ` W ) = C )
52	51	fveq2d 6195	. . . . . . . . . . . . . . 15 |- ( ( u = U /\ b = B /\ m = M ) -> ( .s ` ( (LCDual ` K ) ` W ) ) = ( .s ` C ) )
53		hgmapfval.s	. . . . . . . . . . . . . . 15 |- .xb = ( .s ` C )
54	52, 53	syl6eqr 2674	. . . . . . . . . . . . . 14 |- ( ( u = U /\ b = B /\ m = M ) -> ( .s ` ( (LCDual ` K ) ` W ) ) = .xb )
55		eqidd 2623	. . . . . . . . . . . . . 14 |- ( ( u = U /\ b = B /\ m = M ) -> y = y )
56	43	fveq1d 6193	. . . . . . . . . . . . . 14 |- ( ( u = U /\ b = B /\ m = M ) -> ( m ` v ) = ( M ` v ) )
57	54, 55, 56	oveq123d 6671	. . . . . . . . . . . . 13 |- ( ( u = U /\ b = B /\ m = M ) -> ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) = ( y .xb ( M ` v ) ) )
58	48, 57	eqeq12d 2637	. . . . . . . . . . . 12 |- ( ( u = U /\ b = B /\ m = M ) -> ( ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) <-> ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) )
59	42, 58	raleqbidv 3152	. . . . . . . . . . 11 |- ( ( u = U /\ b = B /\ m = M ) -> ( A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) <-> A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) )
60	38, 59	riotaeqbidv 6614	. . . . . . . . . 10 |- ( ( u = U /\ b = B /\ m = M ) -> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) = ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) )
61	38, 60	mpteq12dv 4733	. . . . . . . . 9 |- ( ( u = U /\ b = B /\ m = M ) -> ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) = ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) )
62	61	eleq2d 2687	. . . . . . . 8 |- ( ( u = U /\ b = B /\ m = M ) -> ( a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) <-> a e. ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) ) )
63	37, 62	syld3an2 1373	. . . . . . 7 |- ( ( u = U /\ b = ( Base ` (Scalar ` u ) ) /\ m = M ) -> ( a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) <-> a e. ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) ) )
64	25, 26, 28, 63	sbc3ie 3507	. . . . . 6 |- ( [. U / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. M / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` W ) ) ( m ` v ) ) ) ) <-> a e. ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) )
65	23, 64	syl6bb 276	. . . . 5 |- ( w = W -> ( [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) <-> a e. ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) ) )
66	65	abbi1dv 2743	. . . 4 |- ( w = W -> { a | [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) } = ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) )
67		eqid 2622	. . . 4 |- ( w e. H |-> { a | [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) } ) = ( w e. H |-> { a | [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) } )
68		fvex 6201	. . . . . 6 |- ( Base ` R ) e. _V
69	36, 68	eqeltri 2697	. . . . 5 |- B e. _V
70	69	mptex 6486	. . . 4 |- ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) e. _V
71	66, 67, 70	fvmpt 6282	. . 3 |- ( W e. H -> ( ( w e. H |-> { a | [. ( ( DVecH ` K ) ` w ) / u ]. [. ( Base ` (Scalar ` u ) ) / b ]. [. ( (HDMap ` K ) ` w ) / m ]. a e. ( x e. b |-> ( iota_ y e. b A. v e. ( Base ` u ) ( m ` ( x ( .s ` u ) v ) ) = ( y ( .s ` ( (LCDual ` K ) ` w ) ) ( m ` v ) ) ) ) } ) ` W ) = ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) )
72	6, 71	sylan9eq 2676	. 2 |- ( ( K e. Y /\ W e. H ) -> I = ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) )
73	1, 72	syl 17	1 |- ( ph -> I = ( x e. B |-> ( iota_ y e. B A. v e. V ( M ` ( x .x. v ) ) = ( y .xb ( M ` v ) ) ) ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   {cab 2608   A.wral 2912   _Vcvv 3200   [.wsbc 3435   |-> cmpt 4729   ` cfv 5888   iota_crio 6610  (class class class)co 6650   Basecbs 15857  Scalarcsca 15944   .scvsca 15945   LHypclh 35270   DVecHcdvh 36367  LCDualclcd 36875  HDMapchdma 37082  HGMapchg 37175

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pr 4906

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-ral 2917  df-rex 2918  df-reu 2919  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-hgmap 37176

This theorem is referenced by:  hgmapval  37179  hgmapfnN  37180