Theorem 2ndconst 5863

Description: The mapping of a restriction of the 2nd function to a converse constant function. (Contributed by NM, 27-Mar-2008.)

Assertion

Ref	Expression
2ndconst	|- ( A e. V -> ( 2nd |` ( { A } X. B ) ) : ( { A } X. B ) -1-1-onto-> B )

Proof of Theorem 2ndconst

Dummy variables x y are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		snmg 3508	. . 3 |- ( A e. V -> E. x x e. { A } )
2		fo2ndresm 5809	. . 3 |- ( E. x x e. { A } -> ( 2nd |` ( { A } X. B ) ) : ( { A } X. B ) -onto-> B )
3	1, 2	syl 14	. 2 |- ( A e. V -> ( 2nd |` ( { A } X. B ) ) : ( { A } X. B ) -onto-> B )
4		moeq 2767	. . . . . 6 |- E* x x = <. A , y >.
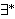
5	4	moani 2011	. . . . 5 |- E* x ( y e. B /\ x = <. A , y >. )
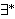
6		vex 2604	. . . . . . . 8 |- y e. _V
7	6	brres 4636	. . . . . . 7 |- ( x ( 2nd |` ( { A } X. B ) ) y <-> ( x 2nd y /\ x e. ( { A } X. B ) ) )
8		fo2nd 5805	. . . . . . . . . . 11 |- 2nd : _V -onto-> _V
9		fofn 5128	. . . . . . . . . . 11 |- ( 2nd : _V -onto-> _V -> 2nd Fn _V )
10	8, 9	ax-mp 7	. . . . . . . . . 10 |- 2nd Fn _V
11		vex 2604	. . . . . . . . . 10 |- x e. _V
12		fnbrfvb 5235	. . . . . . . . . 10 |- ( ( 2nd Fn _V /\ x e. _V ) -> ( ( 2nd ` x ) = y <-> x 2nd y ) )
13	10, 11, 12	mp2an 416	. . . . . . . . 9 |- ( ( 2nd ` x ) = y <-> x 2nd y )
14	13	anbi1i 445	. . . . . . . 8 |- ( ( ( 2nd ` x ) = y /\ x e. ( { A } X. B ) ) <-> ( x 2nd y /\ x e. ( { A } X. B ) ) )
15		elxp7 5817	. . . . . . . . . . 11 |- ( x e. ( { A } X. B ) <-> ( x e. ( _V X. _V ) /\ ( ( 1st ` x ) e. { A } /\ ( 2nd ` x ) e. B ) ) )
16		eleq1 2141	. . . . . . . . . . . . . . 15 |- ( ( 2nd ` x ) = y -> ( ( 2nd ` x ) e. B <-> y e. B ) )
17	16	biimpa 290	. . . . . . . . . . . . . 14 |- ( ( ( 2nd ` x ) = y /\ ( 2nd ` x ) e. B ) -> y e. B )
18	17	adantrl 461	. . . . . . . . . . . . 13 |- ( ( ( 2nd ` x ) = y /\ ( ( 1st ` x ) e. { A } /\ ( 2nd ` x ) e. B ) ) -> y e. B )
19	18	adantrl 461	. . . . . . . . . . . 12 |- ( ( ( 2nd ` x ) = y /\ ( x e. ( _V X. _V ) /\ ( ( 1st ` x ) e. { A } /\ ( 2nd ` x ) e. B ) ) ) -> y e. B )
20		elsni 3416	. . . . . . . . . . . . . 14 |- ( ( 1st ` x ) e. { A } -> ( 1st ` x ) = A )
21		eqopi 5818	. . . . . . . . . . . . . . . 16 |- ( ( x e. ( _V X. _V ) /\ ( ( 1st ` x ) = A /\ ( 2nd ` x ) = y ) ) -> x = <. A , y >. )
22	21	ancom2s 530	. . . . . . . . . . . . . . 15 |- ( ( x e. ( _V X. _V ) /\ ( ( 2nd ` x ) = y /\ ( 1st ` x ) = A ) ) -> x = <. A , y >. )
23	22	an12s 529	. . . . . . . . . . . . . 14 |- ( ( ( 2nd ` x ) = y /\ ( x e. ( _V X. _V ) /\ ( 1st ` x ) = A ) ) -> x = <. A , y >. )
24	20, 23	sylanr2 397	. . . . . . . . . . . . 13 |- ( ( ( 2nd ` x ) = y /\ ( x e. ( _V X. _V ) /\ ( 1st ` x ) e. { A } ) ) -> x = <. A , y >. )
25	24	adantrrr 470	. . . . . . . . . . . 12 |- ( ( ( 2nd ` x ) = y /\ ( x e. ( _V X. _V ) /\ ( ( 1st ` x ) e. { A } /\ ( 2nd ` x ) e. B ) ) ) -> x = <. A , y >. )
26	19, 25	jca 300	. . . . . . . . . . 11 |- ( ( ( 2nd ` x ) = y /\ ( x e. ( _V X. _V ) /\ ( ( 1st ` x ) e. { A } /\ ( 2nd ` x ) e. B ) ) ) -> ( y e. B /\ x = <. A , y >. ) )
27	15, 26	sylan2b 281	. . . . . . . . . 10 |- ( ( ( 2nd ` x ) = y /\ x e. ( { A } X. B ) ) -> ( y e. B /\ x = <. A , y >. ) )
28	27	adantl 271	. . . . . . . . 9 |- ( ( A e. V /\ ( ( 2nd ` x ) = y /\ x e. ( { A } X. B ) ) ) -> ( y e. B /\ x = <. A , y >. ) )
29		fveq2 5198	. . . . . . . . . . . 12 |- ( x = <. A , y >. -> ( 2nd ` x ) = ( 2nd ` <. A , y >. ) )
30		op2ndg 5798	. . . . . . . . . . . . 13 |- ( ( A e. V /\ y e. _V ) -> ( 2nd ` <. A , y >. ) = y )
31	6, 30	mpan2 415	. . . . . . . . . . . 12 |- ( A e. V -> ( 2nd ` <. A , y >. ) = y )
32	29, 31	sylan9eqr 2135	. . . . . . . . . . 11 |- ( ( A e. V /\ x = <. A , y >. ) -> ( 2nd ` x ) = y )
33	32	adantrl 461	. . . . . . . . . 10 |- ( ( A e. V /\ ( y e. B /\ x = <. A , y >. ) ) -> ( 2nd ` x ) = y )
34		simprr 498	. . . . . . . . . . 11 |- ( ( A e. V /\ ( y e. B /\ x = <. A , y >. ) ) -> x = <. A , y >. )
35		snidg 3423	. . . . . . . . . . . . 13 |- ( A e. V -> A e. { A } )
36	35	adantr 270	. . . . . . . . . . . 12 |- ( ( A e. V /\ ( y e. B /\ x = <. A , y >. ) ) -> A e. { A } )
37		simprl 497	. . . . . . . . . . . 12 |- ( ( A e. V /\ ( y e. B /\ x = <. A , y >. ) ) -> y e. B )
38		opelxpi 4394	. . . . . . . . . . . 12 |- ( ( A e. { A } /\ y e. B ) -> <. A , y >. e. ( { A } X. B ) )
39	36, 37, 38	syl2anc 403	. . . . . . . . . . 11 |- ( ( A e. V /\ ( y e. B /\ x = <. A , y >. ) ) -> <. A , y >. e. ( { A } X. B ) )
40	34, 39	eqeltrd 2155	. . . . . . . . . 10 |- ( ( A e. V /\ ( y e. B /\ x = <. A , y >. ) ) -> x e. ( { A } X. B ) )
41	33, 40	jca 300	. . . . . . . . 9 |- ( ( A e. V /\ ( y e. B /\ x = <. A , y >. ) ) -> ( ( 2nd ` x ) = y /\ x e. ( { A } X. B ) ) )
42	28, 41	impbida 560	. . . . . . . 8 |- ( A e. V -> ( ( ( 2nd ` x ) = y /\ x e. ( { A } X. B ) ) <-> ( y e. B /\ x = <. A , y >. ) ) )
43	14, 42	syl5bbr 192	. . . . . . 7 |- ( A e. V -> ( ( x 2nd y /\ x e. ( { A } X. B ) ) <-> ( y e. B /\ x = <. A , y >. ) ) )
44	7, 43	syl5bb 190	. . . . . 6 |- ( A e. V -> ( x ( 2nd |` ( { A } X. B ) ) y <-> ( y e. B /\ x = <. A , y >. ) ) )
45	44	mobidv 1977	. . . . 5 |- ( A e. V -> ( E* x x ( 2nd |` ( { A } X. B ) ) y <-> E* x ( y e. B /\ x = <. A , y >. ) ) )
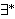
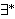46	5, 45	mpbiri 166	. . . 4 |- ( A e. V -> E* x x ( 2nd |` ( { A } X. B ) ) y )
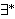47	46	alrimiv 1795	. . 3 |- ( A e. V -> A. y E* x x ( 2nd |` ( { A } X. B ) ) y )
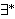
48		funcnv2 4979	. . 3 |- ( Fun `' ( 2nd |` ( { A } X. B ) ) <-> A. y E* x x ( 2nd |` ( { A } X. B ) ) y )
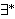
49	47, 48	sylibr 132	. 2 |- ( A e. V -> Fun `' ( 2nd |` ( { A } X. B ) ) )
50		dff1o3 5152	. 2 |- ( ( 2nd |` ( { A } X. B ) ) : ( { A } X. B ) -1-1-onto-> B <-> ( ( 2nd |` ( { A } X. B ) ) : ( { A } X. B ) -onto-> B /\ Fun `' ( 2nd |` ( { A } X. B ) ) ) )
51	3, 49, 50	sylanbrc 408	1 |- ( A e. V -> ( 2nd |` ( { A } X. B ) ) : ( { A } X. B ) -1-1-onto-> B )

Syntax hints:   -> wi 4   /\ wa 102   <-> wb 103   A.wal 1282   = wceq 1284   E.wex 1421   e. wcel 1433   E*wmo 1942   _Vcvv 2601   {csn 3398   <.cop 3401   class class class wbr 3785   X. cxp 4361   `'ccnv 4362   |` cres 4365   Fun wfun 4916   Fn wfn 4917   -onto->wfo 4920   -1-1-onto->wf1o 4921   ` cfv 4922   1stc1st 5785   2ndc2nd 5786

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-13 1444  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-sep 3896  ax-pow 3948  ax-pr 3964  ax-un 4188

This theorem depends on definitions:  df-bi 115  df-3an 921  df-tru 1287  df-nf 1390  df-sb 1686  df-eu 1944  df-mo 1945  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ral 2353  df-rex 2354  df-rab 2357  df-v 2603  df-sbc 2816  df-csb 2909  df-un 2977  df-in 2979  df-ss 2986  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-uni 3602  df-iun 3680  df-br 3786  df-opab 3840  df-mpt 3841  df-id 4048  df-xp 4369  df-rel 4370  df-cnv 4371  df-co 4372  df-dm 4373  df-rn 4374  df-res 4375  df-ima 4376  df-iota 4887  df-fun 4924  df-fn 4925  df-f 4926  df-f1 4927  df-fo 4928  df-f1o 4929  df-fv 4930  df-1st 5787  df-2nd 5788

This theorem is referenced by: (None)