Theorem tfrlemibxssdm 5964

Description: The union of B is defined on all ordinals. Lemma for tfrlemi1 5969. (Contributed by Jim Kingdon, 18-Mar-2019.) (Proof shortened by Mario Carneiro, 24-May-2019.)

Hypotheses

Ref	Expression
tfrlemisucfn.1	|- A = { f | E. x e. On ( f Fn x /\ A. y e. x ( f ` y ) = ( F ` ( f |` y ) ) ) }
tfrlemisucfn.2	|- ( ph -> A. x ( Fun F /\ ( F ` x ) e. _V ) )
tfrlemi1.3	|- B = { h | E. z e. x E. g ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) }
tfrlemi1.4	|- ( ph -> x e. On )
tfrlemi1.5	|- ( ph -> A. z e. x E. g ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) )

Assertion

Ref	Expression
tfrlemibxssdm	|- ( ph -> x C_ dom U. B )

Distinct variable groups:   f, g, h, w, x, y, z, A   f, F, g, h, w, x, y, z   ph, w, y   w, B, f, g, h, z   ph, g, h, z

Allowed substitution hints:   ph( x, f)   B( x, y)

Proof of Theorem tfrlemibxssdm

Step	Hyp	Ref	Expression
1		tfrlemi1.5	. . 3 |- ( ph -> A. z e. x E. g ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) )
2		tfrlemi1.4	. . . 4 |- ( ph -> x e. On )
3		tfrlemisucfn.2	. . . . . . . . . . . 12 |- ( ph -> A. x ( Fun F /\ ( F ` x ) e. _V ) )
4	3	tfrlem3-2d 5951	. . . . . . . . . . 11 |- ( ph -> ( Fun F /\ ( F ` g ) e. _V ) )
5	4	simprd 112	. . . . . . . . . 10 |- ( ph -> ( F ` g ) e. _V )
6	5	3ad2ant1 959	. . . . . . . . 9 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> ( F ` g ) e. _V )
7		vex 2604	. . . . . . . . . . . . 13 |- z e. _V
8		opexg 3983	. . . . . . . . . . . . 13 |- ( ( z e. _V /\ ( F ` g ) e. _V ) -> <. z , ( F ` g ) >. e. _V )
9	7, 5, 8	sylancr 405	. . . . . . . . . . . 12 |- ( ph -> <. z , ( F ` g ) >. e. _V )
10		snidg 3423	. . . . . . . . . . . 12 |- ( <. z , ( F ` g ) >. e. _V -> <. z , ( F ` g ) >. e. { <. z , ( F ` g ) >. } )
11		elun2 3140	. . . . . . . . . . . 12 |- ( <. z , ( F ` g ) >. e. { <. z , ( F ` g ) >. } -> <. z , ( F ` g ) >. e. ( g u. { <. z , ( F ` g ) >. } ) )
12	9, 10, 11	3syl 17	. . . . . . . . . . 11 |- ( ph -> <. z , ( F ` g ) >. e. ( g u. { <. z , ( F ` g ) >. } ) )
13	12	3ad2ant1 959	. . . . . . . . . 10 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> <. z , ( F ` g ) >. e. ( g u. { <. z , ( F ` g ) >. } ) )
14		simp2r 965	. . . . . . . . . . . 12 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> z e. x )
15		simp3l 966	. . . . . . . . . . . 12 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> g Fn z )
16		onelon 4139	. . . . . . . . . . . . . . 15 |- ( ( x e. On /\ z e. x ) -> z e. On )
17		rspe 2412	. . . . . . . . . . . . . . 15 |- ( ( z e. On /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> E. z e. On ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) )
18	16, 17	sylan 277	. . . . . . . . . . . . . 14 |- ( ( ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> E. z e. On ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) )
19		tfrlemisucfn.1	. . . . . . . . . . . . . . 15 |- A = { f | E. x e. On ( f Fn x /\ A. y e. x ( f ` y ) = ( F ` ( f |` y ) ) ) }
20		vex 2604	. . . . . . . . . . . . . . 15 |- g e. _V
21	19, 20	tfrlem3a 5948	. . . . . . . . . . . . . 14 |- ( g e. A <-> E. z e. On ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) )
22	18, 21	sylibr 132	. . . . . . . . . . . . 13 |- ( ( ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> g e. A )
23	22	3adant1 956	. . . . . . . . . . . 12 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> g e. A )
24	14, 15, 23	3jca 1118	. . . . . . . . . . 11 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> ( z e. x /\ g Fn z /\ g e. A ) )
25		snexg 3956	. . . . . . . . . . . . . 14 |- ( <. z , ( F ` g ) >. e. _V -> { <. z , ( F ` g ) >. } e. _V )
26		unexg 4196	. . . . . . . . . . . . . . 15 |- ( ( g e. _V /\ { <. z , ( F ` g ) >. } e. _V ) -> ( g u. { <. z , ( F ` g ) >. } ) e. _V )
27	20, 26	mpan 414	. . . . . . . . . . . . . 14 |- ( { <. z , ( F ` g ) >. } e. _V -> ( g u. { <. z , ( F ` g ) >. } ) e. _V )
28	9, 25, 27	3syl 17	. . . . . . . . . . . . 13 |- ( ph -> ( g u. { <. z , ( F ` g ) >. } ) e. _V )
29		isset 2605	. . . . . . . . . . . . 13 |- ( ( g u. { <. z , ( F ` g ) >. } ) e. _V <-> E. h h = ( g u. { <. z , ( F ` g ) >. } ) )
30	28, 29	sylib 120	. . . . . . . . . . . 12 |- ( ph -> E. h h = ( g u. { <. z , ( F ` g ) >. } ) )
31	30	3ad2ant1 959	. . . . . . . . . . 11 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> E. h h = ( g u. { <. z , ( F ` g ) >. } ) )
32		simpr3 946	. . . . . . . . . . . . . . 15 |- ( ( z e. x /\ ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) ) -> h = ( g u. { <. z , ( F ` g ) >. } ) )
33		19.8a 1522	. . . . . . . . . . . . . . . 16 |- ( ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) -> E. g ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) )
34		rspe 2412	. . . . . . . . . . . . . . . . 17 |- ( ( z e. x /\ E. g ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) ) -> E. z e. x E. g ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) )
35		tfrlemi1.3	. . . . . . . . . . . . . . . . . 18 |- B = { h | E. z e. x E. g ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) }
36	35	abeq2i 2189	. . . . . . . . . . . . . . . . 17 |- ( h e. B <-> E. z e. x E. g ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) )
37	34, 36	sylibr 132	. . . . . . . . . . . . . . . 16 |- ( ( z e. x /\ E. g ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) ) -> h e. B )
38	33, 37	sylan2 280	. . . . . . . . . . . . . . 15 |- ( ( z e. x /\ ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) ) -> h e. B )
39	32, 38	eqeltrrd 2156	. . . . . . . . . . . . . 14 |- ( ( z e. x /\ ( g Fn z /\ g e. A /\ h = ( g u. { <. z , ( F ` g ) >. } ) ) ) -> ( g u. { <. z , ( F ` g ) >. } ) e. B )
40	39	3exp2 1156	. . . . . . . . . . . . 13 |- ( z e. x -> ( g Fn z -> ( g e. A -> ( h = ( g u. { <. z , ( F ` g ) >. } ) -> ( g u. { <. z , ( F ` g ) >. } ) e. B ) ) ) )
41	40	3imp 1132	. . . . . . . . . . . 12 |- ( ( z e. x /\ g Fn z /\ g e. A ) -> ( h = ( g u. { <. z , ( F ` g ) >. } ) -> ( g u. { <. z , ( F ` g ) >. } ) e. B ) )
42	41	exlimdv 1740	. . . . . . . . . . 11 |- ( ( z e. x /\ g Fn z /\ g e. A ) -> ( E. h h = ( g u. { <. z , ( F ` g ) >. } ) -> ( g u. { <. z , ( F ` g ) >. } ) e. B ) )
43	24, 31, 42	sylc 61	. . . . . . . . . 10 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> ( g u. { <. z , ( F ` g ) >. } ) e. B )
44		elunii 3606	. . . . . . . . . 10 |- ( ( <. z , ( F ` g ) >. e. ( g u. { <. z , ( F ` g ) >. } ) /\ ( g u. { <. z , ( F ` g ) >. } ) e. B ) -> <. z , ( F ` g ) >. e. U. B )
45	13, 43, 44	syl2anc 403	. . . . . . . . 9 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> <. z , ( F ` g ) >. e. U. B )
46		opeq2 3571	. . . . . . . . . . . 12 |- ( w = ( F ` g ) -> <. z , w >. = <. z , ( F ` g ) >. )
47	46	eleq1d 2147	. . . . . . . . . . 11 |- ( w = ( F ` g ) -> ( <. z , w >. e. U. B <-> <. z , ( F ` g ) >. e. U. B ) )
48	47	spcegv 2686	. . . . . . . . . 10 |- ( ( F ` g ) e. _V -> ( <. z , ( F ` g ) >. e. U. B -> E. w <. z , w >. e. U. B ) )
49	7	eldm2 4551	. . . . . . . . . 10 |- ( z e. dom U. B <-> E. w <. z , w >. e. U. B )
50	48, 49	syl6ibr 160	. . . . . . . . 9 |- ( ( F ` g ) e. _V -> ( <. z , ( F ` g ) >. e. U. B -> z e. dom U. B ) )
51	6, 45, 50	sylc 61	. . . . . . . 8 |- ( ( ph /\ ( x e. On /\ z e. x ) /\ ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) ) -> z e. dom U. B )
52	51	3expia 1140	. . . . . . 7 |- ( ( ph /\ ( x e. On /\ z e. x ) ) -> ( ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) -> z e. dom U. B ) )
53	52	exlimdv 1740	. . . . . 6 |- ( ( ph /\ ( x e. On /\ z e. x ) ) -> ( E. g ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) -> z e. dom U. B ) )
54	53	anassrs 392	. . . . 5 |- ( ( ( ph /\ x e. On ) /\ z e. x ) -> ( E. g ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) -> z e. dom U. B ) )
55	54	ralimdva 2429	. . . 4 |- ( ( ph /\ x e. On ) -> ( A. z e. x E. g ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) -> A. z e. x z e. dom U. B ) )
56	2, 55	mpdan 412	. . 3 |- ( ph -> ( A. z e. x E. g ( g Fn z /\ A. w e. z ( g ` w ) = ( F ` ( g |` w ) ) ) -> A. z e. x z e. dom U. B ) )
57	1, 56	mpd 13	. 2 |- ( ph -> A. z e. x z e. dom U. B )
58		dfss3 2989	. 2 |- ( x C_ dom U. B <-> A. z e. x z e. dom U. B )
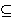
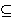
59	57, 58	sylibr 132	1 |- ( ph -> x C_ dom U. B )

Syntax hints:   -> wi 4   /\ wa 102   /\ w3a 919   A.wal 1282   = wceq 1284   E.wex 1421   e. wcel 1433   {cab 2067   A.wral 2348   E.wrex 2349   _Vcvv 2601   u. cun 2971   C_ wss 2973   {csn 3398   <.cop 3401   U.cuni 3601   Oncon0 4118   dom cdm 4363   |` cres 4365   Fun wfun 4916   Fn wfn 4917   ` cfv 4922

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-13 1444  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-sep 3896  ax-pow 3948  ax-pr 3964  ax-un 4188

This theorem depends on definitions:  df-bi 115  df-3an 921  df-tru 1287  df-nf 1390  df-sb 1686  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ral 2353  df-rex 2354  df-v 2603  df-un 2977  df-in 2979  df-ss 2986  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-uni 3602  df-br 3786  df-opab 3840  df-tr 3876  df-iord 4121  df-on 4123  df-xp 4369  df-rel 4370  df-cnv 4371  df-co 4372  df-dm 4373  df-res 4375  df-iota 4887  df-fun 4924  df-fn 4925  df-fv 4930

This theorem is referenced by:  tfrlemibfn  5965