Theorem divalglemeuneg 10323

Description: Lemma for divalg 10324. Uniqueness for a negative denominator. (Contributed by Jim Kingdon, 4-Dec-2021.)

Assertion

Ref	Expression
divalglemeuneg	|- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> E! r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) )

Distinct variable groups:   D, q, r   N, q, r

Proof of Theorem divalglemeuneg

Dummy variables s t are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		simp3 940	. . . 4 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> D < 0 )
2	1	lt0ne0d 7614	. . 3 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> D =/= 0 )
3		divalglemex 10322	. . 3 |- ( ( N e. ZZ /\ D e. ZZ /\ D =/= 0 ) -> E. r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) )
4	2, 3	syld3an3 1214	. 2 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> E. r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) )
5		nfv 1461	. . . . . 6 |- F/ q ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) )
6		nfre1 2407	. . . . . . 7 |- F/ q E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) )
7		nfv 1461	. . . . . . 7 |- F/ q r = s
8	6, 7	nfim 1504	. . . . . 6 |- F/ q ( E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) -> r = s )
9		oveq1 5539	. . . . . . . . . . . 12 |- ( q = t -> ( q x. D ) = ( t x. D ) )
10	9	oveq1d 5547	. . . . . . . . . . 11 |- ( q = t -> ( ( q x. D ) + s ) = ( ( t x. D ) + s ) )
11	10	eqeq2d 2092	. . . . . . . . . 10 |- ( q = t -> ( N = ( ( q x. D ) + s ) <-> N = ( ( t x. D ) + s ) ) )
12	11	3anbi3d 1249	. . . . . . . . 9 |- ( q = t -> ( ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) <-> ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) )
13	12	cbvrexv 2578	. . . . . . . 8 |- ( E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) <-> E. t e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) )
14		simpr 108	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q < t ) -> q < t )
15		simp2 939	. . . . . . . . . . . . . . . . . 18 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> D e. ZZ )
16	15	znegcld 8471	. . . . . . . . . . . . . . . . 17 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> -u D e. ZZ )
17	15	zred 8469	. . . . . . . . . . . . . . . . . . 19 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> D e. RR )
18	17	lt0neg1d 7616	. . . . . . . . . . . . . . . . . 18 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> ( D < 0 <-> 0 < -u D ) )
19	1, 18	mpbid 145	. . . . . . . . . . . . . . . . 17 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> 0 < -u D )
20		elnnz 8361	. . . . . . . . . . . . . . . . 17 |- ( -u D e. NN <-> ( -u D e. ZZ /\ 0 < -u D ) )
21	16, 19, 20	sylanbrc 408	. . . . . . . . . . . . . . . 16 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> -u D e. NN )
22	21	ad5antr 479	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> -u D e. NN )
23		simplrr 502	. . . . . . . . . . . . . . . 16 |- ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) -> s e. ZZ )
24	23	ad3antrrr 475	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> s e. ZZ )
25		simplrl 501	. . . . . . . . . . . . . . . 16 |- ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) -> r e. ZZ )
26	25	ad3antrrr 475	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> r e. ZZ )
27		simplr 496	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> t e. ZZ )
28	27	znegcld 8471	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> -u t e. ZZ )
29		simpr 108	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) -> q e. ZZ )
30	29	ad3antrrr 475	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> q e. ZZ )
31	30	znegcld 8471	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> -u q e. ZZ )
32		simpr1 944	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) -> 0 <_ r )
33	32	ad2antrr 471	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> 0 <_ r )
34		simpr2 945	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> s < ( abs ` D ) )
35		simpll2 978	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) -> D e. ZZ )
36	35	ad3antrrr 475	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> D e. ZZ )
37	36	zred 8469	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> D e. RR )
38		0red 7120	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> 0 e. RR )
39		simpll3 979	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) -> D < 0 )
40	39	ad3antrrr 475	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> D < 0 )
41	37, 38, 40	ltled 7228	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> D <_ 0 )
42	37, 41	absnidd 10046	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( abs ` D ) = -u D )
43	34, 42	breqtrd 3809	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> s < -u D )
44		simpr3 946	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> N = ( ( t x. D ) + s ) )
45	27	zcnd 8470	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> t e. CC )
46	36	zcnd 8470	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> D e. CC )
47	45, 46	mul2negd 7517	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( -u t x. -u D ) = ( t x. D ) )
48	47	oveq1d 5547	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( ( -u t x. -u D ) + s ) = ( ( t x. D ) + s ) )
49	44, 48	eqtr4d 2116	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> N = ( ( -u t x. -u D ) + s ) )
50		simpr3 946	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) -> N = ( ( q x. D ) + r ) )
51	50	ad2antrr 471	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> N = ( ( q x. D ) + r ) )
52	30	zcnd 8470	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> q e. CC )
53	52, 46	mul2negd 7517	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( -u q x. -u D ) = ( q x. D ) )
54	53	oveq1d 5547	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( ( -u q x. -u D ) + r ) = ( ( q x. D ) + r ) )
55	51, 54	eqtr4d 2116	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> N = ( ( -u q x. -u D ) + r ) )
56	49, 55	eqtr3d 2115	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( ( -u t x. -u D ) + s ) = ( ( -u q x. -u D ) + r ) )
57	22, 24, 26, 28, 31, 33, 43, 56	divalglemnqt 10320	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> -. -u t < -u q )
58	30	zred 8469	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> q e. RR )
59	27	zred 8469	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> t e. RR )
60	58, 59	ltnegd 7623	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( q < t <-> -u t < -u q ) )
61	57, 60	mtbird 630	. . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> -. q < t )
62	61	adantr 270	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q < t ) -> -. q < t )
63	14, 62	pm2.21dd 582	. . . . . . . . . . 11 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q < t ) -> r = s )
64	36	adantr 270	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> D e. ZZ )
65	26	adantr 270	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> r e. ZZ )
66	24	adantr 270	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> s e. ZZ )
67	30	adantr 270	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> q e. ZZ )
68	27	adantr 270	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> t e. ZZ )
69		simpr 108	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> q = t )
70	51	adantr 270	. . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> N = ( ( q x. D ) + r ) )
71	44	adantr 270	. . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> N = ( ( t x. D ) + s ) )
72	70, 71	eqtr3d 2115	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> ( ( q x. D ) + r ) = ( ( t x. D ) + s ) )
73	64, 65, 66, 67, 68, 69, 72	divalglemqt 10319	. . . . . . . . . . 11 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ q = t ) -> r = s )
74		simpr 108	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ t < q ) -> t < q )
75		simpr1 944	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> 0 <_ s )
76		simpr2 945	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) -> r < ( abs ` D ) )
77	76	ad2antrr 471	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> r < ( abs ` D ) )
78	77, 42	breqtrd 3809	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> r < -u D )
79	55, 49	eqtr3d 2115	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( ( -u q x. -u D ) + r ) = ( ( -u t x. -u D ) + s ) )
80	22, 26, 24, 31, 28, 75, 78, 79	divalglemnqt 10320	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> -. -u q < -u t )
81	59, 58	ltnegd 7623	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( t < q <-> -u q < -u t ) )
82	80, 81	mtbird 630	. . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> -. t < q )
83	82	adantr 270	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ t < q ) -> -. t < q )
84	74, 83	pm2.21dd 582	. . . . . . . . . . 11 |- ( ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) /\ t < q ) -> r = s )
85		simplr 496	. . . . . . . . . . . . 13 |- ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) -> q e. ZZ )
86	85	ad2antrr 471	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> q e. ZZ )
87		ztri3or 8394	. . . . . . . . . . . 12 |- ( ( q e. ZZ /\ t e. ZZ ) -> ( q < t \/ q = t \/ t < q ) )
88	86, 27, 87	syl2anc 403	. . . . . . . . . . 11 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> ( q < t \/ q = t \/ t < q ) )
89	63, 73, 84, 88	mpjao3dan 1238	. . . . . . . . . 10 |- ( ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) /\ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) ) -> r = s )
90	89	ex 113	. . . . . . . . 9 |- ( ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) /\ t e. ZZ ) -> ( ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) -> r = s ) )
91	90	rexlimdva 2477	. . . . . . . 8 |- ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) -> ( E. t e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( t x. D ) + s ) ) -> r = s ) )
92	13, 91	syl5bi 150	. . . . . . 7 |- ( ( ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) /\ q e. ZZ ) /\ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) -> ( E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) -> r = s ) )
93	92	exp31 356	. . . . . 6 |- ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) -> ( q e. ZZ -> ( ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) -> ( E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) -> r = s ) ) ) )
94	5, 8, 93	rexlimd 2474	. . . . 5 |- ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) -> ( E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) -> ( E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) -> r = s ) ) )
95	94	impd 251	. . . 4 |- ( ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) /\ ( r e. ZZ /\ s e. ZZ ) ) -> ( ( E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) /\ E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) ) -> r = s ) )
96	95	ralrimivva 2443	. . 3 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> A. r e. ZZ A. s e. ZZ ( ( E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) /\ E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) ) -> r = s ) )
97		breq2 3789	. . . . . 6 |- ( r = s -> ( 0 <_ r <-> 0 <_ s ) )
98		breq1 3788	. . . . . 6 |- ( r = s -> ( r < ( abs ` D ) <-> s < ( abs ` D ) ) )
99		oveq2 5540	. . . . . . 7 |- ( r = s -> ( ( q x. D ) + r ) = ( ( q x. D ) + s ) )
100	99	eqeq2d 2092	. . . . . 6 |- ( r = s -> ( N = ( ( q x. D ) + r ) <-> N = ( ( q x. D ) + s ) ) )
101	97, 98, 100	3anbi123d 1243	. . . . 5 |- ( r = s -> ( ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) <-> ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) ) )
102	101	rexbidv 2369	. . . 4 |- ( r = s -> ( E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) <-> E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) ) )
103	102	rmo4 2785	. . 3 |- ( E* r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) <-> A. r e. ZZ A. s e. ZZ ( ( E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) /\ E. q e. ZZ ( 0 <_ s /\ s < ( abs ` D ) /\ N = ( ( q x. D ) + s ) ) ) -> r = s ) )
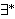
104	96, 103	sylibr 132	. 2 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> E* r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) )
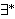
105		reu5 2566	. 2 |- ( E! r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) <-> ( E. r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) /\ E* r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) ) )
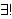
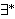
106	4, 104, 105	sylanbrc 408	1 |- ( ( N e. ZZ /\ D e. ZZ /\ D < 0 ) -> E! r e. ZZ E. q e. ZZ ( 0 <_ r /\ r < ( abs ` D ) /\ N = ( ( q x. D ) + r ) ) )

Syntax hints:   -. wn 3   -> wi 4   /\ wa 102   \/ w3o 918   /\ w3a 919   = wceq 1284   e. wcel 1433   =/= wne 2245   A.wral 2348   E.wrex 2349   E!wreu 2350   E*wrmo 2351   class class class wbr 3785   ` cfv 4922  (class class class)co 5532   0cc0 6981   + caddc 6984   x. cmul 6986   < clt 7153   <_ cle 7154   -ucneg 7280   NNcn 8039   ZZcz 8351   abscabs 9883

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-in1 576  ax-in2 577  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-13 1444  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-coll 3893  ax-sep 3896  ax-nul 3904  ax-pow 3948  ax-pr 3964  ax-un 4188  ax-setind 4280  ax-iinf 4329  ax-cnex 7067  ax-resscn 7068  ax-1cn 7069  ax-1re 7070  ax-icn 7071  ax-addcl 7072  ax-addrcl 7073  ax-mulcl 7074  ax-mulrcl 7075  ax-addcom 7076  ax-mulcom 7077  ax-addass 7078  ax-mulass 7079  ax-distr 7080  ax-i2m1 7081  ax-0lt1 7082  ax-1rid 7083  ax-0id 7084  ax-rnegex 7085  ax-precex 7086  ax-cnre 7087  ax-pre-ltirr 7088  ax-pre-ltwlin 7089  ax-pre-lttrn 7090  ax-pre-apti 7091  ax-pre-ltadd 7092  ax-pre-mulgt0 7093  ax-pre-mulext 7094  ax-arch 7095

This theorem depends on definitions:  df-bi 115  df-dc 776  df-3or 920  df-3an 921  df-tru 1287  df-fal 1290  df-nf 1390  df-sb 1686  df-eu 1944  df-mo 1945  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ne 2246  df-nel 2340  df-ral 2353  df-rex 2354  df-reu 2355  df-rmo 2356  df-rab 2357  df-v 2603  df-sbc 2816  df-csb 2909  df-dif 2975  df-un 2977  df-in 2979  df-ss 2986  df-nul 3252  df-if 3352  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-uni 3602  df-int 3637  df-iun 3680  df-br 3786  df-opab 3840  df-mpt 3841  df-tr 3876  df-id 4048  df-po 4051  df-iso 4052  df-iord 4121  df-on 4123  df-suc 4126  df-iom 4332  df-xp 4369  df-rel 4370  df-cnv 4371  df-co 4372  df-dm 4373  df-rn 4374  df-res 4375  df-ima 4376  df-iota 4887  df-fun 4924  df-fn 4925  df-f 4926  df-f1 4927  df-fo 4928  df-f1o 4929  df-fv 4930  df-riota 5488  df-ov 5535  df-oprab 5536  df-mpt2 5537  df-1st 5787  df-2nd 5788  df-recs 5943  df-frec 6001  df-pnf 7155  df-mnf 7156  df-xr 7157  df-ltxr 7158  df-le 7159  df-sub 7281  df-neg 7282  df-reap 7675  df-ap 7682  df-div 7761  df-inn 8040  df-2 8098  df-n0 8289  df-z 8352  df-uz 8620  df-q 8705  df-rp 8735  df-fl 9274  df-mod 9325  df-iseq 9432  df-iexp 9476  df-cj 9729  df-re 9730  df-im 9731  df-rsqrt 9884  df-abs 9885

This theorem is referenced by:  divalg  10324