| Step | Hyp | Ref
| Expression |
|---|
| 1 | | simplr 792 |
. 2
      CRingOps CRingOps         
  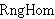             
  |
| 2 | | foelrn 6378 |
. . . . . . . 8
         
   
   
        |
| 3 | 2 | ex 450 |
. . . . . . 7
                  
       |
| 4 | | foelrn 6378 |
. . . . . . . 8
         
   
   
        |
| 5 | 4 | ex 450 |
. . . . . . 7
                  
       |
| 6 | 3, 5 | anim12d 586 |
. . . . . 6
                     
   
        
           |
| 7 | | reeanv 3107 |
. . . . . 6
        
           
      
   
           
          |
| 8 | 6, 7 | syl6ibr 242 |
. . . . 5
                      
   
                   |
| 9 | 8 | ad2antll 765 |
. . . 4
      CRingOps CRingOps         
  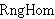                          
   
                   |
| 10 | | crnghomfo.1 |
. . . . . . . . . . . . . 14
        |
| 11 | | eqid 2622 |
. . . . . . . . . . . . . 14
            |
| 12 | | crnghomfo.2 |
. . . . . . . . . . . . . 14
     |
| 13 | 10, 11, 12 | crngocom 33800 |
. . . . . . . . . . . . 13
     CRingOps CRingOps
   
                          |
| 14 | 13 | 3expb 1266 |
. . . . . . . . . . . 12
     CRingOps CRingOps
       
   
                    |
| 15 | 14 | 3ad2antl1 1223 |
. . . . . . . . . . 11
      CRingOps CRingOps     
   
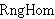                                    |
| 16 | 15 | fveq2d 6195 |
. . . . . . . . . 10
      CRingOps CRingOps     
   
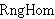                                            |
| 17 | | crngorngo 33799 |
. . . . . . . . . . 11
    CRingOps CRingOps      |
| 18 | | eqid 2622 |
. . . . . . . . . . . 12
            |
| 19 | 10, 12, 11, 18 | rngohommul 33769 |
. . . . . . . . . . 11
         
      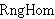                                                |
| 20 | 17, 19 | syl3anl1 1374 |
. . . . . . . . . 10
      CRingOps CRingOps     
   
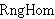                                                |
| 21 | 10, 12, 11, 18 | rngohommul 33769 |
. . . . . . . . . . . 12
         
      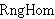                                                |
| 22 | 21 | ancom2s 844 |
. . . . . . . . . . 11
         
      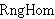                                                |
| 23 | 17, 22 | syl3anl1 1374 |
. . . . . . . . . 10
      CRingOps CRingOps     
   
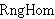                                                |
| 24 | 16, 20, 23 | 3eqtr3d 2664 |
. . . . . . . . 9
      CRingOps CRingOps     
   
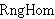                                                    |
| 25 | | oveq12 6659 |
. . . . . . . . . 10
            
                                   |
| 26 | | oveq12 6659 |
. . . . . . . . . . 11
            
                                   |
| 27 | 26 | ancoms 469 |
. . . . . . . . . 10
            
                                   |
| 28 | 25, 27 | eqeq12d 2637 |
. . . . . . . . 9
            
                           
                                     |
| 29 | 24, 28 | syl5ibrcom 237 |
. . . . . . . 8
      CRingOps CRingOps     
   
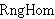                         
        
                     |
| 30 | 29 | ex 450 |
. . . . . . 7
     CRingOps CRingOps
         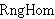                                  
                      |
| 31 | 30 | 3expa 1265 |
. . . . . 6
      CRingOps CRingOps           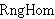    
       
            
        
                      |
| 32 | 31 | adantrr 753 |
. . . . 5
      CRingOps CRingOps         
  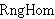                                         
                      |
| 33 | 32 | rexlimdvv 3037 |
. . . 4
      CRingOps CRingOps         
  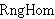                             
        
                     |
| 34 | 9, 33 | syld 47 |
. . 3
      CRingOps CRingOps         
  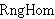                                            |
| 35 | 34 | ralrimivv 2970 |
. 2
      CRingOps CRingOps         
  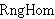             
   
                      |
| 36 | | crnghomfo.3 |
. . 3
        |
| 37 | | crnghomfo.4 |
. . 3
     |
| 38 | 36, 18, 37 | iscrngo2 33796 |
. 2
    CRingOps CRingOps             
                      |
| 39 | 1, 35, 38 | sylanbrc 698 |
1
      CRingOps CRingOps         
  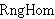              CRingOps
CRingOps |