MPE Home Metamath Proof Explorer < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  MPE Home  >  Th. List  >  iunocv Structured version   Visualization version   Unicode version
Theorem iunocv 20025
Description: The orthocomplement of an indexed union. (Contributed by Mario Carneiro, 23-Oct-2015.)
Hypotheses
Ref Expression
inocv.o |- ._|_ = ( ocv ` W )
iunocv.v |- V = ( Base ` W )
Assertion
Ref Expression
iunocv |- ( ._|_ ` U_ x e. A B ) = ( V i^i |^|_ x e. A ( ._|_ ` B ) )
Distinct variable groups:   x, V   x, W
Allowed substitution hints:   A( x)   B( x)   ._|_ ( x)
Proof of Theorem iunocv
Dummy variables y z are mutually distinct and distinct from all other variables.
StepHypRef Expression
1 iunss 4561 . . . . . . 7 |- ( U_ x e. A B C_ V <-> A. x e. A B C_ V )
2 eliun 4524 . . . . . . . . . . 11 |- ( y e. U_ x e. A B <-> E. x e. A y e. B )
32imbi1i 339 . . . . . . . . . 10 |- ( ( y e. U_ x e. A B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> ( E. x e. A y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
4 r19.23v 3023 . . . . . . . . . 10 |- ( A. x e. A ( y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> ( E. x e. A y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
53, 4bitr4i 267 . . . . . . . . 9 |- ( ( y e. U_ x e. A B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> A. x e. A ( y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
65albii 1747 . . . . . . . 8 |- ( A. y ( y e. U_ x e. A B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> A. y A. x e. A ( y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
7 df-ral 2917 . . . . . . . 8 |- ( A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) <-> A. y ( y e. U_ x e. A B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
8 df-ral 2917 . . . . . . . . . 10 |- ( A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) <-> A. y ( y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
98ralbii 2980 . . . . . . . . 9 |- ( A. x e. A A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) <-> A. x e. A A. y ( y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
10 ralcom4 3224 . . . . . . . . 9 |- ( A. x e. A A. y ( y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> A. y A. x e. A ( y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
119, 10bitri 264 . . . . . . . 8 |- ( A. x e. A A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) <-> A. y A. x e. A ( y e. B -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
126, 7, 113bitr4i 292 . . . . . . 7 |- ( A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) <-> A. x e. A A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) )
131, 12anbi12i 733 . . . . . 6 |- ( ( U_ x e. A B C_ V /\ A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> ( A. x e. A B C_ V /\ A. x e. A A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
14 r19.26 3064 . . . . . 6 |- ( A. x e. A ( B C_ V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> ( A. x e. A B C_ V /\ A. x e. A A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
1513, 14bitr4i 267 . . . . 5 |- ( ( U_ x e. A B C_ V /\ A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> A. x e. A ( B C_ V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
16 eliin 4525 . . . . . 6 |- ( z e. V -> ( z e. |^|_ x e. A ( ._|_ ` B ) <-> A. x e. A z e. ( ._|_ ` B ) ) )
17 iunocv.v . . . . . . . . . 10 |- V = ( Base ` W )
18 eqid 2622 . . . . . . . . . 10 |- ( .i ` W ) = ( .i ` W )
19 eqid 2622 . . . . . . . . . 10 |- (Scalar ` W ) = (Scalar ` W )
20 eqid 2622 . . . . . . . . . 10 |- ( 0g ` (Scalar ` W ) ) = ( 0g ` (Scalar ` W ) )
21 inocv.o . . . . . . . . . 10 |- ._|_ = ( ocv ` W )
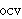2217, 18, 19, 20, 21elocv 20012 . . . . . . . . 9 |- ( z e. ( ._|_ ` B ) <-> ( B C_ V /\ z e. V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
23 3anan12 1051 . . . . . . . . 9 |- ( ( B C_ V /\ z e. V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> ( z e. V /\ ( B C_ V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) ) )
2422, 23bitri 264 . . . . . . . 8 |- ( z e. ( ._|_ ` B ) <-> ( z e. V /\ ( B C_ V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) ) )
2524baib 944 . . . . . . 7 |- ( z e. V -> ( z e. ( ._|_ ` B ) <-> ( B C_ V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) ) )
2625ralbidv 2986 . . . . . 6 |- ( z e. V -> ( A. x e. A z e. ( ._|_ ` B ) <-> A. x e. A ( B C_ V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) ) )
2716, 26bitr2d 269 . . . . 5 |- ( z e. V -> ( A. x e. A ( B C_ V /\ A. y e. B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> z e. |^|_ x e. A ( ._|_ ` B ) ) )
2815, 27syl5bb 272 . . . 4 |- ( z e. V -> ( ( U_ x e. A B C_ V /\ A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> z e. |^|_ x e. A ( ._|_ ` B ) ) )
2928pm5.32i 669 . . 3 |- ( ( z e. V /\ ( U_ x e. A B C_ V /\ A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) ) <-> ( z e. V /\ z e. |^|_ x e. A ( ._|_ ` B ) ) )
3017, 18, 19, 20, 21elocv 20012 . . . 4 |- ( z e. ( ._|_ ` U_ x e. A B ) <-> ( U_ x e. A B C_ V /\ z e. V /\ A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) )
31 3anan12 1051 . . . 4 |- ( ( U_ x e. A B C_ V /\ z e. V /\ A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) <-> ( z e. V /\ ( U_ x e. A B C_ V /\ A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) ) )
3230, 31bitri 264 . . 3 |- ( z e. ( ._|_ ` U_ x e. A B ) <-> ( z e. V /\ ( U_ x e. A B C_ V /\ A. y e. U_ x e. A B ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) ) ) )
33 elin 3796 . . 3 |- ( z e. ( V i^i |^|_ x e. A ( ._|_ ` B ) ) <-> ( z e. V /\ z e. |^|_ x e. A ( ._|_ ` B ) ) )
3429, 32, 333bitr4i 292 . 2 |- ( z e. ( ._|_ ` U_ x e. A B ) <-> z e. ( V i^i |^|_ x e. A ( ._|_ ` B ) ) )
3534eqriv 2619 1 |- ( ._|_ ` U_ x e. A B ) = ( V i^i |^|_ x e. A ( ._|_ ` B ) )
Colors of variables: wff setvar class
Syntax hints:   -> wi 4   /\ wa 384   /\ w3a 1037   A.wal 1481   = wceq 1483   e. wcel 1990   A.wral 2912   E.wrex 2913   i^i cin 3573   C_ wss 3574   U_ciun 4520   |^|_ciin 4521   ` cfv 5888  (class class class)co 6650   Basecbs 15857  Scalarcsca 15944   .icip 15946   0gc0g 16100   ocvcocv 20004
This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949
This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-ral 2917  df-rex 2918  df-rab 2921  df-v 3202  df-sbc 3436  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-fv 5896  df-ov 6653  df-ocv 20007
This theorem is referenced by: (None)
  Copyright terms: Public domain W3C validator