| Step | Hyp | Ref
| Expression |
|---|
| 1 | | caucvgsr.f |
. . . 4
          |
| 2 | | caucvgsr.cau |
. . . 4
                                                 ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)      
      ![] ]](rbrack.gif)                                   ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)          
  ![] ]](rbrack.gif)      |
| 3 | | caucvgsrlemgt1.gt1 |
. . . 4
                |
| 4 | | eqid 2081 |
. . . 4
                           ![] ]](rbrack.gif)                         
     ![] ]](rbrack.gif)    |
| 5 | 1, 2, 3, 4 | caucvgsrlemf 6968 |
. . 3
                        
     ![] ]](rbrack.gif)         |
| 6 | 1, 2, 3, 4 | caucvgsrlemcau 6969 |
. . 3
                                          
  ![] ]](rbrack.gif)                 
            
     ![] ]](rbrack.gif)             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                              
     ![] ]](rbrack.gif)                                    ![] ]](rbrack.gif)                       ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)           |
| 7 | 1, 2, 3, 4 | caucvgsrlembound 6970 |
. . 3
                                     ![] ]](rbrack.gif)        |
| 8 | 5, 6, 7 | caucvgprpr 6902 |
. 2
              
         
                      
     ![] ]](rbrack.gif)             
                           
  ![] ]](rbrack.gif)       
     |
| 9 | | prsrcl 6960 |
. . . 4
                ![] ]](rbrack.gif)     |
| 10 | 9 | ad2antrl 473 |
. . 3
    
                                                  ![] ]](rbrack.gif)          
   
                       
     ![] ]](rbrack.gif)                         ![] ]](rbrack.gif)     |
| 11 | | srpospr 6959 |
. . . . . . . . . 10
            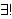 
         
  ![] ]](rbrack.gif)     |
| 12 | | riotacl 5502 |
. . . . . . . . . 10
  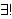           
  ![] ]](rbrack.gif)   
                ![] ]](rbrack.gif)        |
| 13 | 11, 12 | syl 14 |
. . . . . . . . 9
                        
  ![] ]](rbrack.gif)        |
| 14 | 13 | adantll 459 |
. . . . . . . 8
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                     
  ![] ]](rbrack.gif)        |
| 15 | | simplrr 502 |
. . . . . . . . 9
                 
         
                      
     ![] ]](rbrack.gif)             
                           
  ![] ]](rbrack.gif)       
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)             |
| 16 | 15 | adantr 270 |
. . . . . . . 8
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                                      ![] ]](rbrack.gif)          
   
                       
     ![] ]](rbrack.gif)             |
| 17 | | oveq2 5540 |
. . . . . . . . . . . . 13
             
     ![] ]](rbrack.gif)        
                  
  ![] ]](rbrack.gif)       |
| 18 | 17 | breq2d 3797 |
. . . . . . . . . . . 12
             
     ![] ]](rbrack.gif)                               
  ![] ]](rbrack.gif)             
        
            
     ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)        |
| 19 | | oveq2 5540 |
. . . . . . . . . . . . 13
             
     ![] ]](rbrack.gif)                               
  ![] ]](rbrack.gif)       
            
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)       |
| 20 | 19 | breq2d 3797 |
. . . . . . . . . . . 12
             
     ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)          
                           
  ![] ]](rbrack.gif)       
               ![] ]](rbrack.gif)        |
| 21 | 18, 20 | anbi12d 456 |
. . . . . . . . . . 11
             
     ![] ]](rbrack.gif)                                   ![] ]](rbrack.gif)          
   
                       
     ![] ]](rbrack.gif)           
                      
     ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)         |
| 22 | 21 | imbi2d 228 |
. . . . . . . . . 10
             
     ![] ]](rbrack.gif)                                        ![] ]](rbrack.gif)          
   
                       
     ![] ]](rbrack.gif)                                              ![] ]](rbrack.gif)          
               ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)          |
| 23 | 22 | rexralbidv 2392 |
. . . . . . . . 9
             
     ![] ]](rbrack.gif)        
                                    
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)            
            
                      
     ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)          |
| 24 | 23 | rspcva 2699 |
. . . . . . . 8
               
  ![] ]](rbrack.gif)                  
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                    
  ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)         |
| 25 | 14, 16, 24 | syl2anc 403 |
. . . . . . 7
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                     
                      
     ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)         |
| 26 | | nfv 1461 |
. . . . . . . . . . 11
    |
| 27 | | nfv 1461 |
. . . . . . . . . . . 12
      |
| 28 | | nfcv 2219 |
. . . . . . . . . . . . 13
 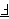   |
| 29 | | nfre1 2407 |
. . . . . . . . . . . . 13
                                         
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)            |
| 30 | 28, 29 | nfralya 2404 |
. . . . . . . . . . . 12
             
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)            |
| 31 | 27, 30 | nfan 1497 |
. . . . . . . . . . 11
                  
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)             |
| 32 | 26, 31 | nfan 1497 |
. . . . . . . . . 10
                 
         
                      
     ![] ]](rbrack.gif)             
                           
  ![] ]](rbrack.gif)       
      |
| 33 | | nfv 1461 |
. . . . . . . . . 10
      |
| 34 | 32, 33 | nfan 1497 |
. . . . . . . . 9
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                   |
| 35 | | nfv 1461 |
. . . . . . . . 9
    
 |
| 36 | 34, 35 | nfan 1497 |
. . . . . . . 8
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                        |
| 37 | | nfv 1461 |
. . . . . . . . . . . 12
    |
| 38 | | nfv 1461 |
. . . . . . . . . . . . 13
      |
| 39 | | nfcv 2219 |
. . . . . . . . . . . . . 14
 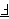   |
| 40 | | nfcv 2219 |
. . . . . . . . . . . . . . 15
 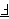   |
| 41 | | nfra1 2397 |
. . . . . . . . . . . . . . 15
                                        ![] ]](rbrack.gif)          
   
                       
     ![] ]](rbrack.gif)            |
| 42 | 40, 41 | nfrexya 2405 |
. . . . . . . . . . . . . 14
                                         
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)            |
| 43 | 39, 42 | nfralya 2404 |
. . . . . . . . . . . . 13
             
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)            |
| 44 | 38, 43 | nfan 1497 |
. . . . . . . . . . . 12
                  
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)             |
| 45 | 37, 44 | nfan 1497 |
. . . . . . . . . . 11
                 
         
                      
     ![] ]](rbrack.gif)             
                           
  ![] ]](rbrack.gif)       
      |
| 46 | | nfv 1461 |
. . . . . . . . . . 11
      |
| 47 | 45, 46 | nfan 1497 |
. . . . . . . . . 10
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                   |
| 48 | | nfv 1461 |
. . . . . . . . . 10
    
 |
| 49 | 47, 48 | nfan 1497 |
. . . . . . . . 9
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                        |
| 50 | 5 | ad4antr 477 |
. . . . . . . . . . . . . 14
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                     
            
     ![] ]](rbrack.gif)         |
| 51 | | simpr 108 |
. . . . . . . . . . . . . 14
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                  |
| 52 | 50, 51 | ffvelrnd 5324 |
. . . . . . . . . . . . 13
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                   
     ![] ]](rbrack.gif)          |
| 53 | | simplrl 501 |
. . . . . . . . . . . . . . . 16
                 
         
                      
     ![] ]](rbrack.gif)             
                           
  ![] ]](rbrack.gif)       
                |
| 54 | 53 | adantr 270 |
. . . . . . . . . . . . . . 15
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                             |
| 55 | | addclpr 6727 |
. . . . . . . . . . . . . . 15
                   
  ![] ]](rbrack.gif)                        
  ![] ]](rbrack.gif)         |
| 56 | 54, 14, 55 | syl2anc 403 |
. . . . . . . . . . . . . 14
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                           
               ![] ]](rbrack.gif)         |
| 57 | 56 | adantr 270 |
. . . . . . . . . . . . 13
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                
               ![] ]](rbrack.gif)         |
| 58 | | prsrlt 6963 |
. . . . . . . . . . . . 13
                           
  ![] ]](rbrack.gif)                         
  ![] ]](rbrack.gif)                                   
  ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)      
                           
  ![] ]](rbrack.gif)       
     ![] ]](rbrack.gif)                     
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)    |
| 59 | 52, 57, 58 | syl2anc 403 |
. . . . . . . . . . . 12
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                       
  ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)      
                           
  ![] ]](rbrack.gif)       
     ![] ]](rbrack.gif)                     
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)    |
| 60 | 1, 2, 3, 4 | caucvgsrlemfv 6967 |
. . . . . . . . . . . . . . . 16
    
   
                            
  ![] ]](rbrack.gif)       
     ![] ]](rbrack.gif)         |
| 61 | 60 | adantlr 460 |
. . . . . . . . . . . . . . 15
                 
         
                      
     ![] ]](rbrack.gif)             
                           
  ![] ]](rbrack.gif)       
                                       
  ![] ]](rbrack.gif)       
     ![] ]](rbrack.gif)         |
| 62 | 61 | adantlr 460 |
. . . . . . . . . . . . . 14
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                    
  ![] ]](rbrack.gif)       
     ![] ]](rbrack.gif)         |
| 63 | 62 | adantlr 460 |
. . . . . . . . . . . . 13
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                         
  ![] ]](rbrack.gif)       
     ![] ]](rbrack.gif)         |
| 64 | | prsradd 6962 |
. . . . . . . . . . . . . . . 16
                   
  ![] ]](rbrack.gif)                           
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)              ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)    |
| 65 | 54, 14, 64 | syl2anc 403 |
. . . . . . . . . . . . . . 15
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                           
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)              ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)    |
| 66 | | prsrriota 6964 |
. . . . . . . . . . . . . . . . 17
                              ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)     |
| 67 | 66 | oveq2d 5548 |
. . . . . . . . . . . . . . . 16
                 
     ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)   
        
  ![] ]](rbrack.gif)      |
| 68 | 67 | adantll 459 |
. . . . . . . . . . . . . . 15
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                    ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)   
        
  ![] ]](rbrack.gif)      |
| 69 | 65, 68 | eqtrd 2113 |
. . . . . . . . . . . . . 14
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                           
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)              ![] ]](rbrack.gif)      |
| 70 | 69 | adantr 270 |
. . . . . . . . . . . . 13
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)              ![] ]](rbrack.gif)      |
| 71 | 63, 70 | breq12d 3798 |
. . . . . . . . . . . 12
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                          
            
     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                     
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)  
                 ![] ]](rbrack.gif)       |
| 72 | 59, 71 | bitrd 186 |
. . . . . . . . . . 11
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                       
  ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)      
                 ![] ]](rbrack.gif)       |
| 73 | 54 | adantr 270 |
. . . . . . . . . . . . 13
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                  |
| 74 | 14 | adantr 270 |
. . . . . . . . . . . . . 14
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                          
  ![] ]](rbrack.gif)        |
| 75 | | addclpr 6727 |
. . . . . . . . . . . . . 14
                           
  ![] ]](rbrack.gif)                      
  ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)         |
| 76 | 52, 74, 75 | syl2anc 403 |
. . . . . . . . . . . . 13
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                       
  ![] ]](rbrack.gif)       
               ![] ]](rbrack.gif)         |
| 77 | | prsrlt 6963 |
. . . . . . . . . . . . 13
                                   ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)                      
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)      
    
     ![] ]](rbrack.gif)               
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)    |
| 78 | 73, 76, 77 | syl2anc 403 |
. . . . . . . . . . . 12
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                          
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)      
    
     ![] ]](rbrack.gif)               
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)    |
| 79 | | prsradd 6962 |
. . . . . . . . . . . . . 14
                           
  ![] ]](rbrack.gif)                      
  ![] ]](rbrack.gif)                                        ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)               
            
     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)    |
| 80 | 52, 74, 79 | syl2anc 403 |
. . . . . . . . . . . . 13
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                             ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)               
            
     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)    |
| 81 | 80 | breq2d 3797 |
. . . . . . . . . . . 12
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                         ![] ]](rbrack.gif)                                  ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)  
    
     ![] ]](rbrack.gif)               
            
     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)     |
| 82 | 66 | adantll 459 |
. . . . . . . . . . . . . . 15
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                        
  ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)     |
| 83 | 82 | adantr 270 |
. . . . . . . . . . . . . 14
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                             
  ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)     |
| 84 | 63, 83 | oveq12d 5550 |
. . . . . . . . . . . . 13
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                          
            
     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)   
          |
| 85 | 84 | breq2d 3797 |
. . . . . . . . . . . 12
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                         ![] ]](rbrack.gif)               
            
     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)        
  ![] ]](rbrack.gif)              ![] ]](rbrack.gif)              |
| 86 | 78, 81, 85 | 3bitrd 212 |
. . . . . . . . . . 11
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                          
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)      
    
     ![] ]](rbrack.gif)              |
| 87 | 72, 86 | anbi12d 456 |
. . . . . . . . . 10
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                           ![] ]](rbrack.gif)          
               ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)                          ![] ]](rbrack.gif)     
    
     ![] ]](rbrack.gif)               |
| 88 | 87 | imbi2d 228 |
. . . . . . . . 9
                       
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                                                ![] ]](rbrack.gif)          
               ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)             
            
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                |
| 89 | 49, 88 | ralbida 2362 |
. . . . . . . 8
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                           
                                   ![] ]](rbrack.gif)          
               ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)                                    ![] ]](rbrack.gif)     
    
     ![] ]](rbrack.gif)                |
| 90 | 36, 89 | rexbid 2367 |
. . . . . . 7
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                           
                                    
  ![] ]](rbrack.gif)                       
  ![] ]](rbrack.gif)                  
            
     ![] ]](rbrack.gif)                    
  ![] ]](rbrack.gif)                                        ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                |
| 91 | 25, 90 | mpbid 145 |
. . . . . 6
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                     
            
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)               |
| 92 | | breq2 3789 |
. . . . . . . . 9
          
     |
| 93 | | fveq2 5198 |
. . . . . . . . . . 11
                  |
| 94 | 93 | breq1d 3795 |
. . . . . . . . . 10
                        ![] ]](rbrack.gif)     
                 ![] ]](rbrack.gif)       |
| 95 | 93 | oveq1d 5547 |
. . . . . . . . . . 11
                          |
| 96 | 95 | breq2d 3797 |
. . . . . . . . . 10
                 ![] ]](rbrack.gif)                       ![] ]](rbrack.gif)              |
| 97 | 94, 96 | anbi12d 456 |
. . . . . . . . 9
                         ![] ]](rbrack.gif)     
    
     ![] ]](rbrack.gif)                          
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)               |
| 98 | 92, 97 | imbi12d 232 |
. . . . . . . 8
                              ![] ]](rbrack.gif)     
    
     ![] ]](rbrack.gif)              
    
            
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                |
| 99 | 98 | cbvralv 2577 |
. . . . . . 7
    
                        ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)              
        
            
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)               |
| 100 | 99 | rexbii 2373 |
. . . . . 6
        
                        ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)              
            
            
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)               |
| 101 | 91, 100 | sylib 120 |
. . . . 5
                      
                               
  ![] ]](rbrack.gif)                                            ![] ]](rbrack.gif)                                     
            
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)               |
| 102 | 101 | ex 113 |
. . . 4
                 
         
                      
     ![] ]](rbrack.gif)             
                           
  ![] ]](rbrack.gif)       
                                                ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                |
| 103 | 102 | ralrimiva 2434 |
. . 3
    
                                                  ![] ]](rbrack.gif)          
   
                       
     ![] ]](rbrack.gif)                                                       ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                |
| 104 | | oveq1 5539 |
. . . . . . . . . 10
        
     ![] ]](rbrack.gif)                    ![] ]](rbrack.gif)      |
| 105 | 104 | breq2d 3797 |
. . . . . . . . 9
        
     ![] ]](rbrack.gif)               
                 ![] ]](rbrack.gif)       |
| 106 | | breq1 3788 |
. . . . . . . . 9
        
     ![] ]](rbrack.gif)     
         
    
     ![] ]](rbrack.gif)              |
| 107 | 105, 106 | anbi12d 456 |
. . . . . . . 8
        
     ![] ]](rbrack.gif)                                          
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)               |
| 108 | 107 | imbi2d 228 |
. . . . . . 7
        
     ![] ]](rbrack.gif)                                   
    
            
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                |
| 109 | 108 | rexralbidv 2392 |
. . . . . 6
        
     ![] ]](rbrack.gif)                                           
            
            
     ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                |
| 110 | 109 | imbi2d 228 |
. . . . 5
        
     ![] ]](rbrack.gif)                                                                                      ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                 |
| 111 | 110 | ralbidv 2368 |
. . . 4
        
     ![] ]](rbrack.gif)         
    
                                        
   
    
                             ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                 |
| 112 | 111 | rspcev 2701 |
. . 3
             ![] ]](rbrack.gif)          
    
                             ![] ]](rbrack.gif)             
  ![] ]](rbrack.gif)                
                                                      |
| 113 | 10, 103, 112 | syl2anc 403 |
. 2
    
                                                  ![] ]](rbrack.gif)          
   
                       
     ![] ]](rbrack.gif)                                                                     |
| 114 | 8, 113 | rexlimddv 2481 |
1
                             
            
               |