Theorem issref 4727

Description: Two ways to state a relation is reflexive. Adapted from Tarski. (Contributed by FL, 15-Jan-2012.) (Revised by NM, 30-Mar-2016.)

Assertion

Ref	Expression
issref	|- ( ( _I |` A ) C_ R <-> A. x e. A x R x )

Distinct variable groups:   x, A   x, R

Proof of Theorem issref

Dummy variables y z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		df-ral 2353	. 2 |- ( A. x e. A x R x <-> A. x ( x e. A -> x R x ) )
2		vex 2604	. . . . 5 |- x e. _V
3		opelresi 4641	. . . . 5 |- ( x e. _V -> ( <. x , x >. e. ( _I |` A ) <-> x e. A ) )
4	2, 3	ax-mp 7	. . . 4 |- ( <. x , x >. e. ( _I |` A ) <-> x e. A )
5		df-br 3786	. . . . 5 |- ( x R x <-> <. x , x >. e. R )
6	5	bicomi 130	. . . 4 |- ( <. x , x >. e. R <-> x R x )
7	4, 6	imbi12i 237	. . 3 |- ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) <-> ( x e. A -> x R x ) )
8	7	albii 1399	. 2 |- ( A. x ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) <-> A. x ( x e. A -> x R x ) )
9		ralidm 3341	. . . . . 6 |- ( A. x e. _V A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) <-> A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) )
10		ralv 2616	. . . . . 6 |- ( A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) <-> A. x ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) )
11	9, 10	bitri 182	. . . . 5 |- ( A. x e. _V A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) <-> A. x ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) )
12		df-ral 2353	. . . . . . . . 9 |- ( A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) <-> A. x ( x e. _V -> ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) ) )
13		pm2.27 39	. . . . . . . . . . . 12 |- ( x e. _V -> ( ( x e. _V -> ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) ) -> ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) ) )
14		opelresg 4637	. . . . . . . . . . . . . . 15 |- ( z e. _V -> ( <. x , z >. e. ( _I |` A ) <-> ( <. x , z >. e. _I /\ x e. A ) ) )
15		df-br 3786	. . . . . . . . . . . . . . . . 17 |- ( x _I z <-> <. x , z >. e. _I )
16		vex 2604	. . . . . . . . . . . . . . . . . . 19 |- z e. _V
17	16	ideq 4506	. . . . . . . . . . . . . . . . . 18 |- ( x _I z <-> x = z )
18		opelresi 4641	. . . . . . . . . . . . . . . . . . . . 21 |- ( x e. A -> ( <. x , x >. e. ( _I |` A ) <-> x e. A ) )
19		pm2.27 39	. . . . . . . . . . . . . . . . . . . . . 22 |- ( <. x , x >. e. ( _I |` A ) -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> <. x , x >. e. R ) )
20		opeq2 3571	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( x = z -> <. x , x >. = <. x , z >. )
21	20	eleq1d 2147	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( x = z -> ( <. x , x >. e. R <-> <. x , z >. e. R ) )
22	21	biimpcd 157	. . . . . . . . . . . . . . . . . . . . . 22 |- ( <. x , x >. e. R -> ( x = z -> <. x , z >. e. R ) )
23	19, 22	syl6 33	. . . . . . . . . . . . . . . . . . . . 21 |- ( <. x , x >. e. ( _I |` A ) -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> ( x = z -> <. x , z >. e. R ) ) )
24	18, 23	syl6bir 162	. . . . . . . . . . . . . . . . . . . 20 |- ( x e. A -> ( x e. A -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> ( x = z -> <. x , z >. e. R ) ) ) )
25	24	pm2.43i 48	. . . . . . . . . . . . . . . . . . 19 |- ( x e. A -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> ( x = z -> <. x , z >. e. R ) ) )
26	25	com3r 78	. . . . . . . . . . . . . . . . . 18 |- ( x = z -> ( x e. A -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> <. x , z >. e. R ) ) )
27	17, 26	sylbi 119	. . . . . . . . . . . . . . . . 17 |- ( x _I z -> ( x e. A -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> <. x , z >. e. R ) ) )
28	15, 27	sylbir 133	. . . . . . . . . . . . . . . 16 |- ( <. x , z >. e. _I -> ( x e. A -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> <. x , z >. e. R ) ) )
29	28	imp 122	. . . . . . . . . . . . . . 15 |- ( ( <. x , z >. e. _I /\ x e. A ) -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> <. x , z >. e. R ) )
30	14, 29	syl6bi 161	. . . . . . . . . . . . . 14 |- ( z e. _V -> ( <. x , z >. e. ( _I |` A ) -> ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> <. x , z >. e. R ) ) )
31	30	com3r 78	. . . . . . . . . . . . 13 |- ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> ( z e. _V -> ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) ) )
32	31	ralrimiv 2433	. . . . . . . . . . . 12 |- ( ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> A. z e. _V ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) )
33	13, 32	syl6 33	. . . . . . . . . . 11 |- ( x e. _V -> ( ( x e. _V -> ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) ) -> A. z e. _V ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) ) )
34	2, 33	ax-mp 7	. . . . . . . . . 10 |- ( ( x e. _V -> ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) ) -> A. z e. _V ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) )
35	34	sps 1470	. . . . . . . . 9 |- ( A. x ( x e. _V -> ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) ) -> A. z e. _V ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) )
36	12, 35	sylbi 119	. . . . . . . 8 |- ( A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> A. z e. _V ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) )
37	36	ralimi 2426	. . . . . . 7 |- ( A. x e. _V A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> A. x e. _V A. z e. _V ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) )
38		eleq1 2141	. . . . . . . . 9 |- ( y = <. x , z >. -> ( y e. ( _I |` A ) <-> <. x , z >. e. ( _I |` A ) ) )
39		eleq1 2141	. . . . . . . . 9 |- ( y = <. x , z >. -> ( y e. R <-> <. x , z >. e. R ) )
40	38, 39	imbi12d 232	. . . . . . . 8 |- ( y = <. x , z >. -> ( ( y e. ( _I |` A ) -> y e. R ) <-> ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) ) )
41	40	ralxp 4497	. . . . . . 7 |- ( A. y e. ( _V X. _V ) ( y e. ( _I |` A ) -> y e. R ) <-> A. x e. _V A. z e. _V ( <. x , z >. e. ( _I |` A ) -> <. x , z >. e. R ) )
42	37, 41	sylibr 132	. . . . . 6 |- ( A. x e. _V A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> A. y e. ( _V X. _V ) ( y e. ( _I |` A ) -> y e. R ) )
43		df-ral 2353	. . . . . . 7 |- ( A. y e. ( _V X. _V ) ( y e. ( _I |` A ) -> y e. R ) <-> A. y ( y e. ( _V X. _V ) -> ( y e. ( _I |` A ) -> y e. R ) ) )
44		relres 4657	. . . . . . . . . . . 12 |- Rel ( _I |` A )
45		df-rel 4370	. . . . . . . . . . . 12 |- ( Rel ( _I |` A ) <-> ( _I |` A ) C_ ( _V X. _V ) )
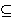46	44, 45	mpbi 143	. . . . . . . . . . 11 |- ( _I |` A ) C_ ( _V X. _V )
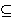47	46	sseli 2995	. . . . . . . . . 10 |- ( y e. ( _I |` A ) -> y e. ( _V X. _V ) )
48	47	ancri 317	. . . . . . . . 9 |- ( y e. ( _I |` A ) -> ( y e. ( _V X. _V ) /\ y e. ( _I |` A ) ) )
49		pm3.31 258	. . . . . . . . 9 |- ( ( y e. ( _V X. _V ) -> ( y e. ( _I |` A ) -> y e. R ) ) -> ( ( y e. ( _V X. _V ) /\ y e. ( _I |` A ) ) -> y e. R ) )
50	48, 49	syl5 32	. . . . . . . 8 |- ( ( y e. ( _V X. _V ) -> ( y e. ( _I |` A ) -> y e. R ) ) -> ( y e. ( _I |` A ) -> y e. R ) )
51	50	alimi 1384	. . . . . . 7 |- ( A. y ( y e. ( _V X. _V ) -> ( y e. ( _I |` A ) -> y e. R ) ) -> A. y ( y e. ( _I |` A ) -> y e. R ) )
52	43, 51	sylbi 119	. . . . . 6 |- ( A. y e. ( _V X. _V ) ( y e. ( _I |` A ) -> y e. R ) -> A. y ( y e. ( _I |` A ) -> y e. R ) )
53	42, 52	syl 14	. . . . 5 |- ( A. x e. _V A. x e. _V ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> A. y ( y e. ( _I |` A ) -> y e. R ) )
54	11, 53	sylbir 133	. . . 4 |- ( A. x ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> A. y ( y e. ( _I |` A ) -> y e. R ) )
55		dfss2 2988	. . . 4 |- ( ( _I |` A ) C_ R <-> A. y ( y e. ( _I |` A ) -> y e. R ) )
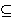56	54, 55	sylibr 132	. . 3 |- ( A. x ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) -> ( _I |` A ) C_ R )
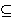57		ssel 2993	. . . 4 |- ( ( _I |` A ) C_ R -> ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) )
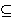
58	57	alrimiv 1795	. . 3 |- ( ( _I |` A ) C_ R -> A. x ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) )
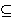
59	56, 58	impbii 124	. 2 |- ( A. x ( <. x , x >. e. ( _I |` A ) -> <. x , x >. e. R ) <-> ( _I |` A ) C_ R )
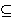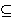60	1, 8, 59	3bitr2ri 207	1 |- ( ( _I |` A ) C_ R <-> A. x e. A x R x )

Syntax hints:   -> wi 4   /\ wa 102   <-> wb 103   A.wal 1282   = wceq 1284   e. wcel 1433   A.wral 2348   _Vcvv 2601   C_ wss 2973   <.cop 3401   class class class wbr 3785   _I cid 4043   X. cxp 4361   |` cres 4365   Rel wrel 4368

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-sep 3896  ax-pow 3948  ax-pr 3964

This theorem depends on definitions:  df-bi 115  df-3an 921  df-tru 1287  df-nf 1390  df-sb 1686  df-eu 1944  df-mo 1945  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ral 2353  df-rex 2354  df-v 2603  df-sbc 2816  df-csb 2909  df-un 2977  df-in 2979  df-ss 2986  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-iun 3680  df-br 3786  df-opab 3840  df-id 4048  df-xp 4369  df-rel 4370  df-res 4375

This theorem is referenced by: (None)