| Description: Axiom of Choice using
abbreviations. The logical equivalence to ax-ac 9281
can be established by chaining aceq0 8941 and aceq2 8942. A standard
textbook version of AC is derived from this one in dfac2a 8952, and this
version of AC is derived from the textbook version in dfac2 8953.
The following sketch will help you understand this version of the axiom.
Given any set  ,
the axiom says that there exists a ,
the axiom says that there exists a  that is a
collection of unordered pairs, one pair for each nonempty member of that is a
collection of unordered pairs, one pair for each nonempty member of
 . One entry in
the pair is the member of . One entry in
the pair is the member of  , and the other
entry is some arbitrary member of that member of , and the other
entry is some arbitrary member of that member of  . Using the
Axiom of Regularity, we can show that . Using the
Axiom of Regularity, we can show that  is really a set of ordered
pairs, very similar to the ordered pair construction opthreg 8515. The
key theorem for this (used in the proof of dfac2 8953) is preleq 8514. With
this modified definition of ordered pair, it can be seen that is really a set of ordered
pairs, very similar to the ordered pair construction opthreg 8515. The
key theorem for this (used in the proof of dfac2 8953) is preleq 8514. With
this modified definition of ordered pair, it can be seen that  is
actually a choice function on the members of is
actually a choice function on the members of  . .
For example, suppose             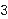      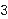  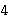   .
Let us try .
Let us try                  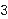     
    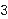  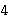      . For the member (of . For the member (of  ) )
       , the only assignment to , the only assignment to  and and  that
satisfies the axiom is that
satisfies the axiom is    and and            , so
there is exactly one , so
there is exactly one  as required. We verify the other two members
of as required. We verify the other two members
of  similarly.
Thus, similarly.
Thus,  satisfies the
axiom. Using our
modified ordered pair definition, we can say that satisfies the
axiom. Using our
modified ordered pair definition, we can say that  corresponds to
the choice function corresponds to
the choice function  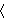        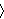 
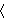    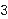    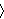 
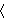    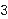  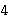    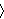  . Of course other choices for . Of course other choices for  will
also satisfy the axiom, for example will
also satisfy the axiom, for example
                 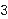     
    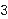  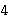   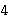   . What AC tells us is that there exists at
least one such . What AC tells us is that there exists at
least one such  ,
but it doesn't tell us which one. ,
but it doesn't tell us which one.
(New usage is discouraged.) (Contributed by NM,
19-Jul-1996.) |