Theorem prarloclem5 6690

Description: A substitution of zero for y and N minus two for x. Lemma for prarloc 6693. (Contributed by Jim Kingdon, 4-Nov-2019.)

Assertion

Ref	Expression
prarloclem5	|- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> E. x e. om E. y e. om ( ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) )

Distinct variable groups:   x, A, y   x, L, y   x, N   x, P, y   x, U, y

Allowed substitution hint:   N( y)

Proof of Theorem prarloclem5

Step	Hyp	Ref	Expression
1		prarloclemn 6689	. . . 4 |- ( ( N e. N. /\ 1o <N N ) -> E. x e. om ( 2o +o x ) = N )
2	1	3adant2 957	. . 3 |- ( ( N e. N. /\ P e. Q. /\ 1o <N N ) -> E. x e. om ( 2o +o x ) = N )
3	2	3ad2ant2 960	. 2 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> E. x e. om ( 2o +o x ) = N )
4		elprnql 6671	. . . . . . 7 |- ( ( <. L , U >. e. P. /\ A e. L ) -> A e. Q. )
5	4	3ad2ant1 959	. . . . . 6 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> A e. Q. )
6		simp22 972	. . . . . 6 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> P e. Q. )
7		nqnq0 6631	. . . . . . . . 9 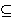|- Q. C_ Q0
8	7	sseli 2995	. . . . . . . 8 |- ( A e. Q. -> A e. Q0 )
9		nq0a0 6647	. . . . . . . 8 |- ( A e. Q0 -> ( A +Q0 0Q0 ) = A )
10	8, 9	syl 14	. . . . . . 7 |- ( A e. Q. -> ( A +Q0 0Q0 ) = A )
11		df-0nq0 6616	. . . . . . . . . 10 |- 0Q0 = [ <. (/) , 1o >. ] ~Q0
12	11	oveq1i 5542	. . . . . . . . 9 |- (0Q0 ·Q0 P ) = ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P )
13	7	sseli 2995	. . . . . . . . . 10 |- ( P e. Q. -> P e. Q0 )
14		nq0m0r 6646	. . . . . . . . . 10 |- ( P e. Q0 -> (0Q0 ·Q0 P ) = 0Q0 )
15	13, 14	syl 14	. . . . . . . . 9 |- ( P e. Q. -> (0Q0 ·Q0 P ) = 0Q0 )
16	12, 15	syl5reqr 2128	. . . . . . . 8 |- ( P e. Q. -> 0Q0 = ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) )
17	16	oveq2d 5548	. . . . . . 7 |- ( P e. Q. -> ( A +Q0 0Q0 ) = ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) )
18	10, 17	sylan9req 2134	. . . . . 6 |- ( ( A e. Q. /\ P e. Q. ) -> A = ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) )
19	5, 6, 18	syl2anc 403	. . . . 5 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> A = ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) )
20		simp1r 963	. . . . 5 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> A e. L )
21	19, 20	eqeltrrd 2156	. . . 4 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) e. L )
22		2onn 6117	. . . . . . . . . . . . . . 15 |- 2o e. om
23		nna0r 6080	. . . . . . . . . . . . . . 15 |- ( 2o e. om -> ( (/) +o 2o ) = 2o )
24	22, 23	ax-mp 7	. . . . . . . . . . . . . 14 |- ( (/) +o 2o ) = 2o
25	24	oveq1i 5542	. . . . . . . . . . . . 13 |- ( ( (/) +o 2o ) +o x ) = ( 2o +o x )
26	25	eqeq1i 2088	. . . . . . . . . . . 12 |- ( ( ( (/) +o 2o ) +o x ) = N <-> ( 2o +o x ) = N )
27	26	biimpri 131	. . . . . . . . . . 11 |- ( ( 2o +o x ) = N -> ( ( (/) +o 2o ) +o x ) = N )
28	27	opeq1d 3576	. . . . . . . . . 10 |- ( ( 2o +o x ) = N -> <. ( ( (/) +o 2o ) +o x ) , 1o >. = <. N , 1o >. )
29	28	eceq1d 6165	. . . . . . . . 9 |- ( ( 2o +o x ) = N -> [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q = [ <. N , 1o >. ] ~Q )
30	29	oveq1d 5547	. . . . . . . 8 |- ( ( 2o +o x ) = N -> ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) = ( [ <. N , 1o >. ] ~Q .Q P ) )
31	30	oveq2d 5548	. . . . . . 7 |- ( ( 2o +o x ) = N -> ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) = ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) )
32	31	eleq1d 2147	. . . . . 6 |- ( ( 2o +o x ) = N -> ( ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U <-> ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) )
33	32	biimprcd 158	. . . . 5 |- ( ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U -> ( ( 2o +o x ) = N -> ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) )
34	33	3ad2ant3 961	. . . 4 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> ( ( 2o +o x ) = N -> ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) )
35		peano1 4335	. . . . 5 |- (/) e. om
36		opeq1 3570	. . . . . . . . . . 11 |- ( y = (/) -> <. y , 1o >. = <. (/) , 1o >. )
37	36	eceq1d 6165	. . . . . . . . . 10 |- ( y = (/) -> [ <. y , 1o >. ] ~Q0 = [ <. (/) , 1o >. ] ~Q0 )
38	37	oveq1d 5547	. . . . . . . . 9 |- ( y = (/) -> ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) = ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) )
39	38	oveq2d 5548	. . . . . . . 8 |- ( y = (/) -> ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) = ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) )
40	39	eleq1d 2147	. . . . . . 7 |- ( y = (/) -> ( ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) e. L <-> ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) e. L ) )
41		oveq1 5539	. . . . . . . . . . . . 13 |- ( y = (/) -> ( y +o 2o ) = ( (/) +o 2o ) )
42	41	oveq1d 5547	. . . . . . . . . . . 12 |- ( y = (/) -> ( ( y +o 2o ) +o x ) = ( ( (/) +o 2o ) +o x ) )
43	42	opeq1d 3576	. . . . . . . . . . 11 |- ( y = (/) -> <. ( ( y +o 2o ) +o x ) , 1o >. = <. ( ( (/) +o 2o ) +o x ) , 1o >. )
44	43	eceq1d 6165	. . . . . . . . . 10 |- ( y = (/) -> [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q = [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q )
45	44	oveq1d 5547	. . . . . . . . 9 |- ( y = (/) -> ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) = ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) )
46	45	oveq2d 5548	. . . . . . . 8 |- ( y = (/) -> ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) = ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) )
47	46	eleq1d 2147	. . . . . . 7 |- ( y = (/) -> ( ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U <-> ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) )
48	40, 47	anbi12d 456	. . . . . 6 |- ( y = (/) -> ( ( ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) <-> ( ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) ) )
49	48	rspcev 2701	. . . . 5 |- ( ( (/) e. om /\ ( ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) ) -> E. y e. om ( ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) )
50	35, 49	mpan 414	. . . 4 |- ( ( ( A +Q0 ( [ <. (/) , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( (/) +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) -> E. y e. om ( ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) )
51	21, 34, 50	syl6an 1363	. . 3 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> ( ( 2o +o x ) = N -> E. y e. om ( ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) ) )
52	51	reximdv 2462	. 2 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> ( E. x e. om ( 2o +o x ) = N -> E. x e. om E. y e. om ( ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) ) )
53	3, 52	mpd 13	1 |- ( ( ( <. L , U >. e. P. /\ A e. L ) /\ ( N e. N. /\ P e. Q. /\ 1o <N N ) /\ ( A +Q ( [ <. N , 1o >. ] ~Q .Q P ) ) e. U ) -> E. x e. om E. y e. om ( ( A +Q0 ( [ <. y , 1o >. ] ~Q0 ·Q0 P ) ) e. L /\ ( A +Q ( [ <. ( ( y +o 2o ) +o x ) , 1o >. ] ~Q .Q P ) ) e. U ) )

Syntax hints:   -> wi 4   /\ wa 102   /\ w3a 919   = wceq 1284   e. wcel 1433   E.wrex 2349   (/)c0 3251   <.cop 3401   class class class wbr 3785   omcom 4331  (class class class)co 5532   1oc1o 6017   2oc2o 6018   +o coa 6021   [cec 6127   N.cnpi 6462   <N clti 6465   ~Q ceq 6469   Q.cnq 6470   +Q cplq 6472   .Q cmq 6473   ~_Q0 ceq0 6476  Q₀cnq0 6477  0_Q0c0q0 6478   +_Q0 cplq0 6479   ·_Q0 cmq0 6480   P.cnp 6481

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-in1 576  ax-in2 577  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-13 1444  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-coll 3893  ax-sep 3896  ax-nul 3904  ax-pow 3948  ax-pr 3964  ax-un 4188  ax-setind 4280  ax-iinf 4329

This theorem depends on definitions:  df-bi 115  df-dc 776  df-3or 920  df-3an 921  df-tru 1287  df-fal 1290  df-nf 1390  df-sb 1686  df-eu 1944  df-mo 1945  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ne 2246  df-ral 2353  df-rex 2354  df-reu 2355  df-rab 2357  df-v 2603  df-sbc 2816  df-csb 2909  df-dif 2975  df-un 2977  df-in 2979  df-ss 2986  df-nul 3252  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-uni 3602  df-int 3637  df-iun 3680  df-br 3786  df-opab 3840  df-mpt 3841  df-tr 3876  df-eprel 4044  df-id 4048  df-iord 4121  df-on 4123  df-suc 4126  df-iom 4332  df-xp 4369  df-rel 4370  df-cnv 4371  df-co 4372  df-dm 4373  df-rn 4374  df-res 4375  df-ima 4376  df-iota 4887  df-fun 4924  df-fn 4925  df-f 4926  df-f1 4927  df-fo 4928  df-f1o 4929  df-fv 4930  df-ov 5535  df-oprab 5536  df-mpt2 5537  df-1st 5787  df-2nd 5788  df-recs 5943  df-irdg 5980  df-1o 6024  df-2o 6025  df-oadd 6028  df-omul 6029  df-er 6129  df-ec 6131  df-qs 6135  df-ni 6494  df-mi 6496  df-lti 6497  df-enq 6537  df-nqqs 6538  df-enq0 6614  df-nq0 6615  df-0nq0 6616  df-plq0 6617  df-mq0 6618  df-inp 6656

This theorem is referenced by:  prarloclem  6691