Users' Mathboxes Mathbox for Norm Megill < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  MPE Home  >  Th. List  >   Mathboxes  >  cdleme32fva Structured version   Visualization version   Unicode version
Theorem cdleme32fva 35725
Description: Part of proof of Lemma D in [Crawley] p. 113. Value of F at an atom not under W. (Contributed by NM, 2-Mar-2013.)
Hypotheses
Ref Expression
cdleme32.b |- B = ( Base ` K )
cdleme32.l |- .<_ = ( le ` K )
cdleme32.j |- .\/ = ( join ` K )
cdleme32.m |- ./\ = ( meet ` K )
cdleme32.a |- A = ( Atoms ` K )
cdleme32.h |- H = ( LHyp ` K )
cdleme32.u |- U = ( ( P .\/ Q ) ./\ W )
cdleme32.c |- C = ( ( s .\/ U ) ./\ ( Q .\/ ( ( P .\/ s ) ./\ W ) ) )
cdleme32.d |- D = ( ( t .\/ U ) ./\ ( Q .\/ ( ( P .\/ t ) ./\ W ) ) )
cdleme32.e |- E = ( ( P .\/ Q ) ./\ ( D .\/ ( ( s .\/ t ) ./\ W ) ) )
cdleme32.i |- I = ( iota_ y e. B A. t e. A ( ( -. t .<_ W /\ -. t .<_ ( P .\/ Q ) ) -> y = E ) )
cdleme32.n |- N = if ( s .<_ ( P .\/ Q ) , I , C )
cdleme32.o |- O = ( iota_ z e. B A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( x ./\ W ) ) = x ) -> z = ( N .\/ ( x ./\ W ) ) ) )
cdleme32.f |- F = ( x e. B |-> if ( ( P =/= Q /\ -. x .<_ W ) , O , x ) )
Assertion
Ref Expression
cdleme32fva |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> [_ R / x ]_ O = [_ R / s ]_ N )
Distinct variable groups:   t, s, x, y, z, A   B, s, t, x, y, z   y, C   D, s, y, z   y, E   H, s, t   .\/ , s, t, x, y, z   K, s, t   .<_ , s, t, x, y, z   ./\ , s, t, x, y, z   x, N, z   P, s, t, x, y, z   Q, s, t, x, y, z   U, s, t, x, y, z   W, s, t, x, y, z   R, s, t, y   y, H   y, K   x, R, z   z, H   z, K
Allowed substitution hints:   C( x, z, t, s)   D( x, t)   E( x, z, t, s)   F( x, y, z, t, s)   H( x)   I( x, y, z, t, s)   K( x)   N( y, t, s)   O( x, y, z, t, s)
Proof of Theorem cdleme32fva
StepHypRef Expression
1 simp2l 1087 . . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> R e. A )
2 cdleme32.b . . . . 5 |- B = ( Base ` K )
3 cdleme32.a . . . . 5 |- A = ( Atoms ` K )
42, 3atbase 34576 . . . 4 |- ( R e. A -> R e. B )
51, 4syl 17 . . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> R e. B )
6 cdleme32.o . . . 4 |- O = ( iota_ z e. B A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( x ./\ W ) ) = x ) -> z = ( N .\/ ( x ./\ W ) ) ) )
7 eqid 2622 . . . 4 |- ( iota_ z e. B A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) = ( iota_ z e. B A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) )
86, 7cdleme31so 35667 . . 3 |- ( R e. B -> [_ R / x ]_ O = ( iota_ z e. B A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) )
95, 8syl 17 . 2 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> [_ R / x ]_ O = ( iota_ z e. B A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) )
10 simp1 1061 . . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) )
11 simp3 1063 . . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> P =/= Q )
12 simp2 1062 . . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( R e. A /\ -. R .<_ W ) )
13 cdleme32.l . . . . 5 |- .<_ = ( le ` K )
14 cdleme32.j . . . . 5 |- .\/ = ( join ` K )
15 cdleme32.m . . . . 5 |- ./\ = ( meet ` K )
16 cdleme32.h . . . . 5 |- H = ( LHyp ` K )
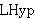17 cdleme32.u . . . . 5 |- U = ( ( P .\/ Q ) ./\ W )
18 cdleme32.c . . . . 5 |- C = ( ( s .\/ U ) ./\ ( Q .\/ ( ( P .\/ s ) ./\ W ) ) )
19 cdleme32.d . . . . 5 |- D = ( ( t .\/ U ) ./\ ( Q .\/ ( ( P .\/ t ) ./\ W ) ) )
20 cdleme32.e . . . . 5 |- E = ( ( P .\/ Q ) ./\ ( D .\/ ( ( s .\/ t ) ./\ W ) ) )
21 cdleme32.i . . . . 5 |- I = ( iota_ y e. B A. t e. A ( ( -. t .<_ W /\ -. t .<_ ( P .\/ Q ) ) -> y = E ) )
22 cdleme32.n . . . . 5 |- N = if ( s .<_ ( P .\/ Q ) , I , C )
232, 13, 14, 15, 3, 16, 17, 18, 19, 20, 21, 22cdleme32snb 35724 . . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) ) -> [_ R / s ]_ N e. B )
2410, 11, 12, 23syl12anc 1324 . . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> [_ R / s ]_ N e. B )
25 nfv 1843 . . . . . . . . 9 |- F/ s -. R .<_ W
26 nfcsb1v 3549 . . . . . . . . . 10 |- F/_ s [_ R / s ]_ N
2726nfeq2 2780 . . . . . . . . 9 |- F/ s z = [_ R / s ]_ N
2825, 27nfim 1825 . . . . . . . 8 |- F/ s ( -. R .<_ W -> z = [_ R / s ]_ N )
29 breq1 4656 . . . . . . . . . . 11 |- ( s = R -> ( s .<_ W <-> R .<_ W ) )
3029notbid 308 . . . . . . . . . 10 |- ( s = R -> ( -. s .<_ W <-> -. R .<_ W ) )
31 csbeq1a 3542 . . . . . . . . . . 11 |- ( s = R -> N = [_ R / s ]_ N )
3231eqeq2d 2632 . . . . . . . . . 10 |- ( s = R -> ( z = N <-> z = [_ R / s ]_ N ) )
3330, 32imbi12d 334 . . . . . . . . 9 |- ( s = R -> ( ( -. s .<_ W -> z = N ) <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) )
3433ax-gen 1722 . . . . . . . 8 |- A. s ( s = R -> ( ( -. s .<_ W -> z = N ) <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) )
35 ceqsralt 3229 . . . . . . . 8 |- ( ( F/ s ( -. R .<_ W -> z = [_ R / s ]_ N ) /\ A. s ( s = R -> ( ( -. s .<_ W -> z = N ) <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) ) /\ R e. A ) -> ( A. s e. A ( s = R -> ( -. s .<_ W -> z = N ) ) <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) )
3628, 34, 35mp3an12 1414 . . . . . . 7 |- ( R e. A -> ( A. s e. A ( s = R -> ( -. s .<_ W -> z = N ) ) <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) )
3736adantr 481 . . . . . 6 |- ( ( R e. A /\ -. R .<_ W ) -> ( A. s e. A ( s = R -> ( -. s .<_ W -> z = N ) ) <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) )
38373ad2ant2 1083 . . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( A. s e. A ( s = R -> ( -. s .<_ W -> z = N ) ) <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) )
39 simp11 1091 . . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( K e. HL /\ W e. H ) )
40 eqid 2622 . . . . . . . . . . . . . . . 16 |- ( 0. ` K ) = ( 0. ` K )
4113, 15, 40, 3, 16lhpmat 35316 . . . . . . . . . . . . . . 15 |- ( ( ( K e. HL /\ W e. H ) /\ ( R e. A /\ -. R .<_ W ) ) -> ( R ./\ W ) = ( 0. ` K ) )
4239, 12, 41syl2anc 693 . . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( R ./\ W ) = ( 0. ` K ) )
4342adantr 481 . . . . . . . . . . . . 13 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( R ./\ W ) = ( 0. ` K ) )
4443oveq2d 6666 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( s .\/ ( R ./\ W ) ) = ( s .\/ ( 0. ` K ) ) )
45 simp11l 1172 . . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> K e. HL )
4645adantr 481 . . . . . . . . . . . . . 14 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> K e. HL )
47 hlol 34648 . . . . . . . . . . . . . 14 |- ( K e. HL -> K e. OL )
4846, 47syl 17 . . . . . . . . . . . . 13 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> K e. OL )
492, 3atbase 34576 . . . . . . . . . . . . . 14 |- ( s e. A -> s e. B )
5049ad2antrl 764 . . . . . . . . . . . . 13 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> s e. B )
512, 14, 40olj01 34512 . . . . . . . . . . . . 13 |- ( ( K e. OL /\ s e. B ) -> ( s .\/ ( 0. ` K ) ) = s )
5248, 50, 51syl2anc 693 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( s .\/ ( 0. ` K ) ) = s )
5344, 52eqtrd 2656 . . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( s .\/ ( R ./\ W ) ) = s )
5453eqeq1d 2624 . . . . . . . . . 10 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( ( s .\/ ( R ./\ W ) ) = R <-> s = R ) )
5543oveq2d 6666 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( N .\/ ( R ./\ W ) ) = ( N .\/ ( 0. ` K ) ) )
56 simpl11 1136 . . . . . . . . . . . . . 14 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( K e. HL /\ W e. H ) )
57 simpl12 1137 . . . . . . . . . . . . . 14 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( P e. A /\ -. P .<_ W ) )
58 simpl13 1138 . . . . . . . . . . . . . 14 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( Q e. A /\ -. Q .<_ W ) )
59 simpr 477 . . . . . . . . . . . . . 14 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( s e. A /\ -. s .<_ W ) )
60 simpl3 1066 . . . . . . . . . . . . . 14 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> P =/= Q )
612, 13, 14, 15, 3, 16, 17, 18, 19, 20, 21, 22cdleme27cl 35654 . . . . . . . . . . . . . 14 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( ( s e. A /\ -. s .<_ W ) /\ P =/= Q ) ) -> N e. B )
6256, 57, 58, 59, 60, 61syl122anc 1335 . . . . . . . . . . . . 13 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> N e. B )
632, 14, 40olj01 34512 . . . . . . . . . . . . 13 |- ( ( K e. OL /\ N e. B ) -> ( N .\/ ( 0. ` K ) ) = N )
6448, 62, 63syl2anc 693 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( N .\/ ( 0. ` K ) ) = N )
6555, 64eqtrd 2656 . . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( N .\/ ( R ./\ W ) ) = N )
6665eqeq2d 2632 . . . . . . . . . 10 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( z = ( N .\/ ( R ./\ W ) ) <-> z = N ) )
6754, 66imbi12d 334 . . . . . . . . 9 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ ( s e. A /\ -. s .<_ W ) ) -> ( ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) <-> ( s = R -> z = N ) ) )
6867expr 643 . . . . . . . 8 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ s e. A ) -> ( -. s .<_ W -> ( ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) <-> ( s = R -> z = N ) ) ) )
6968pm5.74d 262 . . . . . . 7 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ s e. A ) -> ( ( -. s .<_ W -> ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) ) <-> ( -. s .<_ W -> ( s = R -> z = N ) ) ) )
70 impexp 462 . . . . . . 7 |- ( ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> ( -. s .<_ W -> ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) ) )
71 bi2.04 376 . . . . . . 7 |- ( ( s = R -> ( -. s .<_ W -> z = N ) ) <-> ( -. s .<_ W -> ( s = R -> z = N ) ) )
7269, 70, 713bitr4g 303 . . . . . 6 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ s e. A ) -> ( ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> ( s = R -> ( -. s .<_ W -> z = N ) ) ) )
7372ralbidva 2985 . . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> A. s e. A ( s = R -> ( -. s .<_ W -> z = N ) ) ) )
74 simp2r 1088 . . . . . 6 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> -. R .<_ W )
75 biimt 350 . . . . . 6 |- ( -. R .<_ W -> ( z = [_ R / s ]_ N <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) )
7674, 75syl 17 . . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( z = [_ R / s ]_ N <-> ( -. R .<_ W -> z = [_ R / s ]_ N ) ) )
7738, 73, 763bitr4d 300 . . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> z = [_ R / s ]_ N ) )
7877adantr 481 . . 3 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) /\ z e. B ) -> ( A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> z = [_ R / s ]_ N ) )
7924, 78riota5 6637 . 2 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> ( iota_ z e. B A. s e. A ( ( -. s .<_ W /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) = [_ R / s ]_ N )
809, 79eqtrd 2656 1 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( R e. A /\ -. R .<_ W ) /\ P =/= Q ) -> [_ R / x ]_ O = [_ R / s ]_ N )
Colors of variables: wff setvar class
Syntax hints:   -. wn 3   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   A.wal 1481   = wceq 1483   F/wnf 1708   e. wcel 1990   =/= wne 2794   A.wral 2912   [_csb 3533   ifcif 4086   class class class wbr 4653   |-> cmpt 4729   ` cfv 5888   iota_crio 6610  (class class class)co 6650   Basecbs 15857   lecple 15948   joincjn 16944   meetcmee 16945   0.cp0 17037   OLcol 34461   Atomscatm 34550   HLchlt 34637   LHypclh 35270
This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-riotaBAD 34239
This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-1st 7168  df-2nd 7169  df-undef 7399  df-preset 16928  df-poset 16946  df-plt 16958  df-lub 16974  df-glb 16975  df-join 16976  df-meet 16977  df-p0 17039  df-p1 17040  df-lat 17046  df-clat 17108  df-oposet 34463  df-ol 34465  df-oml 34466  df-covers 34553  df-ats 34554  df-atl 34585  df-cvlat 34609  df-hlat 34638  df-llines 34784  df-lplanes 34785  df-lvols 34786  df-lines 34787  df-psubsp 34789  df-pmap 34790  df-padd 35082  df-lhyp 35274
This theorem is referenced by:  cdleme32fva1  35726
  Copyright terms: Public domain W3C validator