Theorem cdlemk34 36198

Description: Part of proof of Lemma K of [Crawley] p. 118. TODO: fix comment. Part of attempt to simplify hypotheses. (Contributed by NM, 18-Jul-2013.)

Hypotheses

Ref	Expression
cdlemk3.b	|- B = ( Base ` K )
cdlemk3.l	|- .<_ = ( le ` K )
cdlemk3.j	|- .\/ = ( join ` K )
cdlemk3.m	|- ./\ = ( meet ` K )
cdlemk3.a	|- A = ( Atoms ` K )
cdlemk3.h	|- H = ( LHyp ` K )
cdlemk3.t	|- T = ( ( LTrn ` K ) ` W )
cdlemk3.r	|- R = ( ( trL ` K ) ` W )
cdlemk3.s	|- S = ( f e. T |-> ( iota_ i e. T ( i ` P ) = ( ( P .\/ ( R ` f ) ) ./\ ( ( N ` P ) .\/ ( R ` ( f o. `' F ) ) ) ) ) )
cdlemk3.u1	|- Y = ( d e. T , e e. T |-> ( iota_ j e. T ( j ` P ) = ( ( P .\/ ( R ` e ) ) ./\ ( ( ( S ` d ) ` P ) .\/ ( R ` ( e o. `' d ) ) ) ) ) )
cdlemk3.x	|- X = ( iota_ z e. T A. b e. T ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> z = ( b Y G ) ) )

Assertion

Ref

Expression

cdlemk34

|- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> X = ( iota_ z e. T A. b e. T ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) ) )

Distinct variable groups:   e, d, f, i, ./\   .<_ , i   .\/ , d, e, f, i   A, i   j, d, e, f, i, F   G, d, e, j   i, H   i, K   f, N, i   P, d, e, f, i   R, d, e, f, i   T, d, e, f, i   W, d, e, f, i, b   ./\ , j   .<_ , j   .\/ , j   A, j   j, F   j, H   j, K   j, N   P, j   R, j   b, d, S, e, j   T, j   j, W   F, d, e   .<_ , e   f, G, i   .<_ , b   A, b, z   B, b, z   F, b, z   G, b, z   H, b   K, b   N, b   P, b   R, b, z   T, b, z   W, b, z   Y, b, z   z, d, e, f, i, j   z, .<_   z, A   z, H   z, K   z, N   z, P

Allowed substitution hints:   A( e, f, d)   B( e, f, i, j, d)   S( z, f, i)   H( e, f, d)   .\/ ( z, b)   K( e, f, d)   .<_ ( f, d)   ./\ ( z, b)   N( e, d)   X( z, e, f, i, j, b, d)   Y( e, f, i, j, d)

Proof of Theorem cdlemk34

Step	Hyp	Ref	Expression
1		cdlemk3.x	. 2 |- X = ( iota_ z e. T A. b e. T ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> z = ( b Y G ) ) )
2		fveq1 6190	. . . . . . . . 9 |- ( z = ( b Y G ) -> ( z ` P ) = ( ( b Y G ) ` P ) )
3		simpll1 1100	. . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> ( K e. HL /\ W e. H ) )
4		simplr1 1103	. . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> z e. T )
5		simpl1 1064	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( K e. HL /\ W e. H ) )
6		simpl3r 1117	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( R ` F ) = ( R ` N ) )
7		simp22l 1180	. . . . . . . . . . . . . . 15 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> G e. T )
8	7	adantr 481	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> G e. T )
9	5, 6, 8	3jca 1242	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( ( K e. HL /\ W e. H ) /\ ( R ` F ) = ( R ` N ) /\ G e. T ) )
10	9	adantr 481	. . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> ( ( K e. HL /\ W e. H ) /\ ( R ` F ) = ( R ` N ) /\ G e. T ) )
11		simp21l 1178	. . . . . . . . . . . . . . 15 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> F e. T )
12	11	adantr 481	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> F e. T )
13		simpr2 1068	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> b e. T )
14		simpl23 1141	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> N e. T )
15	12, 13, 14	3jca 1242	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( F e. T /\ b e. T /\ N e. T ) )
16	15	adantr 481	. . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> ( F e. T /\ b e. T /\ N e. T ) )
17		simpr32 1152	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( R ` b ) =/= ( R ` F ) )
18		simpr33 1153	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( R ` b ) =/= ( R ` G ) )
19	17, 18	jca 554	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) )
20	19	adantr 481	. . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> ( ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) )
21		simp21r 1179	. . . . . . . . . . . . . . 15 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> F =/= ( _I |` B ) )
22	21	adantr 481	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> F =/= ( _I |` B ) )
23		simp22r 1181	. . . . . . . . . . . . . . 15 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> G =/= ( _I |` B ) )
24	23	adantr 481	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> G =/= ( _I |` B ) )
25		simpr31 1151	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> b =/= ( _I |` B ) )
26	22, 24, 25	3jca 1242	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( F =/= ( _I |` B ) /\ G =/= ( _I |` B ) /\ b =/= ( _I |` B ) ) )
27	26	adantr 481	. . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> ( F =/= ( _I |` B ) /\ G =/= ( _I |` B ) /\ b =/= ( _I |` B ) ) )
28		simpl3l 1116	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( P e. A /\ -. P .<_ W ) )
29	28	adantr 481	. . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> ( P e. A /\ -. P .<_ W ) )
30		cdlemk3.b	. . . . . . . . . . . . 13 |- B = ( Base ` K )
31		cdlemk3.l	. . . . . . . . . . . . 13 |- .<_ = ( le ` K )
32		cdlemk3.j	. . . . . . . . . . . . 13 |- .\/ = ( join ` K )
33		cdlemk3.m	. . . . . . . . . . . . 13 |- ./\ = ( meet ` K )
34		cdlemk3.a	. . . . . . . . . . . . 13 |- A = ( Atoms ` K )
35		cdlemk3.h	. . . . . . . . . . . . 13 |- H = ( LHyp ` K )
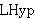36		cdlemk3.t	. . . . . . . . . . . . 13 |- T = ( ( LTrn ` K ) ` W )
37		cdlemk3.r	. . . . . . . . . . . . 13 |- R = ( ( trL ` K ) ` W )
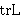38		cdlemk3.s	. . . . . . . . . . . . 13 |- S = ( f e. T |-> ( iota_ i e. T ( i ` P ) = ( ( P .\/ ( R ` f ) ) ./\ ( ( N ` P ) .\/ ( R ` ( f o. `' F ) ) ) ) ) )
39		cdlemk3.u1	. . . . . . . . . . . . 13 |- Y = ( d e. T , e e. T |-> ( iota_ j e. T ( j ` P ) = ( ( P .\/ ( R ` e ) ) ./\ ( ( ( S ` d ) ` P ) .\/ ( R ` ( e o. `' d ) ) ) ) ) )
40	30, 31, 32, 33, 34, 35, 36, 37, 38, 39	cdlemkuel-3 36186	. . . . . . . . . . . 12 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( R ` F ) = ( R ` N ) /\ G e. T ) /\ ( F e. T /\ b e. T /\ N e. T ) /\ ( ( ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) /\ ( F =/= ( _I |` B ) /\ G =/= ( _I |` B ) /\ b =/= ( _I |` B ) ) /\ ( P e. A /\ -. P .<_ W ) ) ) -> ( b Y G ) e. T )
41	10, 16, 20, 27, 29, 40	syl113anc 1338	. . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> ( b Y G ) e. T )
42		simpr 477	. . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> ( z ` P ) = ( ( b Y G ) ` P ) )
43	31, 34, 35, 36	cdlemd 35494	. . . . . . . . . . 11 |- ( ( ( ( K e. HL /\ W e. H ) /\ z e. T /\ ( b Y G ) e. T ) /\ ( P e. A /\ -. P .<_ W ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> z = ( b Y G ) )
44	3, 4, 41, 29, 42, 43	syl311anc 1340	. . . . . . . . . 10 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) /\ ( z ` P ) = ( ( b Y G ) ` P ) ) -> z = ( b Y G ) )
45	44	ex 450	. . . . . . . . 9 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( ( z ` P ) = ( ( b Y G ) ` P ) -> z = ( b Y G ) ) )
46	2, 45	impbid2 216	. . . . . . . 8 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( z = ( b Y G ) <-> ( z ` P ) = ( ( b Y G ) ` P ) ) )
47		simp1 1061	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> ( K e. HL /\ W e. H ) )
48		simp3r 1090	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> ( R ` F ) = ( R ` N ) )
49	47, 48	jca 554	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> ( ( K e. HL /\ W e. H ) /\ ( R ` F ) = ( R ` N ) ) )
50	49	adantr 481	. . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( ( K e. HL /\ W e. H ) /\ ( R ` F ) = ( R ` N ) ) )
51	22, 25, 24	3jca 1242	. . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( F =/= ( _I |` B ) /\ b =/= ( _I |` B ) /\ G =/= ( _I |` B ) ) )
52	30, 31, 32, 33, 34, 35, 36, 37, 38, 39	cdlemk32 36185	. . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( R ` F ) = ( R ` N ) ) /\ ( ( F e. T /\ b e. T /\ N e. T ) /\ G e. T ) /\ ( ( ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) /\ ( F =/= ( _I |` B ) /\ b =/= ( _I |` B ) /\ G =/= ( _I |` B ) ) /\ ( P e. A /\ -. P .<_ W ) ) ) -> ( ( b Y G ) ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) )
53	50, 15, 8, 19, 51, 28, 52	syl123anc 1343	. . . . . . . . 9 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( ( b Y G ) ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) )
54	53	eqeq2d 2632	. . . . . . . 8 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( ( z ` P ) = ( ( b Y G ) ` P ) <-> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) )
55	46, 54	bitrd 268	. . . . . . 7 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ ( z e. T /\ b e. T /\ ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) ) ) -> ( z = ( b Y G ) <-> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) )
56	55	3exp2 1285	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> ( z e. T -> ( b e. T -> ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> ( z = ( b Y G ) <-> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) ) ) ) )
57	56	imp31 448	. . . . 5 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ z e. T ) /\ b e. T ) -> ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> ( z = ( b Y G ) <-> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) ) )
58	57	pm5.74d 262	. . . 4 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ z e. T ) /\ b e. T ) -> ( ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> z = ( b Y G ) ) <-> ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) ) )
59	58	ralbidva 2985	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) /\ z e. T ) -> ( A. b e. T ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> z = ( b Y G ) ) <-> A. b e. T ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) ) )
60	59	riotabidva 6627	. 2 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> ( iota_ z e. T A. b e. T ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> z = ( b Y G ) ) ) = ( iota_ z e. T A. b e. T ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) ) )
61	1, 60	syl5eq 2668	1 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( F e. T /\ F =/= ( _I |` B ) ) /\ ( G e. T /\ G =/= ( _I |` B ) ) /\ N e. T ) /\ ( ( P e. A /\ -. P .<_ W ) /\ ( R ` F ) = ( R ` N ) ) ) -> X = ( iota_ z e. T A. b e. T ( ( b =/= ( _I |` B ) /\ ( R ` b ) =/= ( R ` F ) /\ ( R ` b ) =/= ( R ` G ) ) -> ( z ` P ) = ( ( P .\/ ( R ` G ) ) ./\ ( ( ( P .\/ ( R ` b ) ) ./\ ( ( N ` P ) .\/ ( R ` ( b o. `' F ) ) ) ) .\/ ( R ` ( G o. `' b ) ) ) ) ) ) )

Syntax hints:   -. wn 3   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   A.wral 2912   class class class wbr 4653   |-> cmpt 4729   _I cid 5023   `'ccnv 5113   |` cres 5116   o. ccom 5118   ` cfv 5888   iota_crio 6610  (class class class)co 6650   |-> cmpt2 6652   Basecbs 15857   lecple 15948   joincjn 16944   meetcmee 16945   Atomscatm 34550   HLchlt 34637   LHypclh 35270   LTrncltrn 35387   trLctrl 35445

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-riotaBAD 34239

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-1st 7168  df-2nd 7169  df-undef 7399  df-map 7859  df-preset 16928  df-poset 16946  df-plt 16958  df-lub 16974  df-glb 16975  df-join 16976  df-meet 16977  df-p0 17039  df-p1 17040  df-lat 17046  df-clat 17108  df-oposet 34463  df-ol 34465  df-oml 34466  df-covers 34553  df-ats 34554  df-atl 34585  df-cvlat 34609  df-hlat 34638  df-llines 34784  df-lplanes 34785  df-lvols 34786  df-lines 34787  df-psubsp 34789  df-pmap 34790  df-padd 35082  df-lhyp 35274  df-laut 35275  df-ldil 35390  df-ltrn 35391  df-trl 35446

This theorem is referenced by:  cdlemk35  36200