Theorem dfrcl2 37966

Description: Reflexive closure of a relation as union with restricted identity relation. (Contributed by RP, 6-Jun-2020.)

Assertion

Ref	Expression
dfrcl2	|- r* = ( x e. _V |-> ( ( _I |` ( dom x u. ran x ) ) u. x ) )

Proof of Theorem dfrcl2

Dummy variable z is distinct from all other variables.

Step	Hyp	Ref	Expression
1		df-rcl 37965	. 2 |- r* = ( x e. _V |-> |^| { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } )
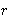
2		rabab 3223	. . . . . . . 8 |- { z e. _V | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } = { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) }
3	2	eqcomi 2631	. . . . . . 7 |- { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } = { z e. _V | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) }
4	3	inteqi 4479	. . . . . 6 |- |^| { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } = |^| { z e. _V | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) }
5	4	a1i 11	. . . . 5 |- ( x e. _V -> |^| { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } = |^| { z e. _V | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } )
6		vex 3203	. . . . . . . . . . 11 |- x e. _V
7	6	dmex 7099	. . . . . . . . . 10 |- dom x e. _V
8	6	rnex 7100	. . . . . . . . . 10 |- ran x e. _V
9	7, 8	unex 6956	. . . . . . . . 9 |- ( dom x u. ran x ) e. _V
10		resiexg 7102	. . . . . . . . 9 |- ( ( dom x u. ran x ) e. _V -> ( _I |` ( dom x u. ran x ) ) e. _V )
11	9, 10	ax-mp 5	. . . . . . . 8 |- ( _I |` ( dom x u. ran x ) ) e. _V
12	11, 6	unex 6956	. . . . . . 7 |- ( ( _I |` ( dom x u. ran x ) ) u. x ) e. _V
13	12	a1i 11	. . . . . 6 |- ( x e. _V -> ( ( _I |` ( dom x u. ran x ) ) u. x ) e. _V )
14		ssun2 3777	. . . . . . 7 |- x C_ ( ( _I |` ( dom x u. ran x ) ) u. x )
15		dmun 5331	. . . . . . . . . . . 12 |- dom ( ( _I |` ( dom x u. ran x ) ) u. x ) = ( dom ( _I |` ( dom x u. ran x ) ) u. dom x )
16		dmresi 5457	. . . . . . . . . . . . 13 |- dom ( _I |` ( dom x u. ran x ) ) = ( dom x u. ran x )
17	16	uneq1i 3763	. . . . . . . . . . . 12 |- ( dom ( _I |` ( dom x u. ran x ) ) u. dom x ) = ( ( dom x u. ran x ) u. dom x )
18		un23 3772	. . . . . . . . . . . . 13 |- ( ( dom x u. ran x ) u. dom x ) = ( ( dom x u. dom x ) u. ran x )
19		unidm 3756	. . . . . . . . . . . . . 14 |- ( dom x u. dom x ) = dom x
20	19	uneq1i 3763	. . . . . . . . . . . . 13 |- ( ( dom x u. dom x ) u. ran x ) = ( dom x u. ran x )
21	18, 20	eqtri 2644	. . . . . . . . . . . 12 |- ( ( dom x u. ran x ) u. dom x ) = ( dom x u. ran x )
22	15, 17, 21	3eqtri 2648	. . . . . . . . . . 11 |- dom ( ( _I |` ( dom x u. ran x ) ) u. x ) = ( dom x u. ran x )
23		rnun 5541	. . . . . . . . . . . 12 |- ran ( ( _I |` ( dom x u. ran x ) ) u. x ) = ( ran ( _I |` ( dom x u. ran x ) ) u. ran x )
24		rnresi 5479	. . . . . . . . . . . . 13 |- ran ( _I |` ( dom x u. ran x ) ) = ( dom x u. ran x )
25	24	uneq1i 3763	. . . . . . . . . . . 12 |- ( ran ( _I |` ( dom x u. ran x ) ) u. ran x ) = ( ( dom x u. ran x ) u. ran x )
26		unass 3770	. . . . . . . . . . . . 13 |- ( ( dom x u. ran x ) u. ran x ) = ( dom x u. ( ran x u. ran x ) )
27		unidm 3756	. . . . . . . . . . . . . 14 |- ( ran x u. ran x ) = ran x
28	27	uneq2i 3764	. . . . . . . . . . . . 13 |- ( dom x u. ( ran x u. ran x ) ) = ( dom x u. ran x )
29	26, 28	eqtri 2644	. . . . . . . . . . . 12 |- ( ( dom x u. ran x ) u. ran x ) = ( dom x u. ran x )
30	23, 25, 29	3eqtri 2648	. . . . . . . . . . 11 |- ran ( ( _I |` ( dom x u. ran x ) ) u. x ) = ( dom x u. ran x )
31	22, 30	uneq12i 3765	. . . . . . . . . 10 |- ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) = ( ( dom x u. ran x ) u. ( dom x u. ran x ) )
32		unidm 3756	. . . . . . . . . 10 |- ( ( dom x u. ran x ) u. ( dom x u. ran x ) ) = ( dom x u. ran x )
33	31, 32	eqtri 2644	. . . . . . . . 9 |- ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) = ( dom x u. ran x )
34	33	reseq2i 5393	. . . . . . . 8 |- ( _I |` ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) = ( _I |` ( dom x u. ran x ) )
35		ssun1 3776	. . . . . . . 8 |- ( _I |` ( dom x u. ran x ) ) C_ ( ( _I |` ( dom x u. ran x ) ) u. x )
36	34, 35	eqsstri 3635	. . . . . . 7 |- ( _I |` ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) C_ ( ( _I |` ( dom x u. ran x ) ) u. x )
37	14, 36	pm3.2i 471	. . . . . 6 |- ( x C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) /\ ( _I |` ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) )
38		dmeq 5324	. . . . . . . . . . 11 |- ( z = ( ( _I |` ( dom x u. ran x ) ) u. x ) -> dom z = dom ( ( _I |` ( dom x u. ran x ) ) u. x ) )
39		rneq 5351	. . . . . . . . . . 11 |- ( z = ( ( _I |` ( dom x u. ran x ) ) u. x ) -> ran z = ran ( ( _I |` ( dom x u. ran x ) ) u. x ) )
40	38, 39	uneq12d 3768	. . . . . . . . . 10 |- ( z = ( ( _I |` ( dom x u. ran x ) ) u. x ) -> ( dom z u. ran z ) = ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) )
41	40	reseq2d 5396	. . . . . . . . 9 |- ( z = ( ( _I |` ( dom x u. ran x ) ) u. x ) -> ( _I |` ( dom z u. ran z ) ) = ( _I |` ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) )
42		id 22	. . . . . . . . 9 |- ( z = ( ( _I |` ( dom x u. ran x ) ) u. x ) -> z = ( ( _I |` ( dom x u. ran x ) ) u. x ) )
43	41, 42	sseq12d 3634	. . . . . . . 8 |- ( z = ( ( _I |` ( dom x u. ran x ) ) u. x ) -> ( ( _I |` ( dom z u. ran z ) ) C_ z <-> ( _I |` ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) ) )
44	43	cleq2lem 37914	. . . . . . 7 |- ( z = ( ( _I |` ( dom x u. ran x ) ) u. x ) -> ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) <-> ( x C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) /\ ( _I |` ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) )
45	44	intminss 4503	. . . . . 6 |- ( ( ( ( _I |` ( dom x u. ran x ) ) u. x ) e. _V /\ ( x C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) /\ ( _I |` ( dom ( ( _I |` ( dom x u. ran x ) ) u. x ) u. ran ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) ) ) -> |^| { z e. _V | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) )
46	13, 37, 45	sylancl 694	. . . . 5 |- ( x e. _V -> |^| { z e. _V | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) )
47	5, 46	eqsstrd 3639	. . . 4 |- ( x e. _V -> |^| { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } C_ ( ( _I |` ( dom x u. ran x ) ) u. x ) )
48		dmss 5323	. . . . . . . . . . . . . . . 16 |- ( x C_ z -> dom x C_ dom z )
49		rnss 5354	. . . . . . . . . . . . . . . 16 |- ( x C_ z -> ran x C_ ran z )
50		unss12 3785	. . . . . . . . . . . . . . . 16 |- ( ( dom x C_ dom z /\ ran x C_ ran z ) -> ( dom x u. ran x ) C_ ( dom z u. ran z ) )
51	48, 49, 50	syl2anc 693	. . . . . . . . . . . . . . 15 |- ( x C_ z -> ( dom x u. ran x ) C_ ( dom z u. ran z ) )
52		dfss 3589	. . . . . . . . . . . . . . 15 |- ( ( dom x u. ran x ) C_ ( dom z u. ran z ) <-> ( dom x u. ran x ) = ( ( dom x u. ran x ) i^i ( dom z u. ran z ) ) )
53	51, 52	sylib 208	. . . . . . . . . . . . . 14 |- ( x C_ z -> ( dom x u. ran x ) = ( ( dom x u. ran x ) i^i ( dom z u. ran z ) ) )
54		incom 3805	. . . . . . . . . . . . . 14 |- ( ( dom x u. ran x ) i^i ( dom z u. ran z ) ) = ( ( dom z u. ran z ) i^i ( dom x u. ran x ) )
55	53, 54	syl6eq 2672	. . . . . . . . . . . . 13 |- ( x C_ z -> ( dom x u. ran x ) = ( ( dom z u. ran z ) i^i ( dom x u. ran x ) ) )
56	55	reseq2d 5396	. . . . . . . . . . . 12 |- ( x C_ z -> ( _I |` ( dom x u. ran x ) ) = ( _I |` ( ( dom z u. ran z ) i^i ( dom x u. ran x ) ) ) )
57		resres 5409	. . . . . . . . . . . 12 |- ( ( _I |` ( dom z u. ran z ) ) |` ( dom x u. ran x ) ) = ( _I |` ( ( dom z u. ran z ) i^i ( dom x u. ran x ) ) )
58	56, 57	syl6eqr 2674	. . . . . . . . . . 11 |- ( x C_ z -> ( _I |` ( dom x u. ran x ) ) = ( ( _I |` ( dom z u. ran z ) ) |` ( dom x u. ran x ) ) )
59		resss 5422	. . . . . . . . . . . 12 |- ( ( _I |` ( dom z u. ran z ) ) |` ( dom x u. ran x ) ) C_ ( _I |` ( dom z u. ran z ) )
60	59	a1i 11	. . . . . . . . . . 11 |- ( x C_ z -> ( ( _I |` ( dom z u. ran z ) ) |` ( dom x u. ran x ) ) C_ ( _I |` ( dom z u. ran z ) ) )
61	58, 60	eqsstrd 3639	. . . . . . . . . 10 |- ( x C_ z -> ( _I |` ( dom x u. ran x ) ) C_ ( _I |` ( dom z u. ran z ) ) )
62	61	adantr 481	. . . . . . . . 9 |- ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) -> ( _I |` ( dom x u. ran x ) ) C_ ( _I |` ( dom z u. ran z ) ) )
63		simpr 477	. . . . . . . . 9 |- ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) -> ( _I |` ( dom z u. ran z ) ) C_ z )
64	62, 63	sstrd 3613	. . . . . . . 8 |- ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) -> ( _I |` ( dom x u. ran x ) ) C_ z )
65		simpl 473	. . . . . . . 8 |- ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) -> x C_ z )
66	64, 65	unssd 3789	. . . . . . 7 |- ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) -> ( ( _I |` ( dom x u. ran x ) ) u. x ) C_ z )
67	66	ax-gen 1722	. . . . . 6 |- A. z ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) -> ( ( _I |` ( dom x u. ran x ) ) u. x ) C_ z )
68	67	a1i 11	. . . . 5 |- ( x e. _V -> A. z ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) -> ( ( _I |` ( dom x u. ran x ) ) u. x ) C_ z ) )
69		ssintab 4494	. . . . 5 |- ( ( ( _I |` ( dom x u. ran x ) ) u. x ) C_ |^| { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } <-> A. z ( ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) -> ( ( _I |` ( dom x u. ran x ) ) u. x ) C_ z ) )
70	68, 69	sylibr 224	. . . 4 |- ( x e. _V -> ( ( _I |` ( dom x u. ran x ) ) u. x ) C_ |^| { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } )
71	47, 70	eqssd 3620	. . 3 |- ( x e. _V -> |^| { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } = ( ( _I |` ( dom x u. ran x ) ) u. x ) )
72	71	mpteq2ia 4740	. 2 |- ( x e. _V |-> |^| { z | ( x C_ z /\ ( _I |` ( dom z u. ran z ) ) C_ z ) } ) = ( x e. _V |-> ( ( _I |` ( dom x u. ran x ) ) u. x ) )
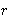
73	1, 72	eqtri 2644	1 |- r* = ( x e. _V |-> ( ( _I |` ( dom x u. ran x ) ) u. x ) )

Syntax hints:   -> wi 4   /\ wa 384   A.wal 1481   = wceq 1483   e. wcel 1990   {cab 2608   {crab 2916   _Vcvv 3200   u. cun 3572   i^i cin 3573   C_ wss 3574   |^|cint 4475   |-> cmpt 4729   _I cid 5023   dom cdm 5114   ran crn 5115   |` cres 5116   r*crcl 37964

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ral 2917  df-rex 2918  df-rab 2921  df-v 3202  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-int 4476  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-rcl 37965

This theorem is referenced by:  dfrcl3  37967