| Step | Hyp | Ref
| Expression |
|---|
| 1 | | ltexnqi 6599 |
. . . . 5
    
             |
| 2 | 1 | adantl 271 |
. . . 4
            
   
    
            |
| 3 | | subhalfnqq 6604 |
. . . . . 6
                  |
| 4 | 3 | ad2antrl 473 |
. . . . 5
                 
                         
      |
| 5 | | archrecnq 6853 |
. . . . . . 7
                   ![] ]](rbrack.gif)      |
| 6 | 5 | ad2antrl 473 |
. . . . . 6
                  
                        
                       ![] ]](rbrack.gif)      |
| 7 | | simprr 498 |
. . . . . . . . . . . 12
        
                                               
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)      |
| 8 | | nnnq 6612 |
. . . . . . . . . . . . . . 15
            ![] ]](rbrack.gif)     |
| 9 | | recclnq 6582 |
. . . . . . . . . . . . . . 15
        ![] ]](rbrack.gif)              ![] ]](rbrack.gif)   
  |
| 10 | 8, 9 | syl 14 |
. . . . . . . . . . . . . 14
               ![] ]](rbrack.gif)      |
| 11 | 10 | ad2antrl 473 |
. . . . . . . . . . . . 13
        
                                               
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)      |
| 12 | | simplrl 501 |
. . . . . . . . . . . . 13
        
                                               
            ![] ]](rbrack.gif)            |
| 13 | | lt2addnq 6594 |
. . . . . . . . . . . . 13
             ![] ]](rbrack.gif)     
   
           ![] ]](rbrack.gif)           
           ![] ]](rbrack.gif)               ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)             ![] ]](rbrack.gif)            |
| 14 | 11, 12, 11, 12, 13 | syl22anc 1170 |
. . . . . . . . . . . 12
        
                                               
            ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)             ![] ]](rbrack.gif)            |
| 15 | 7, 7, 14 | mp2and 423 |
. . . . . . . . . . 11
        
                                               
            ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)             ![] ]](rbrack.gif)           |
| 16 | | simplrr 502 |
. . . . . . . . . . 11
        
                                               
            ![] ]](rbrack.gif)                |
| 17 | | ltsonq 6588 |
. . . . . . . . . . . 12
  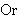  |
| 18 | | ltrelnq 6555 |
. . . . . . . . . . . 12
  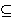      |
| 19 | 17, 18 | sotri 4740 |
. . . . . . . . . . 11
             ![] ]](rbrack.gif)             ![] ]](rbrack.gif)          
        
          ![] ]](rbrack.gif)             ![] ]](rbrack.gif)       |
| 20 | 15, 16, 19 | syl2anc 403 |
. . . . . . . . . 10
        
                                               
            ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)             ![] ]](rbrack.gif)       |
| 21 | | simplrl 501 |
. . . . . . . . . . 11
            
   
    
    |
| 22 | 21 | ad3antrrr 475 |
. . . . . . . . . 10
        
                                               
            ![] ]](rbrack.gif)            |
| 23 | | ltanqi 6592 |
. . . . . . . . . 10
             ![] ]](rbrack.gif)             ![] ]](rbrack.gif)      
   
              ![] ]](rbrack.gif)             ![] ]](rbrack.gif)            |
| 24 | 20, 22, 23 | syl2anc 403 |
. . . . . . . . 9
        
                                               
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)     
      |
| 25 | | simprr 498 |
. . . . . . . . . 10
                 
                            |
| 26 | 25 | ad2antrr 471 |
. . . . . . . . 9
        
                                               
            ![] ]](rbrack.gif)                |
| 27 | 24, 26 | breqtrd 3809 |
. . . . . . . 8
        
                                               
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)     
  |
| 28 | | addclnq 6565 |
. . . . . . . . . . 11
            ![] ]](rbrack.gif)               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)             ![] ]](rbrack.gif)       |
| 29 | 11, 11, 28 | syl2anc 403 |
. . . . . . . . . 10
        
                                               
            ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)             ![] ]](rbrack.gif)       |
| 30 | | addclnq 6565 |
. . . . . . . . . 10
                 ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)        |
| 31 | 22, 29, 30 | syl2anc 403 |
. . . . . . . . 9
        
                                               
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)        |
| 32 | | simplrr 502 |
. . . . . . . . . 10
            
   
    
    |
| 33 | 32 | ad3antrrr 475 |
. . . . . . . . 9
        
                                               
            ![] ]](rbrack.gif)            |
| 34 | | caucvgpr.f |
. . . . . . . . . . . 12
          |
| 35 | 34 | ad5antr 479 |
. . . . . . . . . . 11
        
                                               
            ![] ]](rbrack.gif)              |
| 36 | | simprl 497 |
. . . . . . . . . . 11
        
                                               
            ![] ]](rbrack.gif)            |
| 37 | 35, 36 | ffvelrnd 5324 |
. . . . . . . . . 10
        
                                               
            ![] ]](rbrack.gif)                |
| 38 | | addclnq 6565 |
. . . . . . . . . 10
                    ![] ]](rbrack.gif)   
                   ![] ]](rbrack.gif)       |
| 39 | 37, 11, 38 | syl2anc 403 |
. . . . . . . . 9
        
                                               
            ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)       |
| 40 | | sowlin 4075 |
. . . . . . . . . 10
    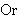                 ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                            ![] ]](rbrack.gif)        
              ![] ]](rbrack.gif)             ![] ]](rbrack.gif)     
                ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)         |
| 41 | 17, 40 | mpan 414 |
. . . . . . . . 9
                ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                            ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)             ![] ]](rbrack.gif)      
               ![] ]](rbrack.gif)             ![] ]](rbrack.gif)     
                ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)         |
| 42 | 31, 33, 39, 41 | syl3anc 1169 |
. . . . . . . 8
        
                                               
            ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)         |
| 43 | 27, 42 | mpd 13 |
. . . . . . 7
        
                                               
            ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)        |
| 44 | 22 | adantr 270 |
. . . . . . . . . 10
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)          |
| 45 | | simplrl 501 |
. . . . . . . . . . 11
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)          |
| 46 | | simpr 108 |
. . . . . . . . . . . . 13
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)             ![] ]](rbrack.gif)     
                ![] ]](rbrack.gif)     |
| 47 | 11 | adantr 270 |
. . . . . . . . . . . . . . 15
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)               ![] ]](rbrack.gif)      |
| 48 | | addassnqg 6572 |
. . . . . . . . . . . . . . 15
                ![] ]](rbrack.gif)   
           ![] ]](rbrack.gif)                    ![] ]](rbrack.gif)              ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)             ![] ]](rbrack.gif)      |
| 49 | 44, 47, 47, 48 | syl3anc 1169 |
. . . . . . . . . . . . . 14
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)              ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)             ![] ]](rbrack.gif)      |
| 50 | 49 | breq1d 3795 |
. . . . . . . . . . . . 13
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                    ![] ]](rbrack.gif)              ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)      |
| 51 | 46, 50 | mpbird 165 |
. . . . . . . . . . . 12
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)              ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)     |
| 52 | | ltanqg 6590 |
. . . . . . . . . . . . . 14
        
           
             |
| 53 | 52 | adantl 271 |
. . . . . . . . . . . . 13
                     
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)            
                          |
| 54 | | addclnq 6565 |
. . . . . . . . . . . . . 14
                ![] ]](rbrack.gif)   
               ![] ]](rbrack.gif)       |
| 55 | 44, 47, 54 | syl2anc 403 |
. . . . . . . . . . . . 13
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)       |
| 56 | 37 | adantr 270 |
. . . . . . . . . . . . 13
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)              |
| 57 | | addcomnqg 6571 |
. . . . . . . . . . . . . 14
        
               |
| 58 | 57 | adantl 271 |
. . . . . . . . . . . . 13
                     
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)            
   
            |
| 59 | 53, 55, 56, 47, 58 | caovord2d 5690 |
. . . . . . . . . . . 12
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)          
             ![] ]](rbrack.gif)              ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)      |
| 60 | 51, 59 | mpbird 165 |
. . . . . . . . . . 11
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)           |
| 61 | | opeq1 3570 |
. . . . . . . . . . . . . . . 16
          
       |
| 62 | 61 | eceq1d 6165 |
. . . . . . . . . . . . . . 15
            ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   |
| 63 | 62 | fveq2d 5202 |
. . . . . . . . . . . . . 14
               ![] ]](rbrack.gif)             ![] ]](rbrack.gif)    |
| 64 | 63 | oveq2d 5548 |
. . . . . . . . . . . . 13
                  ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)     |
| 65 | | fveq2 5198 |
. . . . . . . . . . . . 13
                  |
| 66 | 64, 65 | breq12d 3798 |
. . . . . . . . . . . 12
                   ![] ]](rbrack.gif)          
            ![] ]](rbrack.gif)            |
| 67 | 66 | rspcev 2701 |
. . . . . . . . . . 11
                   ![] ]](rbrack.gif)             
              ![] ]](rbrack.gif)           |
| 68 | 45, 60, 67 | syl2anc 403 |
. . . . . . . . . 10
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)           |
| 69 | | oveq1 5539 |
. . . . . . . . . . . . 13
                  ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)     |
| 70 | 69 | breq1d 3795 |
. . . . . . . . . . . 12
                   ![] ]](rbrack.gif)          
            ![] ]](rbrack.gif)            |
| 71 | 70 | rexbidv 2369 |
. . . . . . . . . . 11
        
              ![] ]](rbrack.gif)          
                ![] ]](rbrack.gif)            |
| 72 | | caucvgpr.lim |
. . . . . . . . . . . . 13
                         ![] ]](rbrack.gif)             
                       ![] ]](rbrack.gif)        |
| 73 | 72 | fveq2i 5201 |
. . . . . . . . . . . 12
                  
             ![] ]](rbrack.gif)             
                       ![] ]](rbrack.gif)         |
| 74 | | nqex 6553 |
. . . . . . . . . . . . . 14
    |
| 75 | 74 | rabex 3922 |
. . . . . . . . . . . . 13
        
             ![] ]](rbrack.gif)             |
| 76 | 74 | rabex 3922 |
. . . . . . . . . . . . 13
                          ![] ]](rbrack.gif)      
  |
| 77 | 75, 76 | op1st 5793 |
. . . . . . . . . . . 12
                          ![] ]](rbrack.gif)                  
                  ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)           |
| 78 | 73, 77 | eqtri 2101 |
. . . . . . . . . . 11
             
              ![] ]](rbrack.gif)           |
| 79 | 71, 78 | elrab2 2751 |
. . . . . . . . . 10
              
                ![] ]](rbrack.gif)            |
| 80 | 44, 68, 79 | sylanbrc 408 |
. . . . . . . . 9
                
   
                        
                        ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)              |
| 81 | 80 | ex 113 |
. . . . . . . 8
        
                                               
            ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)    
         |
| 82 | 33 | adantr 270 |
. . . . . . . . . 10
                
   
                        
                        ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)            |
| 83 | 65, 63 | oveq12d 5550 |
. . . . . . . . . . . . 13
                      ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)     |
| 84 | 83 | breq1d 3795 |
. . . . . . . . . . . 12
                       ![] ]](rbrack.gif)      
                ![] ]](rbrack.gif)        |
| 85 | 84 | rspcev 2701 |
. . . . . . . . . . 11
                       ![] ]](rbrack.gif)         
                  ![] ]](rbrack.gif)       |
| 86 | 36, 85 | sylan 277 |
. . . . . . . . . 10
                
   
                        
                        ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                            ![] ]](rbrack.gif)       |
| 87 | | breq2 3789 |
. . . . . . . . . . . 12
                       ![] ]](rbrack.gif)      
                ![] ]](rbrack.gif)        |
| 88 | 87 | rexbidv 2369 |
. . . . . . . . . . 11
        
                  ![] ]](rbrack.gif)      
                    ![] ]](rbrack.gif)        |
| 89 | 72 | fveq2i 5201 |
. . . . . . . . . . . 12
                  
             ![] ]](rbrack.gif)             
                       ![] ]](rbrack.gif)         |
| 90 | 75, 76 | op2nd 5794 |
. . . . . . . . . . . 12
                          ![] ]](rbrack.gif)                  
                  ![] ]](rbrack.gif)                                   ![] ]](rbrack.gif)       |
| 91 | 89, 90 | eqtri 2101 |
. . . . . . . . . . 11
             
                  ![] ]](rbrack.gif)       |
| 92 | 88, 91 | elrab2 2751 |
. . . . . . . . . 10
              
                    ![] ]](rbrack.gif)        |
| 93 | 82, 86, 92 | sylanbrc 408 |
. . . . . . . . 9
                
   
                        
                        ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                |
| 94 | 93 | ex 113 |
. . . . . . . 8
        
                                               
            ![] ]](rbrack.gif)                         ![] ]](rbrack.gif)                |
| 95 | 81, 94 | orim12d 732 |
. . . . . . 7
        
                                               
            ![] ]](rbrack.gif)                       ![] ]](rbrack.gif)             ![] ]](rbrack.gif)                      ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                           |
| 96 | 43, 95 | mpd 13 |
. . . . . 6
        
                                               
            ![] ]](rbrack.gif)                          |
| 97 | 6, 96 | rexlimddv 2481 |
. . . . 5
                  
                        
                            |
| 98 | 4, 97 | rexlimddv 2481 |
. . . 4
                 
                                      |
| 99 | 2, 98 | rexlimddv 2481 |
. . 3
            
   
    
                  |
| 100 | 99 | ex 113 |
. 2
    
                                   |
| 101 | 100 | ralrimivva 2443 |
1
                                    |