Theorem ltsonq 6588

Description: 'Less than' is a strict ordering on positive fractions. (Contributed by NM, 19-Feb-1996.) (Revised by Mario Carneiro, 4-May-2013.)

Assertion

Ref	Expression
ltsonq	|- <Q Or Q.

Proof of Theorem ltsonq

Dummy variables a b c d e f x y z w are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		df-nqqs 6538	. . . . . 6 |- Q. = ( ( N. X. N. ) /. ~Q )
2		id 19	. . . . . . . 8 |- ( [ <. z , w >. ] ~Q = x -> [ <. z , w >. ] ~Q = x )
3	2, 2	breq12d 3798	. . . . . . 7 |- ( [ <. z , w >. ] ~Q = x -> ( [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> x <Q x ) )
4	3	notbid 624	. . . . . 6 |- ( [ <. z , w >. ] ~Q = x -> ( -. [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> -. x <Q x ) )
5		ltsopi 6510	. . . . . . . 8 |- <N Or N.
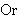6		ltrelpi 6514	. . . . . . . 8 |- <N C_ ( N. X. N. )
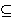7	5, 6	soirri 4739	. . . . . . 7 |- -. ( w .N z ) <N ( w .N z )
8		ordpipqqs 6564	. . . . . . . . 9 |- ( ( ( z e. N. /\ w e. N. ) /\ ( z e. N. /\ w e. N. ) ) -> ( [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> ( z .N w ) <N ( w .N z ) ) )
9	8	anidms 389	. . . . . . . 8 |- ( ( z e. N. /\ w e. N. ) -> ( [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> ( z .N w ) <N ( w .N z ) ) )
10		mulcompig 6521	. . . . . . . . 9 |- ( ( z e. N. /\ w e. N. ) -> ( z .N w ) = ( w .N z ) )
11	10	breq1d 3795	. . . . . . . 8 |- ( ( z e. N. /\ w e. N. ) -> ( ( z .N w ) <N ( w .N z ) <-> ( w .N z ) <N ( w .N z ) ) )
12	9, 11	bitrd 186	. . . . . . 7 |- ( ( z e. N. /\ w e. N. ) -> ( [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> ( w .N z ) <N ( w .N z ) ) )
13	7, 12	mtbiri 632	. . . . . 6 |- ( ( z e. N. /\ w e. N. ) -> -. [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q )
14	1, 4, 13	ecoptocl 6216	. . . . 5 |- ( x e. Q. -> -. x <Q x )
15	14	adantl 271	. . . 4 |- ( ( T. /\ x e. Q. ) -> -. x <Q x )
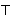16		breq1 3788	. . . . . . . 8 |- ( [ <. a , b >. ] ~Q = x -> ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q <-> x <Q [ <. c , d >. ] ~Q ) )
17	16	anbi1d 452	. . . . . . 7 |- ( [ <. a , b >. ] ~Q = x -> ( ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) <-> ( x <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) )
18		breq1 3788	. . . . . . 7 |- ( [ <. a , b >. ] ~Q = x -> ( [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q <-> x <Q [ <. e , f >. ] ~Q ) )
19	17, 18	imbi12d 232	. . . . . 6 |- ( [ <. a , b >. ] ~Q = x -> ( ( ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q ) <-> ( ( x <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> x <Q [ <. e , f >. ] ~Q ) ) )
20		breq2 3789	. . . . . . . 8 |- ( [ <. c , d >. ] ~Q = y -> ( x <Q [ <. c , d >. ] ~Q <-> x <Q y ) )
21		breq1 3788	. . . . . . . 8 |- ( [ <. c , d >. ] ~Q = y -> ( [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q <-> y <Q [ <. e , f >. ] ~Q ) )
22	20, 21	anbi12d 456	. . . . . . 7 |- ( [ <. c , d >. ] ~Q = y -> ( ( x <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) <-> ( x <Q y /\ y <Q [ <. e , f >. ] ~Q ) ) )
23	22	imbi1d 229	. . . . . 6 |- ( [ <. c , d >. ] ~Q = y -> ( ( ( x <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> x <Q [ <. e , f >. ] ~Q ) <-> ( ( x <Q y /\ y <Q [ <. e , f >. ] ~Q ) -> x <Q [ <. e , f >. ] ~Q ) ) )
24		breq2 3789	. . . . . . . 8 |- ( [ <. e , f >. ] ~Q = z -> ( y <Q [ <. e , f >. ] ~Q <-> y <Q z ) )
25	24	anbi2d 451	. . . . . . 7 |- ( [ <. e , f >. ] ~Q = z -> ( ( x <Q y /\ y <Q [ <. e , f >. ] ~Q ) <-> ( x <Q y /\ y <Q z ) ) )
26		breq2 3789	. . . . . . 7 |- ( [ <. e , f >. ] ~Q = z -> ( x <Q [ <. e , f >. ] ~Q <-> x <Q z ) )
27	25, 26	imbi12d 232	. . . . . 6 |- ( [ <. e , f >. ] ~Q = z -> ( ( ( x <Q y /\ y <Q [ <. e , f >. ] ~Q ) -> x <Q [ <. e , f >. ] ~Q ) <-> ( ( x <Q y /\ y <Q z ) -> x <Q z ) ) )
28		ordpipqqs 6564	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q <-> ( a .N d ) <N ( b .N c ) ) )
29	28	3adant3 958	. . . . . . . . . . . . . . 15 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q <-> ( a .N d ) <N ( b .N c ) ) )
30		simp1l 962	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> a e. N. )
31		simp2r 965	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> d e. N. )
32		mulclpi 6518	. . . . . . . . . . . . . . . . 17 |- ( ( a e. N. /\ d e. N. ) -> ( a .N d ) e. N. )
33	30, 31, 32	syl2anc 403	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( a .N d ) e. N. )
34		simp1r 963	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> b e. N. )
35		simp2l 964	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> c e. N. )
36		mulclpi 6518	. . . . . . . . . . . . . . . . 17 |- ( ( b e. N. /\ c e. N. ) -> ( b .N c ) e. N. )
37	34, 35, 36	syl2anc 403	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( b .N c ) e. N. )
38		simp3r 967	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> f e. N. )
39		mulclpi 6518	. . . . . . . . . . . . . . . . 17 |- ( ( c e. N. /\ f e. N. ) -> ( c .N f ) e. N. )
40	35, 38, 39	syl2anc 403	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( c .N f ) e. N. )
41		ltmpig 6529	. . . . . . . . . . . . . . . 16 |- ( ( ( a .N d ) e. N. /\ ( b .N c ) e. N. /\ ( c .N f ) e. N. ) -> ( ( a .N d ) <N ( b .N c ) <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) ) )
42	33, 37, 40, 41	syl3anc 1169	. . . . . . . . . . . . . . 15 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( a .N d ) <N ( b .N c ) <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) ) )
43	29, 42	bitrd 186	. . . . . . . . . . . . . 14 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) ) )
44	43	biimpa 290	. . . . . . . . . . . . 13 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) )
45	44	adantrr 462	. . . . . . . . . . . 12 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) )
46		mulcompig 6521	. . . . . . . . . . . . . 14 |- ( ( ( c .N f ) e. N. /\ ( b .N c ) e. N. ) -> ( ( c .N f ) .N ( b .N c ) ) = ( ( b .N c ) .N ( c .N f ) ) )
47	40, 37, 46	syl2anc 403	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N f ) .N ( b .N c ) ) = ( ( b .N c ) .N ( c .N f ) ) )
48	47	adantr 270	. . . . . . . . . . . 12 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N f ) .N ( b .N c ) ) = ( ( b .N c ) .N ( c .N f ) ) )
49	45, 48	breqtrd 3809	. . . . . . . . . . 11 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( c .N f ) ) )
50		ordpipqqs 6564	. . . . . . . . . . . . . . 15 |- ( ( ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( c .N f ) <N ( d .N e ) ) )
51	50	3adant1 956	. . . . . . . . . . . . . 14 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( c .N f ) <N ( d .N e ) ) )
52		simp3l 966	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> e e. N. )
53		mulclpi 6518	. . . . . . . . . . . . . . . 16 |- ( ( d e. N. /\ e e. N. ) -> ( d .N e ) e. N. )
54	31, 52, 53	syl2anc 403	. . . . . . . . . . . . . . 15 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( d .N e ) e. N. )
55		ltmpig 6529	. . . . . . . . . . . . . . 15 |- ( ( ( c .N f ) e. N. /\ ( d .N e ) e. N. /\ ( b .N c ) e. N. ) -> ( ( c .N f ) <N ( d .N e ) <-> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
56	40, 54, 37, 55	syl3anc 1169	. . . . . . . . . . . . . 14 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N f ) <N ( d .N e ) <-> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
57	51, 56	bitrd 186	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
58	57	biimpa 290	. . . . . . . . . . . 12 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) )
59	58	adantrl 461	. . . . . . . . . . 11 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) )
60	5, 6	sotri 4740	. . . . . . . . . . 11 |- ( ( ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( c .N f ) ) /\ ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( d .N e ) ) )
61	49, 59, 60	syl2anc 403	. . . . . . . . . 10 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( d .N e ) ) )
62		mulcompig 6521	. . . . . . . . . . . . . . 15 |- ( ( x e. N. /\ y e. N. ) -> ( x .N y ) = ( y .N x ) )
63	62	adantl 271	. . . . . . . . . . . . . 14 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( x e. N. /\ y e. N. ) ) -> ( x .N y ) = ( y .N x ) )
64		mulasspig 6522	. . . . . . . . . . . . . . 15 |- ( ( x e. N. /\ y e. N. /\ z e. N. ) -> ( ( x .N y ) .N z ) = ( x .N ( y .N z ) ) )
65	64	adantl 271	. . . . . . . . . . . . . 14 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( x e. N. /\ y e. N. /\ z e. N. ) ) -> ( ( x .N y ) .N z ) = ( x .N ( y .N z ) ) )
66		mulclpi 6518	. . . . . . . . . . . . . . 15 |- ( ( x e. N. /\ y e. N. ) -> ( x .N y ) e. N. )
67	66	adantl 271	. . . . . . . . . . . . . 14 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( x e. N. /\ y e. N. ) ) -> ( x .N y ) e. N. )
68	35, 31, 30, 63, 65, 38, 67	caov411d 5706	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N d ) .N ( a .N f ) ) = ( ( a .N d ) .N ( c .N f ) ) )
69	63, 33, 40	caovcomd 5677	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( a .N d ) .N ( c .N f ) ) = ( ( c .N f ) .N ( a .N d ) ) )
70	68, 69	eqtrd 2113	. . . . . . . . . . . 12 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N d ) .N ( a .N f ) ) = ( ( c .N f ) .N ( a .N d ) ) )
71	35, 31, 34, 63, 65, 52, 67	caov4d 5705	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N d ) .N ( b .N e ) ) = ( ( c .N b ) .N ( d .N e ) ) )
72	63, 35, 34	caovcomd 5677	. . . . . . . . . . . . . 14 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( c .N b ) = ( b .N c ) )
73	72	oveq1d 5547	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N b ) .N ( d .N e ) ) = ( ( b .N c ) .N ( d .N e ) ) )
74	71, 73	eqtrd 2113	. . . . . . . . . . . 12 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N d ) .N ( b .N e ) ) = ( ( b .N c ) .N ( d .N e ) ) )
75	70, 74	breq12d 3798	. . . . . . . . . . 11 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
76	75	adantr 270	. . . . . . . . . 10 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
77	61, 76	mpbird 165	. . . . . . . . 9 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) )
78		mulclpi 6518	. . . . . . . . . . . 12 |- ( ( a e. N. /\ f e. N. ) -> ( a .N f ) e. N. )
79	30, 38, 78	syl2anc 403	. . . . . . . . . . 11 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( a .N f ) e. N. )
80		mulclpi 6518	. . . . . . . . . . . 12 |- ( ( b e. N. /\ e e. N. ) -> ( b .N e ) e. N. )
81	34, 52, 80	syl2anc 403	. . . . . . . . . . 11 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( b .N e ) e. N. )
82		mulclpi 6518	. . . . . . . . . . . 12 |- ( ( c e. N. /\ d e. N. ) -> ( c .N d ) e. N. )
83	35, 31, 82	syl2anc 403	. . . . . . . . . . 11 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( c .N d ) e. N. )
84		ltmpig 6529	. . . . . . . . . . 11 |- ( ( ( a .N f ) e. N. /\ ( b .N e ) e. N. /\ ( c .N d ) e. N. ) -> ( ( a .N f ) <N ( b .N e ) <-> ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) ) )
85	79, 81, 83, 84	syl3anc 1169	. . . . . . . . . 10 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( a .N f ) <N ( b .N e ) <-> ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) ) )
86	85	adantr 270	. . . . . . . . 9 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( a .N f ) <N ( b .N e ) <-> ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) ) )
87	77, 86	mpbird 165	. . . . . . . 8 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( a .N f ) <N ( b .N e ) )
88		ordpipqqs 6564	. . . . . . . . . 10 |- ( ( ( a e. N. /\ b e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( a .N f ) <N ( b .N e ) ) )
89	88	3adant2 957	. . . . . . . . 9 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( a .N f ) <N ( b .N e ) ) )
90	89	adantr 270	. . . . . . . 8 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( a .N f ) <N ( b .N e ) ) )
91	87, 90	mpbird 165	. . . . . . 7 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q )
92	91	ex 113	. . . . . 6 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q ) )
93	1, 19, 23, 27, 92	3ecoptocl 6218	. . . . 5 |- ( ( x e. Q. /\ y e. Q. /\ z e. Q. ) -> ( ( x <Q y /\ y <Q z ) -> x <Q z ) )
94	93	adantl 271	. . . 4 |- ( ( T. /\ ( x e. Q. /\ y e. Q. /\ z e. Q. ) ) -> ( ( x <Q y /\ y <Q z ) -> x <Q z ) )
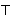
95	15, 94	ispod 4059	. . 3 |- ( T. -> <Q Po Q. )
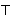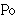96		nqtri3or 6586	. . . 4 |- ( ( x e. Q. /\ y e. Q. ) -> ( x <Q y \/ x = y \/ y <Q x ) )
97	96	adantl 271	. . 3 |- ( ( T. /\ ( x e. Q. /\ y e. Q. ) ) -> ( x <Q y \/ x = y \/ y <Q x ) )
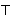
98	95, 97	issod 4074	. 2 |- ( T. -> <Q Or Q. )
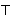99	98	trud 1293	1 |- <Q Or Q.

Syntax hints:   -. wn 3   -> wi 4   /\ wa 102   <-> wb 103   \/ w3o 918   /\ w3a 919   = wceq 1284   T. wtru 1285   e. wcel 1433   <.cop 3401   class class class wbr 3785   Or wor 4050  (class class class)co 5532   [cec 6127   N.cnpi 6462   .N cmi 6464   <N clti 6465   ~Q ceq 6469   Q.cnq 6470   <Q cltq 6475

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-in1 576  ax-in2 577  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-13 1444  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-coll 3893  ax-sep 3896  ax-nul 3904  ax-pow 3948  ax-pr 3964  ax-un 4188  ax-setind 4280  ax-iinf 4329

This theorem depends on definitions:  df-bi 115  df-dc 776  df-3or 920  df-3an 921  df-tru 1287  df-fal 1290  df-nf 1390  df-sb 1686  df-eu 1944  df-mo 1945  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ne 2246  df-ral 2353  df-rex 2354  df-reu 2355  df-rab 2357  df-v 2603  df-sbc 2816  df-csb 2909  df-dif 2975  df-un 2977  df-in 2979  df-ss 2986  df-nul 3252  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-uni 3602  df-int 3637  df-iun 3680  df-br 3786  df-opab 3840  df-mpt 3841  df-tr 3876  df-eprel 4044  df-id 4048  df-po 4051  df-iso 4052  df-iord 4121  df-on 4123  df-suc 4126  df-iom 4332  df-xp 4369  df-rel 4370  df-cnv 4371  df-co 4372  df-dm 4373  df-rn 4374  df-res 4375  df-ima 4376  df-iota 4887  df-fun 4924  df-fn 4925  df-f 4926  df-f1 4927  df-fo 4928  df-f1o 4929  df-fv 4930  df-ov 5535  df-oprab 5536  df-mpt2 5537  df-1st 5787  df-2nd 5788  df-recs 5943  df-irdg 5980  df-oadd 6028  df-omul 6029  df-er 6129  df-ec 6131  df-qs 6135  df-ni 6494  df-mi 6496  df-lti 6497  df-enq 6537  df-nqqs 6538  df-ltnqqs 6543

This theorem is referenced by:  nqtric  6589  lt2addnq  6594  lt2mulnq  6595  ltbtwnnqq  6605  prarloclemarch2  6609  genplt2i  6700  genpdisj  6713  addlocprlemgt  6724  nqprdisj  6734  nqprloc  6735  addnqprlemfl  6749  addnqprlemfu  6750  prmuloclemcalc  6755  mulnqprlemfl  6765  mulnqprlemfu  6766  distrlem4prl  6774  distrlem4pru  6775  ltsopr  6786  ltexprlemopl  6791  ltexprlemopu  6793  ltexprlemdisj  6796  ltexprlemru  6802  recexprlemlol  6816  recexprlemupu  6818  recexprlemdisj  6820  recexprlemss1l  6825  recexprlemss1u  6826  cauappcvgprlemopl  6836  cauappcvgprlemlol  6837  cauappcvgprlemupu  6839  cauappcvgprlemdisj  6841  cauappcvgprlemloc  6842  cauappcvgprlemladdfu  6844  cauappcvgprlemladdru  6846  cauappcvgprlemladdrl  6847  caucvgprlemk  6855  caucvgprlemnkj  6856  caucvgprlemnbj  6857  caucvgprlemm  6858  caucvgprlemopl  6859  caucvgprlemlol  6860  caucvgprlemupu  6862  caucvgprlemloc  6865  caucvgprlemladdfu  6867  caucvgprprlemloccalc  6874  caucvgprprlemml  6884  caucvgprprlemopl  6887