Theorem ltexprlemopl 6791

Description: The lower cut of our constructed difference is open. Lemma for ltexpri 6803. (Contributed by Jim Kingdon, 21-Dec-2019.)

Hypothesis

Ref	Expression
ltexprlem.1	|- C = <. { x e. Q. | E. y ( y e. ( 2nd ` A ) /\ ( y +Q x ) e. ( 1st ` B ) ) } , { x e. Q. | E. y ( y e. ( 1st ` A ) /\ ( y +Q x ) e. ( 2nd ` B ) ) } >.

Assertion

Ref	Expression
ltexprlemopl	|- ( ( A <P B /\ q e. Q. /\ q e. ( 1st ` C ) ) -> E. r e. Q. ( q <Q r /\ r e. ( 1st ` C ) ) )

Distinct variable groups:   x, y, q, r, A   x, B, y, q, r   x, C, y, q, r

Proof of Theorem ltexprlemopl

Dummy variable s is distinct from all other variables.

Step	Hyp	Ref	Expression
1		ltexprlem.1	. . . . 5 |- C = <. { x e. Q. | E. y ( y e. ( 2nd ` A ) /\ ( y +Q x ) e. ( 1st ` B ) ) } , { x e. Q. | E. y ( y e. ( 1st ` A ) /\ ( y +Q x ) e. ( 2nd ` B ) ) } >.
2	1	ltexprlemell 6788	. . . 4 |- ( q e. ( 1st ` C ) <-> ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
3	2	simprbi 269	. . 3 |- ( q e. ( 1st ` C ) -> E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) )
4		19.42v 1827	. . . . . . . 8 |- ( E. y ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) <-> ( A <P B /\ E. y ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) )
5		19.42v 1827	. . . . . . . . 9 |- ( E. y ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) <-> ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
6	5	anbi2i 444	. . . . . . . 8 |- ( ( A <P B /\ E. y ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) <-> ( A <P B /\ ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) )
7	4, 6	bitri 182	. . . . . . 7 |- ( E. y ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) <-> ( A <P B /\ ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) )
8		ltrelpr 6695	. . . . . . . . . . . . . 14 |- <P C_ ( P. X. P. )
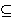9	8	brel 4410	. . . . . . . . . . . . 13 |- ( A <P B -> ( A e. P. /\ B e. P. ) )
10	9	simprd 112	. . . . . . . . . . . 12 |- ( A <P B -> B e. P. )
11		prop 6665	. . . . . . . . . . . . 13 |- ( B e. P. -> <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. )
12		prnmaxl 6678	. . . . . . . . . . . . 13 |- ( ( <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. /\ ( y +Q q ) e. ( 1st ` B ) ) -> E. s e. ( 1st ` B ) ( y +Q q ) <Q s )
13	11, 12	sylan 277	. . . . . . . . . . . 12 |- ( ( B e. P. /\ ( y +Q q ) e. ( 1st ` B ) ) -> E. s e. ( 1st ` B ) ( y +Q q ) <Q s )
14	10, 13	sylan 277	. . . . . . . . . . 11 |- ( ( A <P B /\ ( y +Q q ) e. ( 1st ` B ) ) -> E. s e. ( 1st ` B ) ( y +Q q ) <Q s )
15	14	adantrl 461	. . . . . . . . . 10 |- ( ( A <P B /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) -> E. s e. ( 1st ` B ) ( y +Q q ) <Q s )
16	15	adantrl 461	. . . . . . . . 9 |- ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) -> E. s e. ( 1st ` B ) ( y +Q q ) <Q s )
17	9	simpld 110	. . . . . . . . . . . . . . 15 |- ( A <P B -> A e. P. )
18	17	ad2antrr 471	. . . . . . . . . . . . . 14 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> A e. P. )
19		simplrr 502	. . . . . . . . . . . . . . 15 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) )
20	19	simpld 110	. . . . . . . . . . . . . 14 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> y e. ( 2nd ` A ) )
21		prop 6665	. . . . . . . . . . . . . . 15 |- ( A e. P. -> <. ( 1st ` A ) , ( 2nd ` A ) >. e. P. )
22		elprnqu 6672	. . . . . . . . . . . . . . 15 |- ( ( <. ( 1st ` A ) , ( 2nd ` A ) >. e. P. /\ y e. ( 2nd ` A ) ) -> y e. Q. )
23	21, 22	sylan 277	. . . . . . . . . . . . . 14 |- ( ( A e. P. /\ y e. ( 2nd ` A ) ) -> y e. Q. )
24	18, 20, 23	syl2anc 403	. . . . . . . . . . . . 13 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> y e. Q. )
25		simplrl 501	. . . . . . . . . . . . 13 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> q e. Q. )
26		ltaddnq 6597	. . . . . . . . . . . . 13 |- ( ( y e. Q. /\ q e. Q. ) -> y <Q ( y +Q q ) )
27	24, 25, 26	syl2anc 403	. . . . . . . . . . . 12 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> y <Q ( y +Q q ) )
28		simprr 498	. . . . . . . . . . . 12 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> ( y +Q q ) <Q s )
29		ltsonq 6588	. . . . . . . . . . . . 13 |- <Q Or Q.
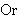30		ltrelnq 6555	. . . . . . . . . . . . 13 |- <Q C_ ( Q. X. Q. )
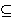31	29, 30	sotri 4740	. . . . . . . . . . . 12 |- ( ( y <Q ( y +Q q ) /\ ( y +Q q ) <Q s ) -> y <Q s )
32	27, 28, 31	syl2anc 403	. . . . . . . . . . 11 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> y <Q s )
33	10	ad2antrr 471	. . . . . . . . . . . . 13 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> B e. P. )
34		simprl 497	. . . . . . . . . . . . 13 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> s e. ( 1st ` B ) )
35		elprnql 6671	. . . . . . . . . . . . . 14 |- ( ( <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. /\ s e. ( 1st ` B ) ) -> s e. Q. )
36	11, 35	sylan 277	. . . . . . . . . . . . 13 |- ( ( B e. P. /\ s e. ( 1st ` B ) ) -> s e. Q. )
37	33, 34, 36	syl2anc 403	. . . . . . . . . . . 12 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> s e. Q. )
38		ltexnqq 6598	. . . . . . . . . . . 12 |- ( ( y e. Q. /\ s e. Q. ) -> ( y <Q s <-> E. r e. Q. ( y +Q r ) = s ) )
39	24, 37, 38	syl2anc 403	. . . . . . . . . . 11 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> ( y <Q s <-> E. r e. Q. ( y +Q r ) = s ) )
40	32, 39	mpbid 145	. . . . . . . . . 10 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> E. r e. Q. ( y +Q r ) = s )
41		simplrr 502	. . . . . . . . . . . . . . 15 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> ( y +Q q ) <Q s )
42		simprr 498	. . . . . . . . . . . . . . 15 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> ( y +Q r ) = s )
43	41, 42	breqtrrd 3811	. . . . . . . . . . . . . 14 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> ( y +Q q ) <Q ( y +Q r ) )
44	25	adantr 270	. . . . . . . . . . . . . . 15 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> q e. Q. )
45		simprl 497	. . . . . . . . . . . . . . 15 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> r e. Q. )
46	24	adantr 270	. . . . . . . . . . . . . . 15 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> y e. Q. )
47		ltanqg 6590	. . . . . . . . . . . . . . 15 |- ( ( q e. Q. /\ r e. Q. /\ y e. Q. ) -> ( q <Q r <-> ( y +Q q ) <Q ( y +Q r ) ) )
48	44, 45, 46, 47	syl3anc 1169	. . . . . . . . . . . . . 14 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> ( q <Q r <-> ( y +Q q ) <Q ( y +Q r ) ) )
49	43, 48	mpbird 165	. . . . . . . . . . . . 13 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> q <Q r )
50	20	adantr 270	. . . . . . . . . . . . . 14 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> y e. ( 2nd ` A ) )
51		simplrl 501	. . . . . . . . . . . . . . 15 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> s e. ( 1st ` B ) )
52	42, 51	eqeltrd 2155	. . . . . . . . . . . . . 14 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> ( y +Q r ) e. ( 1st ` B ) )
53	50, 52	jca 300	. . . . . . . . . . . . 13 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) )
54	49, 45, 53	jca32 303	. . . . . . . . . . . 12 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ ( r e. Q. /\ ( y +Q r ) = s ) ) -> ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
55	54	expr 367	. . . . . . . . . . 11 |- ( ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) /\ r e. Q. ) -> ( ( y +Q r ) = s -> ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) ) )
56	55	reximdva 2463	. . . . . . . . . 10 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> ( E. r e. Q. ( y +Q r ) = s -> E. r e. Q. ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) ) )
57	40, 56	mpd 13	. . . . . . . . 9 |- ( ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) /\ ( s e. ( 1st ` B ) /\ ( y +Q q ) <Q s ) ) -> E. r e. Q. ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
58	16, 57	rexlimddv 2481	. . . . . . . 8 |- ( ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) -> E. r e. Q. ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
59	58	eximi 1531	. . . . . . 7 |- ( E. y ( A <P B /\ ( q e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) -> E. y E. r e. Q. ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
60	7, 59	sylbir 133	. . . . . 6 |- ( ( A <P B /\ ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) -> E. y E. r e. Q. ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
61		rexcom4 2622	. . . . . 6 |- ( E. r e. Q. E. y ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) <-> E. y E. r e. Q. ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
62	60, 61	sylibr 132	. . . . 5 |- ( ( A <P B /\ ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) -> E. r e. Q. E. y ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
63		19.42v 1827	. . . . . . 7 |- ( E. y ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) <-> ( q <Q r /\ E. y ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
64		19.42v 1827	. . . . . . . 8 |- ( E. y ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) <-> ( r e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) )
65	64	anbi2i 444	. . . . . . 7 |- ( ( q <Q r /\ E. y ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) <-> ( q <Q r /\ ( r e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
66	63, 65	bitri 182	. . . . . 6 |- ( E. y ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) <-> ( q <Q r /\ ( r e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
67	66	rexbii 2373	. . . . 5 |- ( E. r e. Q. E. y ( q <Q r /\ ( r e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) <-> E. r e. Q. ( q <Q r /\ ( r e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
68	62, 67	sylib 120	. . . 4 |- ( ( A <P B /\ ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) -> E. r e. Q. ( q <Q r /\ ( r e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
69	1	ltexprlemell 6788	. . . . . 6 |- ( r e. ( 1st ` C ) <-> ( r e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) )
70	69	anbi2i 444	. . . . 5 |- ( ( q <Q r /\ r e. ( 1st ` C ) ) <-> ( q <Q r /\ ( r e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
71	70	rexbii 2373	. . . 4 |- ( E. r e. Q. ( q <Q r /\ r e. ( 1st ` C ) ) <-> E. r e. Q. ( q <Q r /\ ( r e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q r ) e. ( 1st ` B ) ) ) ) )
72	68, 71	sylibr 132	. . 3 |- ( ( A <P B /\ ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) -> E. r e. Q. ( q <Q r /\ r e. ( 1st ` C ) ) )
73	3, 72	sylanr2 397	. 2 |- ( ( A <P B /\ ( q e. Q. /\ q e. ( 1st ` C ) ) ) -> E. r e. Q. ( q <Q r /\ r e. ( 1st ` C ) ) )
74	73	3impb 1134	1 |- ( ( A <P B /\ q e. Q. /\ q e. ( 1st ` C ) ) -> E. r e. Q. ( q <Q r /\ r e. ( 1st ` C ) ) )

Syntax hints:   -> wi 4   /\ wa 102   <-> wb 103   /\ w3a 919   = wceq 1284   E.wex 1421   e. wcel 1433   E.wrex 2349   {crab 2352   <.cop 3401   class class class wbr 3785   ` cfv 4922  (class class class)co 5532   1stc1st 5785   2ndc2nd 5786   Q.cnq 6470   +Q cplq 6472   <Q cltq 6475   P.cnp 6481   <P cltp 6485

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-in1 576  ax-in2 577  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-13 1444  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-coll 3893  ax-sep 3896  ax-nul 3904  ax-pow 3948  ax-pr 3964  ax-un 4188  ax-setind 4280  ax-iinf 4329

This theorem depends on definitions:  df-bi 115  df-dc 776  df-3or 920  df-3an 921  df-tru 1287  df-fal 1290  df-nf 1390  df-sb 1686  df-eu 1944  df-mo 1945  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ne 2246  df-ral 2353  df-rex 2354  df-reu 2355  df-rab 2357  df-v 2603  df-sbc 2816  df-csb 2909  df-dif 2975  df-un 2977  df-in 2979  df-ss 2986  df-nul 3252  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-uni 3602  df-int 3637  df-iun 3680  df-br 3786  df-opab 3840  df-mpt 3841  df-tr 3876  df-eprel 4044  df-id 4048  df-po 4051  df-iso 4052  df-iord 4121  df-on 4123  df-suc 4126  df-iom 4332  df-xp 4369  df-rel 4370  df-cnv 4371  df-co 4372  df-dm 4373  df-rn 4374  df-res 4375  df-ima 4376  df-iota 4887  df-fun 4924  df-fn 4925  df-f 4926  df-f1 4927  df-fo 4928  df-f1o 4929  df-fv 4930  df-ov 5535  df-oprab 5536  df-mpt2 5537  df-1st 5787  df-2nd 5788  df-recs 5943  df-irdg 5980  df-1o 6024  df-oadd 6028  df-omul 6029  df-er 6129  df-ec 6131  df-qs 6135  df-ni 6494  df-pli 6495  df-mi 6496  df-lti 6497  df-plpq 6534  df-mpq 6535  df-enq 6537  df-nqqs 6538  df-plqqs 6539  df-mqqs 6540  df-1nqqs 6541  df-ltnqqs 6543  df-inp 6656  df-iltp 6660

This theorem is referenced by:  ltexprlemrnd  6795