Theorem ltexprlemm 6790

Description: Our constructed difference is inhabited. Lemma for ltexpri 6803. (Contributed by Jim Kingdon, 17-Dec-2019.)

Hypothesis

Ref	Expression
ltexprlem.1	|- C = <. { x e. Q. | E. y ( y e. ( 2nd ` A ) /\ ( y +Q x ) e. ( 1st ` B ) ) } , { x e. Q. | E. y ( y e. ( 1st ` A ) /\ ( y +Q x ) e. ( 2nd ` B ) ) } >.

Assertion

Ref	Expression
ltexprlemm	|- ( A <P B -> ( E. q e. Q. q e. ( 1st ` C ) /\ E. r e. Q. r e. ( 2nd ` C ) ) )

Distinct variable groups:   x, y, q, r, A   x, B, y, q, r   x, C, y, q, r

Proof of Theorem ltexprlemm

Dummy variable w is distinct from all other variables.

Step	Hyp	Ref	Expression
1		ltrelpr 6695	. . . . . . . . 9 |- <P C_ ( P. X. P. )
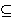2	1	brel 4410	. . . . . . . 8 |- ( A <P B -> ( A e. P. /\ B e. P. ) )
3		ltdfpr 6696	. . . . . . . . 9 |- ( ( A e. P. /\ B e. P. ) -> ( A <P B <-> E. y e. Q. ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) ) )
4	3	biimpd 142	. . . . . . . 8 |- ( ( A e. P. /\ B e. P. ) -> ( A <P B -> E. y e. Q. ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) ) )
5	2, 4	mpcom 36	. . . . . . 7 |- ( A <P B -> E. y e. Q. ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) )
6		simprrl 505	. . . . . . . . . 10 |- ( ( A <P B /\ ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) ) ) -> y e. ( 2nd ` A ) )
7	2	simprd 112	. . . . . . . . . . . . 13 |- ( A <P B -> B e. P. )
8		prop 6665	. . . . . . . . . . . . . . . . . 18 |- ( B e. P. -> <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. )
9		prnmaxl 6678	. . . . . . . . . . . . . . . . . 18 |- ( ( <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. /\ y e. ( 1st ` B ) ) -> E. w e. ( 1st ` B ) y <Q w )
10	8, 9	sylan 277	. . . . . . . . . . . . . . . . 17 |- ( ( B e. P. /\ y e. ( 1st ` B ) ) -> E. w e. ( 1st ` B ) y <Q w )
11		ltexnqi 6599	. . . . . . . . . . . . . . . . . 18 |- ( y <Q w -> E. q e. Q. ( y +Q q ) = w )
12	11	reximi 2458	. . . . . . . . . . . . . . . . 17 |- ( E. w e. ( 1st ` B ) y <Q w -> E. w e. ( 1st ` B ) E. q e. Q. ( y +Q q ) = w )
13	10, 12	syl 14	. . . . . . . . . . . . . . . 16 |- ( ( B e. P. /\ y e. ( 1st ` B ) ) -> E. w e. ( 1st ` B ) E. q e. Q. ( y +Q q ) = w )
14		df-rex 2354	. . . . . . . . . . . . . . . 16 |- ( E. w e. ( 1st ` B ) E. q e. Q. ( y +Q q ) = w <-> E. w ( w e. ( 1st ` B ) /\ E. q e. Q. ( y +Q q ) = w ) )
15	13, 14	sylib 120	. . . . . . . . . . . . . . 15 |- ( ( B e. P. /\ y e. ( 1st ` B ) ) -> E. w ( w e. ( 1st ` B ) /\ E. q e. Q. ( y +Q q ) = w ) )
16		r19.42v 2511	. . . . . . . . . . . . . . . 16 |- ( E. q e. Q. ( w e. ( 1st ` B ) /\ ( y +Q q ) = w ) <-> ( w e. ( 1st ` B ) /\ E. q e. Q. ( y +Q q ) = w ) )
17	16	exbii 1536	. . . . . . . . . . . . . . 15 |- ( E. w E. q e. Q. ( w e. ( 1st ` B ) /\ ( y +Q q ) = w ) <-> E. w ( w e. ( 1st ` B ) /\ E. q e. Q. ( y +Q q ) = w ) )
18	15, 17	sylibr 132	. . . . . . . . . . . . . 14 |- ( ( B e. P. /\ y e. ( 1st ` B ) ) -> E. w E. q e. Q. ( w e. ( 1st ` B ) /\ ( y +Q q ) = w ) )
19		eleq1 2141	. . . . . . . . . . . . . . . . 17 |- ( ( y +Q q ) = w -> ( ( y +Q q ) e. ( 1st ` B ) <-> w e. ( 1st ` B ) ) )
20	19	biimparc 293	. . . . . . . . . . . . . . . 16 |- ( ( w e. ( 1st ` B ) /\ ( y +Q q ) = w ) -> ( y +Q q ) e. ( 1st ` B ) )
21	20	reximi 2458	. . . . . . . . . . . . . . 15 |- ( E. q e. Q. ( w e. ( 1st ` B ) /\ ( y +Q q ) = w ) -> E. q e. Q. ( y +Q q ) e. ( 1st ` B ) )
22	21	exlimiv 1529	. . . . . . . . . . . . . 14 |- ( E. w E. q e. Q. ( w e. ( 1st ` B ) /\ ( y +Q q ) = w ) -> E. q e. Q. ( y +Q q ) e. ( 1st ` B ) )
23	18, 22	syl 14	. . . . . . . . . . . . 13 |- ( ( B e. P. /\ y e. ( 1st ` B ) ) -> E. q e. Q. ( y +Q q ) e. ( 1st ` B ) )
24	7, 23	sylan 277	. . . . . . . . . . . 12 |- ( ( A <P B /\ y e. ( 1st ` B ) ) -> E. q e. Q. ( y +Q q ) e. ( 1st ` B ) )
25	24	adantrl 461	. . . . . . . . . . 11 |- ( ( A <P B /\ ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) ) -> E. q e. Q. ( y +Q q ) e. ( 1st ` B ) )
26	25	adantrl 461	. . . . . . . . . 10 |- ( ( A <P B /\ ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) ) ) -> E. q e. Q. ( y +Q q ) e. ( 1st ` B ) )
27	6, 26	jca 300	. . . . . . . . 9 |- ( ( A <P B /\ ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) ) ) -> ( y e. ( 2nd ` A ) /\ E. q e. Q. ( y +Q q ) e. ( 1st ` B ) ) )
28	27	expr 367	. . . . . . . 8 |- ( ( A <P B /\ y e. Q. ) -> ( ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) -> ( y e. ( 2nd ` A ) /\ E. q e. Q. ( y +Q q ) e. ( 1st ` B ) ) ) )
29	28	reximdva 2463	. . . . . . 7 |- ( A <P B -> ( E. y e. Q. ( y e. ( 2nd ` A ) /\ y e. ( 1st ` B ) ) -> E. y e. Q. ( y e. ( 2nd ` A ) /\ E. q e. Q. ( y +Q q ) e. ( 1st ` B ) ) ) )
30	5, 29	mpd 13	. . . . . 6 |- ( A <P B -> E. y e. Q. ( y e. ( 2nd ` A ) /\ E. q e. Q. ( y +Q q ) e. ( 1st ` B ) ) )
31		r19.42v 2511	. . . . . . 7 |- ( E. q e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> ( y e. ( 2nd ` A ) /\ E. q e. Q. ( y +Q q ) e. ( 1st ` B ) ) )
32	31	rexbii 2373	. . . . . 6 |- ( E. y e. Q. E. q e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. y e. Q. ( y e. ( 2nd ` A ) /\ E. q e. Q. ( y +Q q ) e. ( 1st ` B ) ) )
33	30, 32	sylibr 132	. . . . 5 |- ( A <P B -> E. y e. Q. E. q e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) )
34		rexcom 2518	. . . . 5 |- ( E. y e. Q. E. q e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. q e. Q. E. y e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) )
35	33, 34	sylib 120	. . . 4 |- ( A <P B -> E. q e. Q. E. y e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) )
36	2	simpld 110	. . . . . . . . . . . 12 |- ( A <P B -> A e. P. )
37		prop 6665	. . . . . . . . . . . . 13 |- ( A e. P. -> <. ( 1st ` A ) , ( 2nd ` A ) >. e. P. )
38		elprnqu 6672	. . . . . . . . . . . . 13 |- ( ( <. ( 1st ` A ) , ( 2nd ` A ) >. e. P. /\ y e. ( 2nd ` A ) ) -> y e. Q. )
39	37, 38	sylan 277	. . . . . . . . . . . 12 |- ( ( A e. P. /\ y e. ( 2nd ` A ) ) -> y e. Q. )
40	36, 39	sylan 277	. . . . . . . . . . 11 |- ( ( A <P B /\ y e. ( 2nd ` A ) ) -> y e. Q. )
41	40	ex 113	. . . . . . . . . 10 |- ( A <P B -> ( y e. ( 2nd ` A ) -> y e. Q. ) )
42	41	pm4.71rd 386	. . . . . . . . 9 |- ( A <P B -> ( y e. ( 2nd ` A ) <-> ( y e. Q. /\ y e. ( 2nd ` A ) ) ) )
43	42	anbi1d 452	. . . . . . . 8 |- ( A <P B -> ( ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> ( ( y e. Q. /\ y e. ( 2nd ` A ) ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
44		anass 393	. . . . . . . 8 |- ( ( ( y e. Q. /\ y e. ( 2nd ` A ) ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
45	43, 44	syl6bb 194	. . . . . . 7 |- ( A <P B -> ( ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) )
46	45	exbidv 1746	. . . . . 6 |- ( A <P B -> ( E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. y ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) )
47	46	rexbidv 2369	. . . . 5 |- ( A <P B -> ( E. q e. Q. E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. q e. Q. E. y ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) )
48		df-rex 2354	. . . . . 6 |- ( E. y e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. y ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
49	48	rexbii 2373	. . . . 5 |- ( E. q e. Q. E. y e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. q e. Q. E. y ( y e. Q. /\ ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
50	47, 49	syl6bbr 196	. . . 4 |- ( A <P B -> ( E. q e. Q. E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. q e. Q. E. y e. Q. ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
51	35, 50	mpbird 165	. . 3 |- ( A <P B -> E. q e. Q. E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) )
52		ltexprlem.1	. . . . . 6 |- C = <. { x e. Q. | E. y ( y e. ( 2nd ` A ) /\ ( y +Q x ) e. ( 1st ` B ) ) } , { x e. Q. | E. y ( y e. ( 1st ` A ) /\ ( y +Q x ) e. ( 2nd ` B ) ) } >.
53	52	ltexprlemell 6788	. . . . 5 |- ( q e. ( 1st ` C ) <-> ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
54	53	rexbii 2373	. . . 4 |- ( E. q e. Q. q e. ( 1st ` C ) <-> E. q e. Q. ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
55		ssid 3018	. . . . 5 |- Q. C_ Q.
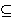56		rexss 3061	. . . . 5 |- ( Q. C_ Q. -> ( E. q e. Q. E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. q e. Q. ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) ) )
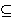
57	55, 56	ax-mp 7	. . . 4 |- ( E. q e. Q. E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) <-> E. q e. Q. ( q e. Q. /\ E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) ) )
58	54, 57	bitr4i 185	. . 3 |- ( E. q e. Q. q e. ( 1st ` C ) <-> E. q e. Q. E. y ( y e. ( 2nd ` A ) /\ ( y +Q q ) e. ( 1st ` B ) ) )
59	51, 58	sylibr 132	. 2 |- ( A <P B -> E. q e. Q. q e. ( 1st ` C ) )
60		nfv 1461	. . 3 |- F/ r A <P B
61		nfre1 2407	. . 3 |- F/ r E. r e. Q. r e. ( 2nd ` C )
62		prmu 6668	. . . . 5 |- ( <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. -> E. r e. Q. r e. ( 2nd ` B ) )
63		rexex 2410	. . . . 5 |- ( E. r e. Q. r e. ( 2nd ` B ) -> E. r r e. ( 2nd ` B ) )
64	62, 63	syl 14	. . . 4 |- ( <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. -> E. r r e. ( 2nd ` B ) )
65	7, 8, 64	3syl 17	. . 3 |- ( A <P B -> E. r r e. ( 2nd ` B ) )
66		elprnqu 6672	. . . . . . 7 |- ( ( <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. /\ r e. ( 2nd ` B ) ) -> r e. Q. )
67	8, 66	sylan 277	. . . . . 6 |- ( ( B e. P. /\ r e. ( 2nd ` B ) ) -> r e. Q. )
68	7, 67	sylan 277	. . . . 5 |- ( ( A <P B /\ r e. ( 2nd ` B ) ) -> r e. Q. )
69		prml 6667	. . . . . . . . 9 |- ( <. ( 1st ` A ) , ( 2nd ` A ) >. e. P. -> E. y e. Q. y e. ( 1st ` A ) )
70	37, 69	syl 14	. . . . . . . 8 |- ( A e. P. -> E. y e. Q. y e. ( 1st ` A ) )
71		rexex 2410	. . . . . . . 8 |- ( E. y e. Q. y e. ( 1st ` A ) -> E. y y e. ( 1st ` A ) )
72	36, 70, 71	3syl 17	. . . . . . 7 |- ( A <P B -> E. y y e. ( 1st ` A ) )
73	72	adantr 270	. . . . . 6 |- ( ( A <P B /\ r e. ( 2nd ` B ) ) -> E. y y e. ( 1st ` A ) )
74	68	3adant3 958	. . . . . . . . 9 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> r e. Q. )
75		simp3 940	. . . . . . . . . 10 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> y e. ( 1st ` A ) )
76		elprnql 6671	. . . . . . . . . . . . . . 15 |- ( ( <. ( 1st ` A ) , ( 2nd ` A ) >. e. P. /\ y e. ( 1st ` A ) ) -> y e. Q. )
77	37, 76	sylan 277	. . . . . . . . . . . . . 14 |- ( ( A e. P. /\ y e. ( 1st ` A ) ) -> y e. Q. )
78	36, 77	sylan 277	. . . . . . . . . . . . 13 |- ( ( A <P B /\ y e. ( 1st ` A ) ) -> y e. Q. )
79	78	3adant2 957	. . . . . . . . . . . 12 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> y e. Q. )
80		addcomnqg 6571	. . . . . . . . . . . 12 |- ( ( r e. Q. /\ y e. Q. ) -> ( r +Q y ) = ( y +Q r ) )
81	74, 79, 80	syl2anc 403	. . . . . . . . . . 11 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> ( r +Q y ) = ( y +Q r ) )
82		ltaddnq 6597	. . . . . . . . . . . . 13 |- ( ( r e. Q. /\ y e. Q. ) -> r <Q ( r +Q y ) )
83	74, 79, 82	syl2anc 403	. . . . . . . . . . . 12 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> r <Q ( r +Q y ) )
84		prcunqu 6675	. . . . . . . . . . . . . . 15 |- ( ( <. ( 1st ` B ) , ( 2nd ` B ) >. e. P. /\ r e. ( 2nd ` B ) ) -> ( r <Q ( r +Q y ) -> ( r +Q y ) e. ( 2nd ` B ) ) )
85	8, 84	sylan 277	. . . . . . . . . . . . . 14 |- ( ( B e. P. /\ r e. ( 2nd ` B ) ) -> ( r <Q ( r +Q y ) -> ( r +Q y ) e. ( 2nd ` B ) ) )
86	7, 85	sylan 277	. . . . . . . . . . . . 13 |- ( ( A <P B /\ r e. ( 2nd ` B ) ) -> ( r <Q ( r +Q y ) -> ( r +Q y ) e. ( 2nd ` B ) ) )
87	86	3adant3 958	. . . . . . . . . . . 12 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> ( r <Q ( r +Q y ) -> ( r +Q y ) e. ( 2nd ` B ) ) )
88	83, 87	mpd 13	. . . . . . . . . . 11 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> ( r +Q y ) e. ( 2nd ` B ) )
89	81, 88	eqeltrrd 2156	. . . . . . . . . 10 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> ( y +Q r ) e. ( 2nd ` B ) )
90		19.8a 1522	. . . . . . . . . 10 |- ( ( y e. ( 1st ` A ) /\ ( y +Q r ) e. ( 2nd ` B ) ) -> E. y ( y e. ( 1st ` A ) /\ ( y +Q r ) e. ( 2nd ` B ) ) )
91	75, 89, 90	syl2anc 403	. . . . . . . . 9 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> E. y ( y e. ( 1st ` A ) /\ ( y +Q r ) e. ( 2nd ` B ) ) )
92	74, 91	jca 300	. . . . . . . 8 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> ( r e. Q. /\ E. y ( y e. ( 1st ` A ) /\ ( y +Q r ) e. ( 2nd ` B ) ) ) )
93	52	ltexprlemelu 6789	. . . . . . . 8 |- ( r e. ( 2nd ` C ) <-> ( r e. Q. /\ E. y ( y e. ( 1st ` A ) /\ ( y +Q r ) e. ( 2nd ` B ) ) ) )
94	92, 93	sylibr 132	. . . . . . 7 |- ( ( A <P B /\ r e. ( 2nd ` B ) /\ y e. ( 1st ` A ) ) -> r e. ( 2nd ` C ) )
95	94	3expa 1138	. . . . . 6 |- ( ( ( A <P B /\ r e. ( 2nd ` B ) ) /\ y e. ( 1st ` A ) ) -> r e. ( 2nd ` C ) )
96	73, 95	exlimddv 1819	. . . . 5 |- ( ( A <P B /\ r e. ( 2nd ` B ) ) -> r e. ( 2nd ` C ) )
97		19.8a 1522	. . . . 5 |- ( ( r e. Q. /\ r e. ( 2nd ` C ) ) -> E. r ( r e. Q. /\ r e. ( 2nd ` C ) ) )
98	68, 96, 97	syl2anc 403	. . . 4 |- ( ( A <P B /\ r e. ( 2nd ` B ) ) -> E. r ( r e. Q. /\ r e. ( 2nd ` C ) ) )
99		df-rex 2354	. . . 4 |- ( E. r e. Q. r e. ( 2nd ` C ) <-> E. r ( r e. Q. /\ r e. ( 2nd ` C ) ) )
100	98, 99	sylibr 132	. . 3 |- ( ( A <P B /\ r e. ( 2nd ` B ) ) -> E. r e. Q. r e. ( 2nd ` C ) )
101	60, 61, 65, 100	exlimdd 1793	. 2 |- ( A <P B -> E. r e. Q. r e. ( 2nd ` C ) )
102	59, 101	jca 300	1 |- ( A <P B -> ( E. q e. Q. q e. ( 1st ` C ) /\ E. r e. Q. r e. ( 2nd ` C ) ) )

Syntax hints:   -> wi 4   /\ wa 102   <-> wb 103   /\ w3a 919   = wceq 1284   E.wex 1421   e. wcel 1433   E.wrex 2349   {crab 2352   C_ wss 2973   <.cop 3401   class class class wbr 3785   ` cfv 4922  (class class class)co 5532   1stc1st 5785   2ndc2nd 5786   Q.cnq 6470   +Q cplq 6472   <Q cltq 6475   P.cnp 6481   <P cltp 6485

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-in1 576  ax-in2 577  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-13 1444  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-coll 3893  ax-sep 3896  ax-nul 3904  ax-pow 3948  ax-pr 3964  ax-un 4188  ax-setind 4280  ax-iinf 4329

This theorem depends on definitions:  df-bi 115  df-dc 776  df-3or 920  df-3an 921  df-tru 1287  df-fal 1290  df-nf 1390  df-sb 1686  df-eu 1944  df-mo 1945  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ne 2246  df-ral 2353  df-rex 2354  df-reu 2355  df-rab 2357  df-v 2603  df-sbc 2816  df-csb 2909  df-dif 2975  df-un 2977  df-in 2979  df-ss 2986  df-nul 3252  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-uni 3602  df-int 3637  df-iun 3680  df-br 3786  df-opab 3840  df-mpt 3841  df-tr 3876  df-eprel 4044  df-id 4048  df-iord 4121  df-on 4123  df-suc 4126  df-iom 4332  df-xp 4369  df-rel 4370  df-cnv 4371  df-co 4372  df-dm 4373  df-rn 4374  df-res 4375  df-ima 4376  df-iota 4887  df-fun 4924  df-fn 4925  df-f 4926  df-f1 4927  df-fo 4928  df-f1o 4929  df-fv 4930  df-ov 5535  df-oprab 5536  df-mpt2 5537  df-1st 5787  df-2nd 5788  df-recs 5943  df-irdg 5980  df-1o 6024  df-oadd 6028  df-omul 6029  df-er 6129  df-ec 6131  df-qs 6135  df-ni 6494  df-pli 6495  df-mi 6496  df-lti 6497  df-plpq 6534  df-mpq 6535  df-enq 6537  df-nqqs 6538  df-plqqs 6539  df-mqqs 6540  df-1nqqs 6541  df-ltnqqs 6543  df-inp 6656  df-iltp 6660

This theorem is referenced by:  ltexprlempr  6798