cdleme7c - Mathbox for Norm Megill

	Mathbox for Norm Megill		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > cdleme7c		Structured version Visualization version Unicode version

Theorem cdleme7c 35532

Description: Part of proof of Lemma E in [Crawley] p. 113. Lemma leading to cdleme7ga 35535 and cdleme7 35536. (Contributed by NM, 7-Jun-2012.)

**Hypotheses**
Ref	Expression
cdleme4.l
cdleme4.j	$.\/$
cdleme4.m	$./\$
cdleme4.a
cdleme4.h
cdleme4.u	$.\/$ $./\$
cdleme4.f	$.\/$ $./\$ $.\/$ $.\/$ $./\$
cdleme4.g	$.\/$ $./\$ $.\/$ $.\/$ $./\$
cdleme7.v	$.\/$ $./\$

**Assertion**
Ref	Expression
cdleme7c	$/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$

**Proof of Theorem cdleme7c**
Step	Hyp	Ref	Expression
1		cdleme4.u	. . . 4 $.\/$ $./\$
2		cdleme7.v	. . . 4 $.\/$ $./\$
3	1, 2	oveq12i 6662	. . 3 $./\$ $.\/$ $./\$ $./\$ $.\/$ $./\$
4		simp11 1091	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$
5		simp12l 1174	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
6		simp13 1093	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
7		simp2l 1087	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$
8		simp32 1098	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
9		cdleme4.l	. . . . . . . . 9
10		cdleme4.j	. . . . . . . . 9 $.\/$
11		cdleme4.m	. . . . . . . . 9 $./\$
12		cdleme4.a	. . . . . . . . 9
13		cdleme4.h	. . . . . . . . 9
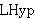14	9, 10, 11, 12, 13, 1	cdleme4 35525	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$
15	4, 5, 6, 7, 8, 14	syl131anc 1339	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
16	15	oveq1d 6665	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$
17		simp11l 1172	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
18		simp12 1092	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$
19		simp31 1097	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
20	9, 10, 11, 12, 13, 1	lhpat2 35331	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$
21	4, 18, 6, 19, 20	syl112anc 1330	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
22		simp2rl 1130	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
23		simp2ll 1128	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
24		hllat 34650	. . . . . . . . . . 11
25	17, 24	syl 17	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
26		eqid 2622	. . . . . . . . . . . 12
27	26, 10, 12	hlatjcl 34653	. . . . . . . . . . 11 $/\$ $/\$ $.\/$
28	17, 5, 6, 27	syl3anc 1326	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
29		simp11r 1173	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
30	26, 13	lhpbase 35284	. . . . . . . . . . 11
31	29, 30	syl 17	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
32	26, 9, 11	latmle2 17077	. . . . . . . . . 10 $/\$ $.\/$ $/\$ $.\/$ $./\$
33	25, 28, 31, 32	syl3anc 1326	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$
34	1, 33	syl5eqbr 4688	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
35		simp2rr 1131	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
36		nbrne2 4673	. . . . . . . 8 $/\$
37	34, 35, 36	syl2anc 693	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
38		cdleme4.f	. . . . . . . 8 $.\/$ $./\$ $.\/$ $.\/$ $./\$
39		cdleme4.g	. . . . . . . 8 $.\/$ $./\$ $.\/$ $.\/$ $./\$
40	9, 10, 11, 12, 13, 1, 38, 39	cdleme7aa 35529	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
41	9, 10, 11, 12	2llnma2 35075	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
42	17, 21, 22, 23, 37, 40, 41	syl132anc 1344	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
43	16, 42	eqtrd 2656	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
44	43	oveq1d 6665	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$ $./\$ $./\$
45		hlol 34648	. . . . . 6
46	17, 45	syl 17	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
47	26, 10, 12	hlatjcl 34653	. . . . . 6 $/\$ $/\$ $.\/$
48	17, 23, 22, 47	syl3anc 1326	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
49	26, 11	latmmdir 34522	. . . . 5 $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $./\$ $.\/$ $./\$ $.\/$ $./\$ $./\$ $.\/$ $./\$
50	46, 28, 48, 31, 49	syl13anc 1328	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$ $./\$ $.\/$ $./\$ $./\$ $.\/$ $./\$
51		eqid 2622	. . . . . 6
52	9, 11, 51, 12, 13	lhpmat 35316	. . . . 5 $/\$ $/\$ $/\$ $./\$
53	4, 7, 52	syl2anc 693	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $./\$
54	44, 50, 53	3eqtr3d 2664	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $./\$ $.\/$ $./\$
55	3, 54	syl5eq 2668	. 2 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $./\$
56		hlatl 34647	. . . 4
57	17, 56	syl 17	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
58		simp33 1099	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
59	9, 10, 11, 12, 13, 1, 38, 39, 2	cdleme7b 35531	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
60	4, 7, 22, 58, 8, 59	syl113anc 1338	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$
61	11, 51, 12	atnem0 34605	. . 3 $/\$ $/\$ $./\$
62	57, 21, 60, 61	syl3anc 1326	. 2 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $./\$
63	55, 62	mpbird 247	1 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$

Colors of variables: wff setvar class

Syntax hints:

wn 3

wi 4

wb 196 $/\$ wa 384 $/\$ w3a 1037

wceq 1483

wcel 1990

wne 2794 class class class wbr 4653

cfv 5888 (class class class)co 6650

cbs 15857

cple 15948

cjn 16944

cmee 16945

cp0 17037

clat 17045

col 34461

catm 34550

cal 34551

chlt 34637

clh 35270

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-ral 2917 df-rex 2918 df-reu 2919 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-iin 4523 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-mpt2 6655 df-1st 7168 df-2nd 7169 df-preset 16928 df-poset 16946 df-plt 16958 df-lub 16974 df-glb 16975 df-join 16976 df-meet 16977 df-p0 17039 df-p1 17040 df-lat 17046 df-clat 17108 df-oposet 34463 df-ol 34465 df-oml 34466 df-covers 34553 df-ats 34554 df-atl 34585 df-cvlat 34609 df-hlat 34638 df-psubsp 34789 df-pmap 34790 df-padd 35082 df-lhyp 35274

This theorem is referenced by: cdleme7d 35533 cdleme7ga 35535

W3C validator