Users' Mathboxes Mathbox for Norm Megill < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  MPE Home  >  Th. List  >   Mathboxes  >  cdlemefrs29bpre0 Structured version   Visualization version   Unicode version
Theorem cdlemefrs29bpre0 35684
Description: TODO fix comment. (Contributed by NM, 29-Mar-2013.)
Hypotheses
Ref Expression
cdlemefrs27.b |- B = ( Base ` K )
cdlemefrs27.l |- .<_ = ( le ` K )
cdlemefrs27.j |- .\/ = ( join ` K )
cdlemefrs27.m |- ./\ = ( meet ` K )
cdlemefrs27.a |- A = ( Atoms ` K )
cdlemefrs27.h |- H = ( LHyp ` K )
cdlemefrs27.eq |- ( s = R -> ( ph <-> ps ) )
cdlemefrs27.nb |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ P =/= Q /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> N e. B )
Assertion
Ref Expression
cdlemefrs29bpre0 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( A. s e. A ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> z = [_ R / s ]_ N ) )
Distinct variable groups:   z, s   A, s   H, s   .\/ , s   K, s   .<_ , s   P, s   Q, s   R, s   W, s   ps, s
Allowed substitution hints:   ph( z, s)   ps( z)   A( z)   B( z, s)   P( z)   Q( z)   R( z)   H( z)   .\/ ( z)   K( z)   .<_ ( z)   ./\ ( z, s)   N( z, s)   W( z)
Proof of Theorem cdlemefrs29bpre0
StepHypRef Expression
1 df-ral 2917 . . 3 |- ( A. s e. A ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> A. s ( s e. A -> ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) )
2 anass 681 . . . . . . 7 |- ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) /\ ( s .\/ ( R ./\ W ) ) = R ) <-> ( s e. A /\ ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) ) )
32imbi1i 339 . . . . . 6 |- ( ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> ( ( s e. A /\ ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) ) -> z = ( N .\/ ( R ./\ W ) ) ) )
4 impexp 462 . . . . . 6 |- ( ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) -> ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) ) )
5 impexp 462 . . . . . 6 |- ( ( ( s e. A /\ ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> ( s e. A -> ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) )
63, 4, 53bitr3ri 291 . . . . 5 |- ( ( s e. A -> ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) <-> ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) -> ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) ) )
7 simpl11 1136 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( K e. HL /\ W e. H ) )
8 simpl2r 1115 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( R e. A /\ -. R .<_ W ) )
9 cdlemefrs27.l . . . . . . . . . . . . 13 |- .<_ = ( le ` K )
10 cdlemefrs27.m . . . . . . . . . . . . 13 |- ./\ = ( meet ` K )
11 eqid 2622 . . . . . . . . . . . . 13 |- ( 0. ` K ) = ( 0. ` K )
12 cdlemefrs27.a . . . . . . . . . . . . 13 |- A = ( Atoms ` K )
13 cdlemefrs27.h . . . . . . . . . . . . 13 |- H = ( LHyp ` K )
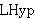149, 10, 11, 12, 13lhpmat 35316 . . . . . . . . . . . 12 |- ( ( ( K e. HL /\ W e. H ) /\ ( R e. A /\ -. R .<_ W ) ) -> ( R ./\ W ) = ( 0. ` K ) )
157, 8, 14syl2anc 693 . . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( R ./\ W ) = ( 0. ` K ) )
1615oveq2d 6666 . . . . . . . . . 10 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( s .\/ ( R ./\ W ) ) = ( s .\/ ( 0. ` K ) ) )
17 simp11l 1172 . . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> K e. HL )
18 hlol 34648 . . . . . . . . . . . . 13 |- ( K e. HL -> K e. OL )
1917, 18syl 17 . . . . . . . . . . . 12 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> K e. OL )
2019adantr 481 . . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> K e. OL )
21 simprl 794 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> s e. A )
22 cdlemefrs27.b . . . . . . . . . . . . 13 |- B = ( Base ` K )
2322, 12atbase 34576 . . . . . . . . . . . 12 |- ( s e. A -> s e. B )
2421, 23syl 17 . . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> s e. B )
25 cdlemefrs27.j . . . . . . . . . . . 12 |- .\/ = ( join ` K )
2622, 25, 11olj01 34512 . . . . . . . . . . 11 |- ( ( K e. OL /\ s e. B ) -> ( s .\/ ( 0. ` K ) ) = s )
2720, 24, 26syl2anc 693 . . . . . . . . . 10 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( s .\/ ( 0. ` K ) ) = s )
2816, 27eqtrd 2656 . . . . . . . . 9 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( s .\/ ( R ./\ W ) ) = s )
2928eqeq1d 2624 . . . . . . . 8 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( ( s .\/ ( R ./\ W ) ) = R <-> s = R ) )
3015oveq2d 6666 . . . . . . . . . 10 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( N .\/ ( R ./\ W ) ) = ( N .\/ ( 0. ` K ) ) )
31 simpl1 1064 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) )
32 simpl2l 1114 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> P =/= Q )
33 simprr 796 . . . . . . . . . . . 12 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( -. s .<_ W /\ ph ) )
34 cdlemefrs27.nb . . . . . . . . . . . 12 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ P =/= Q /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> N e. B )
3531, 32, 21, 33, 34syl112anc 1330 . . . . . . . . . . 11 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> N e. B )
3622, 25, 11olj01 34512 . . . . . . . . . . 11 |- ( ( K e. OL /\ N e. B ) -> ( N .\/ ( 0. ` K ) ) = N )
3720, 35, 36syl2anc 693 . . . . . . . . . 10 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( N .\/ ( 0. ` K ) ) = N )
3830, 37eqtrd 2656 . . . . . . . . 9 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( N .\/ ( R ./\ W ) ) = N )
3938eqeq2d 2632 . . . . . . . 8 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( z = ( N .\/ ( R ./\ W ) ) <-> z = N ) )
4029, 39imbi12d 334 . . . . . . 7 |- ( ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) /\ ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) -> ( ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) <-> ( s = R -> z = N ) ) )
4140pm5.74da 723 . . . . . 6 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) -> ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) ) <-> ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) -> ( s = R -> z = N ) ) ) )
42 impexp 462 . . . . . . 7 |- ( ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) /\ s = R ) -> z = N ) <-> ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) -> ( s = R -> z = N ) ) )
43 eqcom 2629 . . . . . . . . 9 |- ( z = N <-> N = z )
4443imbi2i 326 . . . . . . . 8 |- ( ( s = R -> z = N ) <-> ( s = R -> N = z ) )
45 simp2rl 1130 . . . . . . . . . . 11 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> R e. A )
46 simp2rr 1131 . . . . . . . . . . 11 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> -. R .<_ W )
47 simp3 1063 . . . . . . . . . . 11 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ps )
48 eleq1 2689 . . . . . . . . . . . . 13 |- ( s = R -> ( s e. A <-> R e. A ) )
49 breq1 4656 . . . . . . . . . . . . . . 15 |- ( s = R -> ( s .<_ W <-> R .<_ W ) )
5049notbid 308 . . . . . . . . . . . . . 14 |- ( s = R -> ( -. s .<_ W <-> -. R .<_ W ) )
51 cdlemefrs27.eq . . . . . . . . . . . . . 14 |- ( s = R -> ( ph <-> ps ) )
5250, 51anbi12d 747 . . . . . . . . . . . . 13 |- ( s = R -> ( ( -. s .<_ W /\ ph ) <-> ( -. R .<_ W /\ ps ) ) )
5348, 52anbi12d 747 . . . . . . . . . . . 12 |- ( s = R -> ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) <-> ( R e. A /\ ( -. R .<_ W /\ ps ) ) ) )
5453biimprcd 240 . . . . . . . . . . 11 |- ( ( R e. A /\ ( -. R .<_ W /\ ps ) ) -> ( s = R -> ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) )
5545, 46, 47, 54syl12anc 1324 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( s = R -> ( s e. A /\ ( -. s .<_ W /\ ph ) ) ) )
5655pm4.71rd 667 . . . . . . . . 9 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( s = R <-> ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) /\ s = R ) ) )
5756imbi1d 331 . . . . . . . 8 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( ( s = R -> z = N ) <-> ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) /\ s = R ) -> z = N ) ) )
5844, 57syl5rbbr 275 . . . . . . 7 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) /\ s = R ) -> z = N ) <-> ( s = R -> N = z ) ) )
5942, 58syl5bbr 274 . . . . . 6 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) -> ( s = R -> z = N ) ) <-> ( s = R -> N = z ) ) )
6041, 59bitrd 268 . . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( ( ( s e. A /\ ( -. s .<_ W /\ ph ) ) -> ( ( s .\/ ( R ./\ W ) ) = R -> z = ( N .\/ ( R ./\ W ) ) ) ) <-> ( s = R -> N = z ) ) )
616, 60syl5bb 272 . . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( ( s e. A -> ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) <-> ( s = R -> N = z ) ) )
6261albidv 1849 . . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( A. s ( s e. A -> ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) ) <-> A. s ( s = R -> N = z ) ) )
631, 62syl5bb 272 . 2 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( A. s e. A ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> A. s ( s = R -> N = z ) ) )
64 nfcv 2764 . . . . 5 |- F/_ s z
6564csbiebg 3556 . . . 4 |- ( R e. A -> ( A. s ( s = R -> N = z ) <-> [_ R / s ]_ N = z ) )
6645, 65syl 17 . . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( A. s ( s = R -> N = z ) <-> [_ R / s ]_ N = z ) )
67 eqcom 2629 . . 3 |- ( [_ R / s ]_ N = z <-> z = [_ R / s ]_ N )
6866, 67syl6bb 276 . 2 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( A. s ( s = R -> N = z ) <-> z = [_ R / s ]_ N ) )
6963, 68bitrd 268 1 |- ( ( ( ( K e. HL /\ W e. H ) /\ ( P e. A /\ -. P .<_ W ) /\ ( Q e. A /\ -. Q .<_ W ) ) /\ ( P =/= Q /\ ( R e. A /\ -. R .<_ W ) ) /\ ps ) -> ( A. s e. A ( ( ( -. s .<_ W /\ ph ) /\ ( s .\/ ( R ./\ W ) ) = R ) -> z = ( N .\/ ( R ./\ W ) ) ) <-> z = [_ R / s ]_ N ) )
Colors of variables: wff setvar class
Syntax hints:   -. wn 3   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   A.wal 1481   = wceq 1483   e. wcel 1990   =/= wne 2794   A.wral 2912   [_csb 3533   class class class wbr 4653   ` cfv 5888  (class class class)co 6650   Basecbs 15857   lecple 15948   joincjn 16944   meetcmee 16945   0.cp0 17037   OLcol 34461   Atomscatm 34550   HLchlt 34637   LHypclh 35270
This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949
This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-ral 2917  df-rex 2918  df-reu 2919  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-preset 16928  df-poset 16946  df-plt 16958  df-lub 16974  df-glb 16975  df-join 16976  df-meet 16977  df-p0 17039  df-lat 17046  df-oposet 34463  df-ol 34465  df-oml 34466  df-covers 34553  df-ats 34554  df-atl 34585  df-cvlat 34609  df-hlat 34638  df-lhyp 35274
This theorem is referenced by:  cdlemefrs29bpre1  35685  cdlemefrs32fva  35688  cdlemefr29bpre0N  35694  cdlemefs29bpre0N  35704
  Copyright terms: Public domain W3C validator