Theorem f1omvdco2 17868

Description: If exactly one of two permutations is limited to a set of points, then the composition will not be. (Contributed by Stefan O'Rear, 23-Aug-2015.)

Assertion

Ref	Expression
f1omvdco2	|- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A /\ ( dom ( F \ _I ) C_ X \/_ dom ( G \ _I ) C_ X ) ) -> -. dom ( ( F o. G ) \ _I ) C_ X )

Proof of Theorem f1omvdco2

Step	Hyp	Ref	Expression
1		excxor 1469	. . 3 |- ( ( dom ( F \ _I ) C_ X \/_ dom ( G \ _I ) C_ X ) <-> ( ( dom ( F \ _I ) C_ X /\ -. dom ( G \ _I ) C_ X ) \/ ( -. dom ( F \ _I ) C_ X /\ dom ( G \ _I ) C_ X ) ) )
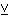
2		coass 5654	. . . . . . . . . . . 12 |- ( ( `' F o. F ) o. G ) = ( `' F o. ( F o. G ) )
3		f1ococnv1 6165	. . . . . . . . . . . . . 14 |- ( F : A -1-1-onto-> A -> ( `' F o. F ) = ( _I |` A ) )
4	3	coeq1d 5283	. . . . . . . . . . . . 13 |- ( F : A -1-1-onto-> A -> ( ( `' F o. F ) o. G ) = ( ( _I |` A ) o. G ) )
5		f1of 6137	. . . . . . . . . . . . . 14 |- ( G : A -1-1-onto-> A -> G : A --> A )
6		fcoi2 6079	. . . . . . . . . . . . . 14 |- ( G : A --> A -> ( ( _I |` A ) o. G ) = G )
7	5, 6	syl 17	. . . . . . . . . . . . 13 |- ( G : A -1-1-onto-> A -> ( ( _I |` A ) o. G ) = G )
8	4, 7	sylan9eq 2676	. . . . . . . . . . . 12 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( `' F o. F ) o. G ) = G )
9	2, 8	syl5eqr 2670	. . . . . . . . . . 11 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( `' F o. ( F o. G ) ) = G )
10	9	difeq1d 3727	. . . . . . . . . 10 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( `' F o. ( F o. G ) ) \ _I ) = ( G \ _I ) )
11	10	dmeqd 5326	. . . . . . . . 9 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> dom ( ( `' F o. ( F o. G ) ) \ _I ) = dom ( G \ _I ) )
12	11	adantr 481	. . . . . . . 8 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( F \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( ( `' F o. ( F o. G ) ) \ _I ) = dom ( G \ _I ) )
13		mvdco 17865	. . . . . . . . 9 |- dom ( ( `' F o. ( F o. G ) ) \ _I ) C_ ( dom ( `' F \ _I ) u. dom ( ( F o. G ) \ _I ) )
14		f1omvdcnv 17864	. . . . . . . . . . . 12 |- ( F : A -1-1-onto-> A -> dom ( `' F \ _I ) = dom ( F \ _I ) )
15	14	ad2antrr 762	. . . . . . . . . . 11 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( F \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( `' F \ _I ) = dom ( F \ _I ) )
16		simprl 794	. . . . . . . . . . 11 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( F \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( F \ _I ) C_ X )
17	15, 16	eqsstrd 3639	. . . . . . . . . 10 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( F \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( `' F \ _I ) C_ X )
18		simprr 796	. . . . . . . . . 10 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( F \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( ( F o. G ) \ _I ) C_ X )
19	17, 18	unssd 3789	. . . . . . . . 9 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( F \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> ( dom ( `' F \ _I ) u. dom ( ( F o. G ) \ _I ) ) C_ X )
20	13, 19	syl5ss 3614	. . . . . . . 8 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( F \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( ( `' F o. ( F o. G ) ) \ _I ) C_ X )
21	12, 20	eqsstr3d 3640	. . . . . . 7 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( F \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( G \ _I ) C_ X )
22	21	expr 643	. . . . . 6 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ dom ( F \ _I ) C_ X ) -> ( dom ( ( F o. G ) \ _I ) C_ X -> dom ( G \ _I ) C_ X ) )
23	22	con3d 148	. . . . 5 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ dom ( F \ _I ) C_ X ) -> ( -. dom ( G \ _I ) C_ X -> -. dom ( ( F o. G ) \ _I ) C_ X ) )
24	23	expimpd 629	. . . 4 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( dom ( F \ _I ) C_ X /\ -. dom ( G \ _I ) C_ X ) -> -. dom ( ( F o. G ) \ _I ) C_ X ) )
25		coass 5654	. . . . . . . . . . . . 13 |- ( ( F o. G ) o. `' G ) = ( F o. ( G o. `' G ) )
26		f1ococnv2 6163	. . . . . . . . . . . . . . 15 |- ( G : A -1-1-onto-> A -> ( G o. `' G ) = ( _I |` A ) )
27	26	coeq2d 5284	. . . . . . . . . . . . . 14 |- ( G : A -1-1-onto-> A -> ( F o. ( G o. `' G ) ) = ( F o. ( _I |` A ) ) )
28		f1of 6137	. . . . . . . . . . . . . . 15 |- ( F : A -1-1-onto-> A -> F : A --> A )
29		fcoi1 6078	. . . . . . . . . . . . . . 15 |- ( F : A --> A -> ( F o. ( _I |` A ) ) = F )
30	28, 29	syl 17	. . . . . . . . . . . . . 14 |- ( F : A -1-1-onto-> A -> ( F o. ( _I |` A ) ) = F )
31	27, 30	sylan9eqr 2678	. . . . . . . . . . . . 13 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( F o. ( G o. `' G ) ) = F )
32	25, 31	syl5eq 2668	. . . . . . . . . . . 12 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( F o. G ) o. `' G ) = F )
33	32	difeq1d 3727	. . . . . . . . . . 11 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( ( F o. G ) o. `' G ) \ _I ) = ( F \ _I ) )
34	33	dmeqd 5326	. . . . . . . . . 10 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> dom ( ( ( F o. G ) o. `' G ) \ _I ) = dom ( F \ _I ) )
35	34	adantr 481	. . . . . . . . 9 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( G \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( ( ( F o. G ) o. `' G ) \ _I ) = dom ( F \ _I ) )
36		mvdco 17865	. . . . . . . . . 10 |- dom ( ( ( F o. G ) o. `' G ) \ _I ) C_ ( dom ( ( F o. G ) \ _I ) u. dom ( `' G \ _I ) )
37		simprr 796	. . . . . . . . . . 11 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( G \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( ( F o. G ) \ _I ) C_ X )
38		f1omvdcnv 17864	. . . . . . . . . . . . 13 |- ( G : A -1-1-onto-> A -> dom ( `' G \ _I ) = dom ( G \ _I ) )
39	38	ad2antlr 763	. . . . . . . . . . . 12 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( G \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( `' G \ _I ) = dom ( G \ _I ) )
40		simprl 794	. . . . . . . . . . . 12 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( G \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( G \ _I ) C_ X )
41	39, 40	eqsstrd 3639	. . . . . . . . . . 11 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( G \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( `' G \ _I ) C_ X )
42	37, 41	unssd 3789	. . . . . . . . . 10 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( G \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> ( dom ( ( F o. G ) \ _I ) u. dom ( `' G \ _I ) ) C_ X )
43	36, 42	syl5ss 3614	. . . . . . . . 9 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( G \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( ( ( F o. G ) o. `' G ) \ _I ) C_ X )
44	35, 43	eqsstr3d 3640	. . . . . . . 8 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ ( dom ( G \ _I ) C_ X /\ dom ( ( F o. G ) \ _I ) C_ X ) ) -> dom ( F \ _I ) C_ X )
45	44	expr 643	. . . . . . 7 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ dom ( G \ _I ) C_ X ) -> ( dom ( ( F o. G ) \ _I ) C_ X -> dom ( F \ _I ) C_ X ) )
46	45	con3d 148	. . . . . 6 |- ( ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) /\ dom ( G \ _I ) C_ X ) -> ( -. dom ( F \ _I ) C_ X -> -. dom ( ( F o. G ) \ _I ) C_ X ) )
47	46	expimpd 629	. . . . 5 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( dom ( G \ _I ) C_ X /\ -. dom ( F \ _I ) C_ X ) -> -. dom ( ( F o. G ) \ _I ) C_ X ) )
48	47	ancomsd 470	. . . 4 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( -. dom ( F \ _I ) C_ X /\ dom ( G \ _I ) C_ X ) -> -. dom ( ( F o. G ) \ _I ) C_ X ) )
49	24, 48	jaod 395	. . 3 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( ( dom ( F \ _I ) C_ X /\ -. dom ( G \ _I ) C_ X ) \/ ( -. dom ( F \ _I ) C_ X /\ dom ( G \ _I ) C_ X ) ) -> -. dom ( ( F o. G ) \ _I ) C_ X ) )
50	1, 49	syl5bi 232	. 2 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A ) -> ( ( dom ( F \ _I ) C_ X \/_ dom ( G \ _I ) C_ X ) -> -. dom ( ( F o. G ) \ _I ) C_ X ) )
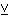
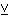
51	50	3impia 1261	1 |- ( ( F : A -1-1-onto-> A /\ G : A -1-1-onto-> A /\ ( dom ( F \ _I ) C_ X \/_ dom ( G \ _I ) C_ X ) ) -> -. dom ( ( F o. G ) \ _I ) C_ X )

Syntax hints:   -. wn 3   -> wi 4   \/ wo 383   /\ wa 384   /\ w3a 1037   \/_ wxo 1464   = wceq 1483   \ cdif 3571   u. cun 3572   C_ wss 3574   _I cid 5023   `'ccnv 5113   dom cdm 5114   |` cres 5116   o. ccom 5118   -->wf 5884   -1-1-onto->wf1o 5887

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3an 1039  df-xor 1465  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-ral 2917  df-rex 2918  df-rab 2921  df-v 3202  df-sbc 3436  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-br 4654  df-opab 4713  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896

This theorem is referenced by:  f1omvdco3  17869