Theorem bezoutlemmain 10387

Description: Lemma for Bézout's identity. This is the main result which we prove by induction and which represents the application of the Extended Euclidean algorithm. (Contributed by Jim Kingdon, 30-Dec-2021.)

Hypotheses

Ref	Expression
bezout.is-bezout	|- ( ph <-> E. s e. ZZ E. t e. ZZ r = ( ( A x. s ) + ( B x. t ) ) )
bezout.sub-gcd	|- ( ps <-> A. z e. NN0 ( z || r -> ( z || x /\ z || y ) ) )
bezout.a	|- ( th -> A e. NN0 )
bezout.b	|- ( th -> B e. NN0 )

Assertion

Ref	Expression
bezoutlemmain	|- ( th -> A. x e. NN0 ( [ x / r ] ph -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( ps /\ ph ) ) ) )

Distinct variable groups:   ph, s, t, x, y, z   ps, s, t, z   s, r, t, x, y, z, th   A, r, s, t   B, r, s, t

Allowed substitution hints:   ph( r)   ps( x, y, r)   A( x, y, z)   B( x, y, z)

Proof of Theorem bezoutlemmain

Dummy variables a w are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		sbequ 1761	. . . . . . 7 |- ( w = z -> ( [ w / r ] ph <-> [ z / r ] ph ) )
2	1	anbi2d 451	. . . . . 6 |- ( w = z -> ( ( th /\ [ w / r ] ph ) <-> ( th /\ [ z / r ] ph ) ) )
3		sbequ 1761	. . . . . . . . . 10 |- ( w = z -> ( [ w / x ] ps <-> [ z / x ] ps ) )
4	3	anbi1d 452	. . . . . . . . 9 |- ( w = z -> ( ( [ w / x ] ps /\ ph ) <-> ( [ z / x ] ps /\ ph ) ) )
5	4	rexbidv 2369	. . . . . . . 8 |- ( w = z -> ( E. r e. NN0 ( [ w / x ] ps /\ ph ) <-> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) )
6	5	imbi2d 228	. . . . . . 7 |- ( w = z -> ( ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) <-> ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) )
7	6	ralbidv 2368	. . . . . 6 |- ( w = z -> ( A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) <-> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) )
8	2, 7	imbi12d 232	. . . . 5 |- ( w = z -> ( ( ( th /\ [ w / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) ) <-> ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) )
9		sbequ 1761	. . . . . . 7 |- ( w = x -> ( [ w / r ] ph <-> [ x / r ] ph ) )
10	9	anbi2d 451	. . . . . 6 |- ( w = x -> ( ( th /\ [ w / r ] ph ) <-> ( th /\ [ x / r ] ph ) ) )
11		sbequ12r 1695	. . . . . . . . . 10 |- ( w = x -> ( [ w / x ] ps <-> ps ) )
12	11	anbi1d 452	. . . . . . . . 9 |- ( w = x -> ( ( [ w / x ] ps /\ ph ) <-> ( ps /\ ph ) ) )
13	12	rexbidv 2369	. . . . . . . 8 |- ( w = x -> ( E. r e. NN0 ( [ w / x ] ps /\ ph ) <-> E. r e. NN0 ( ps /\ ph ) ) )
14	13	imbi2d 228	. . . . . . 7 |- ( w = x -> ( ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) <-> ( [ y / r ] ph -> E. r e. NN0 ( ps /\ ph ) ) ) )
15	14	ralbidv 2368	. . . . . 6 |- ( w = x -> ( A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) <-> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( ps /\ ph ) ) ) )
16	10, 15	imbi12d 232	. . . . 5 |- ( w = x -> ( ( ( th /\ [ w / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) ) <-> ( ( th /\ [ x / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( ps /\ ph ) ) ) ) )
17		nfv 1461	. . . . . . . . . . 11 |- F/ y w e. NN0
18		nfcv 2219	. . . . . . . . . . . 12 |- F/_ y ( 0 ... ( w - 1 ) )
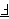19		nfv 1461	. . . . . . . . . . . . 13 |- F/ y ( th /\ [ z / r ] ph )
20		nfra1 2397	. . . . . . . . . . . . 13 |- F/ y A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) )
21	19, 20	nfim 1504	. . . . . . . . . . . 12 |- F/ y ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) )
22	18, 21	nfralxy 2402	. . . . . . . . . . 11 |- F/ y A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) )
23	17, 22	nfan 1497	. . . . . . . . . 10 |- F/ y ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) )
24		nfv 1461	. . . . . . . . . 10 |- F/ y ( th /\ [ w / r ] ph )
25	23, 24	nfan 1497	. . . . . . . . 9 |- F/ y ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) )
26		nfv 1461	. . . . . . . . 9 |- F/ y w = 0
27	25, 26	nfan 1497	. . . . . . . 8 |- F/ y ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ w = 0 )
28		simplr 496	. . . . . . . . . 10 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ w = 0 ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> y e. NN0 )
29		nfv 1461	. . . . . . . . . . . . . 14 |- F/ r A. z e. NN0 ( z || y -> ( z || 0 /\ z || y ) )
30		breq2 3789	. . . . . . . . . . . . . . . 16 |- ( r = y -> ( z || r <-> z || y ) )
31	30	imbi1d 229	. . . . . . . . . . . . . . 15 |- ( r = y -> ( ( z || r -> ( z || 0 /\ z || y ) ) <-> ( z || y -> ( z || 0 /\ z || y ) ) ) )
32	31	ralbidv 2368	. . . . . . . . . . . . . 14 |- ( r = y -> ( A. z e. NN0 ( z || r -> ( z || 0 /\ z || y ) ) <-> A. z e. NN0 ( z || y -> ( z || 0 /\ z || y ) ) ) )
33	29, 32	sbie 1714	. . . . . . . . . . . . 13 |- ( [ y / r ] A. z e. NN0 ( z || r -> ( z || 0 /\ z || y ) ) <-> A. z e. NN0 ( z || y -> ( z || 0 /\ z || y ) ) )
34		nn0z 8371	. . . . . . . . . . . . . . . 16 |- ( z e. NN0 -> z e. ZZ )
35		dvds0 10210	. . . . . . . . . . . . . . . 16 |- ( z e. ZZ -> z || 0 )
36	34, 35	syl 14	. . . . . . . . . . . . . . 15 |- ( z e. NN0 -> z || 0 )
37	36	biantrurd 299	. . . . . . . . . . . . . 14 |- ( z e. NN0 -> ( z || y <-> ( z || 0 /\ z || y ) ) )
38	37	biimpd 142	. . . . . . . . . . . . 13 |- ( z e. NN0 -> ( z || y -> ( z || 0 /\ z || y ) ) )
39	33, 38	mprgbir 2421	. . . . . . . . . . . 12 |- [ y / r ] A. z e. NN0 ( z || r -> ( z || 0 /\ z || y ) )
40		nfv 1461	. . . . . . . . . . . . 13 |- F/ r w = 0
41		dfsbcq2 2818	. . . . . . . . . . . . . 14 |- ( w = 0 -> ( [ w / x ] ps <-> [. 0 / x ]. ps ) )
42		bezout.sub-gcd	. . . . . . . . . . . . . . . 16 |- ( ps <-> A. z e. NN0 ( z || r -> ( z || x /\ z || y ) ) )
43	42	sbcbii 2873	. . . . . . . . . . . . . . 15 |- ( [. 0 / x ]. ps <-> [. 0 / x ]. A. z e. NN0 ( z || r -> ( z || x /\ z || y ) ) )
44		c0ex 7113	. . . . . . . . . . . . . . . 16 |- 0 e. _V
45		breq2 3789	. . . . . . . . . . . . . . . . . . 19 |- ( x = 0 -> ( z || x <-> z || 0 ) )
46	45	anbi1d 452	. . . . . . . . . . . . . . . . . 18 |- ( x = 0 -> ( ( z || x /\ z || y ) <-> ( z || 0 /\ z || y ) ) )
47	46	imbi2d 228	. . . . . . . . . . . . . . . . 17 |- ( x = 0 -> ( ( z || r -> ( z || x /\ z || y ) ) <-> ( z || r -> ( z || 0 /\ z || y ) ) ) )
48	47	ralbidv 2368	. . . . . . . . . . . . . . . 16 |- ( x = 0 -> ( A. z e. NN0 ( z || r -> ( z || x /\ z || y ) ) <-> A. z e. NN0 ( z || r -> ( z || 0 /\ z || y ) ) ) )
49	44, 48	sbcie 2848	. . . . . . . . . . . . . . 15 |- ( [. 0 / x ]. A. z e. NN0 ( z || r -> ( z || x /\ z || y ) ) <-> A. z e. NN0 ( z || r -> ( z || 0 /\ z || y ) ) )
50	43, 49	bitri 182	. . . . . . . . . . . . . 14 |- ( [. 0 / x ]. ps <-> A. z e. NN0 ( z || r -> ( z || 0 /\ z || y ) ) )
51	41, 50	syl6bb 194	. . . . . . . . . . . . 13 |- ( w = 0 -> ( [ w / x ] ps <-> A. z e. NN0 ( z || r -> ( z || 0 /\ z || y ) ) ) )
52	40, 51	sbbid 1767	. . . . . . . . . . . 12 |- ( w = 0 -> ( [ y / r ] [ w / x ] ps <-> [ y / r ] A. z e. NN0 ( z || r -> ( z || 0 /\ z || y ) ) ) )
53	39, 52	mpbiri 166	. . . . . . . . . . 11 |- ( w = 0 -> [ y / r ] [ w / x ] ps )
54	53	ad3antlr 476	. . . . . . . . . 10 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ w = 0 ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> [ y / r ] [ w / x ] ps )
55		simpr 108	. . . . . . . . . 10 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ w = 0 ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> [ y / r ] ph )
56		nfs1v 1856	. . . . . . . . . . . 12 |- F/ r [ y / r ] [ w / x ] ps
57		nfs1v 1856	. . . . . . . . . . . 12 |- F/ r [ y / r ] ph
58	56, 57	nfan 1497	. . . . . . . . . . 11 |- F/ r ( [ y / r ] [ w / x ] ps /\ [ y / r ] ph )
59		sbequ12 1694	. . . . . . . . . . . 12 |- ( r = y -> ( [ w / x ] ps <-> [ y / r ] [ w / x ] ps ) )
60		sbequ12 1694	. . . . . . . . . . . 12 |- ( r = y -> ( ph <-> [ y / r ] ph ) )
61	59, 60	anbi12d 456	. . . . . . . . . . 11 |- ( r = y -> ( ( [ w / x ] ps /\ ph ) <-> ( [ y / r ] [ w / x ] ps /\ [ y / r ] ph ) ) )
62	58, 61	rspce 2696	. . . . . . . . . 10 |- ( ( y e. NN0 /\ ( [ y / r ] [ w / x ] ps /\ [ y / r ] ph ) ) -> E. r e. NN0 ( [ w / x ] ps /\ ph ) )
63	28, 54, 55, 62	syl12anc 1167	. . . . . . . . 9 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ w = 0 ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> E. r e. NN0 ( [ w / x ] ps /\ ph ) )
64	63	exp31 356	. . . . . . . 8 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ w = 0 ) -> ( y e. NN0 -> ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) ) )
65	27, 64	ralrimi 2432	. . . . . . 7 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ w = 0 ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) )
66		nfv 1461	. . . . . . . . . 10 |- F/ y 0 < w
67	25, 66	nfan 1497	. . . . . . . . 9 |- F/ y ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w )
68		bezout.is-bezout	. . . . . . . . . . 11 |- ( ph <-> E. s e. ZZ E. t e. ZZ r = ( ( A x. s ) + ( B x. t ) ) )
69		simplrl 501	. . . . . . . . . . . . 13 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> th )
70		bezout.a	. . . . . . . . . . . . 13 |- ( th -> A e. NN0 )
71	69, 70	syl 14	. . . . . . . . . . . 12 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> A e. NN0 )
72	71	ad2antrr 471	. . . . . . . . . . 11 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> A e. NN0 )
73		bezout.b	. . . . . . . . . . . . 13 |- ( th -> B e. NN0 )
74	69, 73	syl 14	. . . . . . . . . . . 12 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> B e. NN0 )
75	74	ad2antrr 471	. . . . . . . . . . 11 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> B e. NN0 )
76		simplll 499	. . . . . . . . . . . . 13 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> w e. NN0 )
77		simpr 108	. . . . . . . . . . . . 13 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> 0 < w )
78		elnnnn0b 8332	. . . . . . . . . . . . 13 |- ( w e. NN <-> ( w e. NN0 /\ 0 < w ) )
79	76, 77, 78	sylanbrc 408	. . . . . . . . . . . 12 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> w e. NN )
80	79	ad2antrr 471	. . . . . . . . . . 11 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> w e. NN )
81		simpr 108	. . . . . . . . . . 11 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> [ y / r ] ph )
82		simplr 496	. . . . . . . . . . 11 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> y e. NN0 )
83		simplrr 502	. . . . . . . . . . . . 13 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> [ w / r ] ph )
84		sbsbc 2819	. . . . . . . . . . . . 13 |- ( [ w / r ] ph <-> [. w / r ]. ph )
85	83, 84	sylib 120	. . . . . . . . . . . 12 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> [. w / r ]. ph )
86	85	ad2antrr 471	. . . . . . . . . . 11 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> [. w / r ]. ph )
87		breq1 3788	. . . . . . . . . . . . . 14 |- ( z = a -> ( z || r <-> a || r ) )
88		breq1 3788	. . . . . . . . . . . . . . 15 |- ( z = a -> ( z || x <-> a || x ) )
89		breq1 3788	. . . . . . . . . . . . . . 15 |- ( z = a -> ( z || y <-> a || y ) )
90	88, 89	anbi12d 456	. . . . . . . . . . . . . 14 |- ( z = a -> ( ( z || x /\ z || y ) <-> ( a || x /\ a || y ) ) )
91	87, 90	imbi12d 232	. . . . . . . . . . . . 13 |- ( z = a -> ( ( z || r -> ( z || x /\ z || y ) ) <-> ( a || r -> ( a || x /\ a || y ) ) ) )
92	91	cbvralv 2577	. . . . . . . . . . . 12 |- ( A. z e. NN0 ( z || r -> ( z || x /\ z || y ) ) <-> A. a e. NN0 ( a || r -> ( a || x /\ a || y ) ) )
93	42, 92	bitri 182	. . . . . . . . . . 11 |- ( ps <-> A. a e. NN0 ( a || r -> ( a || x /\ a || y ) ) )
94	69	ad3antrrr 475	. . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> th )
95		simpr 108	. . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> [. ( y mod w ) / r ]. ph )
96	94, 95	jca 300	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> ( th /\ [. ( y mod w ) / r ]. ph ) )
97	83	ad3antrrr 475	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> [ w / r ] ph )
98		simpllr 500	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> y e. NN0 )
99	98	nn0zd 8467	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> y e. ZZ )
100	79	ad3antrrr 475	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> w e. NN )
101		zmodfz 9348	. . . . . . . . . . . . . 14 |- ( ( y e. ZZ /\ w e. NN ) -> ( y mod w ) e. ( 0 ... ( w - 1 ) ) )
102	99, 100, 101	syl2anc 403	. . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> ( y mod w ) e. ( 0 ... ( w - 1 ) ) )
103		simpll 495	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) )
104		simpr 108	. . . . . . . . . . . . . . . 16 |- ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) -> A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) )
105	104	ad3antrrr 475	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ [. ( y mod w ) / r ]. ph ) -> A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) )
106		nfv 1461	. . . . . . . . . . . . . . . . . . . 20 |- F/ y [ w / r ] ph
107		nfcv 2219	. . . . . . . . . . . . . . . . . . . . 21 |- F/_ y NN0
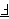108		nfs1v 1856	. . . . . . . . . . . . . . . . . . . . . . 23 |- F/ y [ w / y ] ps
109	108	nfsbxy 1859	. . . . . . . . . . . . . . . . . . . . . 22 |- F/ y [ z / x ] [ w / y ] ps
110		nfv 1461	. . . . . . . . . . . . . . . . . . . . . 22 |- F/ y ph
111	109, 110	nfan 1497	. . . . . . . . . . . . . . . . . . . . 21 |- F/ y ( [ z / x ] [ w / y ] ps /\ ph )
112	107, 111	nfrexxy 2403	. . . . . . . . . . . . . . . . . . . 20 |- F/ y E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph )
113	106, 112	nfim 1504	. . . . . . . . . . . . . . . . . . 19 |- F/ y ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) )
114		sbequ 1761	. . . . . . . . . . . . . . . . . . . 20 |- ( y = w -> ( [ y / r ] ph <-> [ w / r ] ph ) )
115		nfv 1461	. . . . . . . . . . . . . . . . . . . . . . 23 |- F/ x y = w
116		sbequ12 1694	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( y = w -> ( ps <-> [ w / y ] ps ) )
117	115, 116	sbbid 1767	. . . . . . . . . . . . . . . . . . . . . 22 |- ( y = w -> ( [ z / x ] ps <-> [ z / x ] [ w / y ] ps ) )
118	117	anbi1d 452	. . . . . . . . . . . . . . . . . . . . 21 |- ( y = w -> ( ( [ z / x ] ps /\ ph ) <-> ( [ z / x ] [ w / y ] ps /\ ph ) ) )
119	118	rexbidv 2369	. . . . . . . . . . . . . . . . . . . 20 |- ( y = w -> ( E. r e. NN0 ( [ z / x ] ps /\ ph ) <-> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) )
120	114, 119	imbi12d 232	. . . . . . . . . . . . . . . . . . 19 |- ( y = w -> ( ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) <-> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) )
121	113, 120	rspc 2695	. . . . . . . . . . . . . . . . . 18 |- ( w e. NN0 -> ( A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) -> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) )
122	121	imim2d 53	. . . . . . . . . . . . . . . . 17 |- ( w e. NN0 -> ( ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) -> ( ( th /\ [ z / r ] ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) ) )
123	122	ralimdv 2430	. . . . . . . . . . . . . . . 16 |- ( w e. NN0 -> ( A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) -> A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) ) )
124	123	ad4antr 477	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ [. ( y mod w ) / r ]. ph ) -> ( A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) -> A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) ) )
125	105, 124	mpd 13	. . . . . . . . . . . . . 14 |- ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ [. ( y mod w ) / r ]. ph ) -> A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) )
126	103, 125	sylan 277	. . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) )
127		dfsbcq2 2818	. . . . . . . . . . . . . . . 16 |- ( z = ( y mod w ) -> ( [ z / r ] ph <-> [. ( y mod w ) / r ]. ph ) )
128	127	anbi2d 451	. . . . . . . . . . . . . . 15 |- ( z = ( y mod w ) -> ( ( th /\ [ z / r ] ph ) <-> ( th /\ [. ( y mod w ) / r ]. ph ) ) )
129		sbsbc 2819	. . . . . . . . . . . . . . . . . . . 20 |- ( [ z / x ] [ w / y ] ps <-> [. z / x ]. [ w / y ] ps )
130		sbsbc 2819	. . . . . . . . . . . . . . . . . . . . 21 |- ( [ w / y ] ps <-> [. w / y ]. ps )
131	130	sbcbii 2873	. . . . . . . . . . . . . . . . . . . 20 |- ( [. z / x ]. [ w / y ] ps <-> [. z / x ]. [. w / y ]. ps )
132	129, 131	bitri 182	. . . . . . . . . . . . . . . . . . 19 |- ( [ z / x ] [ w / y ] ps <-> [. z / x ]. [. w / y ]. ps )
133	132	anbi1i 445	. . . . . . . . . . . . . . . . . 18 |- ( ( [ z / x ] [ w / y ] ps /\ ph ) <-> ( [. z / x ]. [. w / y ]. ps /\ ph ) )
134		dfsbcq 2817	. . . . . . . . . . . . . . . . . . 19 |- ( z = ( y mod w ) -> ( [. z / x ]. [. w / y ]. ps <-> [. ( y mod w ) / x ]. [. w / y ]. ps ) )
135	134	anbi1d 452	. . . . . . . . . . . . . . . . . 18 |- ( z = ( y mod w ) -> ( ( [. z / x ]. [. w / y ]. ps /\ ph ) <-> ( [. ( y mod w ) / x ]. [. w / y ]. ps /\ ph ) ) )
136	133, 135	syl5bb 190	. . . . . . . . . . . . . . . . 17 |- ( z = ( y mod w ) -> ( ( [ z / x ] [ w / y ] ps /\ ph ) <-> ( [. ( y mod w ) / x ]. [. w / y ]. ps /\ ph ) ) )
137	136	rexbidv 2369	. . . . . . . . . . . . . . . 16 |- ( z = ( y mod w ) -> ( E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) <-> E. r e. NN0 ( [. ( y mod w ) / x ]. [. w / y ]. ps /\ ph ) ) )
138	137	imbi2d 228	. . . . . . . . . . . . . . 15 |- ( z = ( y mod w ) -> ( ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) <-> ( [ w / r ] ph -> E. r e. NN0 ( [. ( y mod w ) / x ]. [. w / y ]. ps /\ ph ) ) ) )
139	128, 138	imbi12d 232	. . . . . . . . . . . . . 14 |- ( z = ( y mod w ) -> ( ( ( th /\ [ z / r ] ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) <-> ( ( th /\ [. ( y mod w ) / r ]. ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [. ( y mod w ) / x ]. [. w / y ]. ps /\ ph ) ) ) ) )
140	139	rspcv 2697	. . . . . . . . . . . . 13 |- ( ( y mod w ) e. ( 0 ... ( w - 1 ) ) -> ( A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [ z / x ] [ w / y ] ps /\ ph ) ) ) -> ( ( th /\ [. ( y mod w ) / r ]. ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [. ( y mod w ) / x ]. [. w / y ]. ps /\ ph ) ) ) ) )
141	102, 126, 140	sylc 61	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> ( ( th /\ [. ( y mod w ) / r ]. ph ) -> ( [ w / r ] ph -> E. r e. NN0 ( [. ( y mod w ) / x ]. [. w / y ]. ps /\ ph ) ) ) )
142	96, 97, 141	mp2d 46	. . . . . . . . . . 11 |- ( ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) /\ [. ( y mod w ) / r ]. ph ) -> E. r e. NN0 ( [. ( y mod w ) / x ]. [. w / y ]. ps /\ ph ) )
143		nfv 1461	. . . . . . . . . . . . . . . 16 |- F/ x w e. NN0
144		nfcv 2219	. . . . . . . . . . . . . . . . 17 |- F/_ x ( 0 ... ( w - 1 ) )
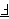145		nfv 1461	. . . . . . . . . . . . . . . . . 18 |- F/ x ( th /\ [ z / r ] ph )
146		nfcv 2219	. . . . . . . . . . . . . . . . . . 19 |- F/_ x NN0
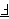147		nfv 1461	. . . . . . . . . . . . . . . . . . . . 21 |- F/ x ph
148	147	nfsbxy 1859	. . . . . . . . . . . . . . . . . . . 20 |- F/ x [ y / r ] ph
149		nfs1v 1856	. . . . . . . . . . . . . . . . . . . . . 22 |- F/ x [ z / x ] ps
150	149, 147	nfan 1497	. . . . . . . . . . . . . . . . . . . . 21 |- F/ x ( [ z / x ] ps /\ ph )
151	146, 150	nfrexxy 2403	. . . . . . . . . . . . . . . . . . . 20 |- F/ x E. r e. NN0 ( [ z / x ] ps /\ ph )
152	148, 151	nfim 1504	. . . . . . . . . . . . . . . . . . 19 |- F/ x ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) )
153	146, 152	nfralxy 2402	. . . . . . . . . . . . . . . . . 18 |- F/ x A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) )
154	145, 153	nfim 1504	. . . . . . . . . . . . . . . . 17 |- F/ x ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) )
155	144, 154	nfralxy 2402	. . . . . . . . . . . . . . . 16 |- F/ x A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) )
156	143, 155	nfan 1497	. . . . . . . . . . . . . . 15 |- F/ x ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) )
157		nfv 1461	. . . . . . . . . . . . . . 15 |- F/ x ( th /\ [ w / r ] ph )
158	156, 157	nfan 1497	. . . . . . . . . . . . . 14 |- F/ x ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) )
159		nfv 1461	. . . . . . . . . . . . . 14 |- F/ x 0 < w
160	158, 159	nfan 1497	. . . . . . . . . . . . 13 |- F/ x ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w )
161		nfv 1461	. . . . . . . . . . . . 13 |- F/ x y e. NN0
162	160, 161	nfan 1497	. . . . . . . . . . . 12 |- F/ x ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 )
163	162, 148	nfan 1497	. . . . . . . . . . 11 |- F/ x ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph )
164		nfv 1461	. . . . . . . . . . . . . . . 16 |- F/ r w e. NN0
165		nfcv 2219	. . . . . . . . . . . . . . . . 17 |- F/_ r ( 0 ... ( w - 1 ) )
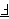166		nfv 1461	. . . . . . . . . . . . . . . . . . 19 |- F/ r th
167		nfs1v 1856	. . . . . . . . . . . . . . . . . . 19 |- F/ r [ z / r ] ph
168	166, 167	nfan 1497	. . . . . . . . . . . . . . . . . 18 |- F/ r ( th /\ [ z / r ] ph )
169		nfcv 2219	. . . . . . . . . . . . . . . . . . 19 |- F/_ r NN0
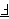170		nfre1 2407	. . . . . . . . . . . . . . . . . . . 20 |- F/ r E. r e. NN0 ( [ z / x ] ps /\ ph )
171	57, 170	nfim 1504	. . . . . . . . . . . . . . . . . . 19 |- F/ r ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) )
172	169, 171	nfralxy 2402	. . . . . . . . . . . . . . . . . 18 |- F/ r A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) )
173	168, 172	nfim 1504	. . . . . . . . . . . . . . . . 17 |- F/ r ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) )
174	165, 173	nfralxy 2402	. . . . . . . . . . . . . . . 16 |- F/ r A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) )
175	164, 174	nfan 1497	. . . . . . . . . . . . . . 15 |- F/ r ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) )
176		nfs1v 1856	. . . . . . . . . . . . . . . 16 |- F/ r [ w / r ] ph
177	166, 176	nfan 1497	. . . . . . . . . . . . . . 15 |- F/ r ( th /\ [ w / r ] ph )
178	175, 177	nfan 1497	. . . . . . . . . . . . . 14 |- F/ r ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) )
179		nfv 1461	. . . . . . . . . . . . . 14 |- F/ r 0 < w
180	178, 179	nfan 1497	. . . . . . . . . . . . 13 |- F/ r ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w )
181		nfv 1461	. . . . . . . . . . . . 13 |- F/ r y e. NN0
182	180, 181	nfan 1497	. . . . . . . . . . . 12 |- F/ r ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 )
183	182, 57	nfan 1497	. . . . . . . . . . 11 |- F/ r ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph )
184	68, 72, 75, 80, 81, 82, 86, 93, 142, 163, 183	bezoutlemstep 10386	. . . . . . . . . 10 |- ( ( ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) /\ y e. NN0 ) /\ [ y / r ] ph ) -> E. r e. NN0 ( [. w / x ]. ps /\ ph ) )
185	184	exp31 356	. . . . . . . . 9 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> ( y e. NN0 -> ( [ y / r ] ph -> E. r e. NN0 ( [. w / x ]. ps /\ ph ) ) ) )
186	67, 185	ralrimi 2432	. . . . . . . 8 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [. w / x ]. ps /\ ph ) ) )
187		sbsbc 2819	. . . . . . . . . . . 12 |- ( [ w / x ] ps <-> [. w / x ]. ps )
188	187	anbi1i 445	. . . . . . . . . . 11 |- ( ( [ w / x ] ps /\ ph ) <-> ( [. w / x ]. ps /\ ph ) )
189	188	rexbii 2373	. . . . . . . . . 10 |- ( E. r e. NN0 ( [ w / x ] ps /\ ph ) <-> E. r e. NN0 ( [. w / x ]. ps /\ ph ) )
190	189	imbi2i 224	. . . . . . . . 9 |- ( ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) <-> ( [ y / r ] ph -> E. r e. NN0 ( [. w / x ]. ps /\ ph ) ) )
191	190	ralbii 2372	. . . . . . . 8 |- ( A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) <-> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [. w / x ]. ps /\ ph ) ) )
192	186, 191	sylibr 132	. . . . . . 7 |- ( ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) /\ 0 < w ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) )
193		nn0nlt0 8314	. . . . . . . . 9 |- ( w e. NN0 -> -. w < 0 )
194		nn0z 8371	. . . . . . . . . . . 12 |- ( w e. NN0 -> w e. ZZ )
195		ztri3or0 8393	. . . . . . . . . . . 12 |- ( w e. ZZ -> ( w < 0 \/ w = 0 \/ 0 < w ) )
196	194, 195	syl 14	. . . . . . . . . . 11 |- ( w e. NN0 -> ( w < 0 \/ w = 0 \/ 0 < w ) )
197		3orass 922	. . . . . . . . . . 11 |- ( ( w < 0 \/ w = 0 \/ 0 < w ) <-> ( w < 0 \/ ( w = 0 \/ 0 < w ) ) )
198	196, 197	sylib 120	. . . . . . . . . 10 |- ( w e. NN0 -> ( w < 0 \/ ( w = 0 \/ 0 < w ) ) )
199	198	orcomd 680	. . . . . . . . 9 |- ( w e. NN0 -> ( ( w = 0 \/ 0 < w ) \/ w < 0 ) )
200	193, 199	ecased 1280	. . . . . . . 8 |- ( w e. NN0 -> ( w = 0 \/ 0 < w ) )
201	200	ad2antrr 471	. . . . . . 7 |- ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) -> ( w = 0 \/ 0 < w ) )
202	65, 192, 201	mpjaodan 744	. . . . . 6 |- ( ( ( w e. NN0 /\ A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) ) /\ ( th /\ [ w / r ] ph ) ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) )
203	202	exp31 356	. . . . 5 |- ( w e. NN0 -> ( A. z e. ( 0 ... ( w - 1 ) ) ( ( th /\ [ z / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ z / x ] ps /\ ph ) ) ) -> ( ( th /\ [ w / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( [ w / x ] ps /\ ph ) ) ) ) )
204	8, 16, 203	nn0sinds 9430	. . . 4 |- ( x e. NN0 -> ( ( th /\ [ x / r ] ph ) -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( ps /\ ph ) ) ) )
205	204	expd 254	. . 3 |- ( x e. NN0 -> ( th -> ( [ x / r ] ph -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( ps /\ ph ) ) ) ) )
206	205	impcom 123	. 2 |- ( ( th /\ x e. NN0 ) -> ( [ x / r ] ph -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( ps /\ ph ) ) ) )
207	206	ralrimiva 2434	1 |- ( th -> A. x e. NN0 ( [ x / r ] ph -> A. y e. NN0 ( [ y / r ] ph -> E. r e. NN0 ( ps /\ ph ) ) ) )

Syntax hints:   -> wi 4   /\ wa 102   <-> wb 103   \/ wo 661   \/ w3o 918   = wceq 1284   e. wcel 1433   [wsb 1685   A.wral 2348   E.wrex 2349   [.wsbc 2815   class class class wbr 3785  (class class class)co 5532   0cc0 6981   1c1 6982   + caddc 6984   x. cmul 6986   < clt 7153   - cmin 7279   NNcn 8039   NN0cn0 8288   ZZcz 8351   ...cfz 9029   mod cmo 9324   || cdvds 10195

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 104  ax-ia2 105  ax-ia3 106  ax-in1 576  ax-in2 577  ax-io 662  ax-5 1376  ax-7 1377  ax-gen 1378  ax-ie1 1422  ax-ie2 1423  ax-8 1435  ax-10 1436  ax-11 1437  ax-i12 1438  ax-bndl 1439  ax-4 1440  ax-13 1444  ax-14 1445  ax-17 1459  ax-i9 1463  ax-ial 1467  ax-i5r 1468  ax-ext 2063  ax-coll 3893  ax-sep 3896  ax-nul 3904  ax-pow 3948  ax-pr 3964  ax-un 4188  ax-setind 4280  ax-iinf 4329  ax-cnex 7067  ax-resscn 7068  ax-1cn 7069  ax-1re 7070  ax-icn 7071  ax-addcl 7072  ax-addrcl 7073  ax-mulcl 7074  ax-mulrcl 7075  ax-addcom 7076  ax-mulcom 7077  ax-addass 7078  ax-mulass 7079  ax-distr 7080  ax-i2m1 7081  ax-0lt1 7082  ax-1rid 7083  ax-0id 7084  ax-rnegex 7085  ax-precex 7086  ax-cnre 7087  ax-pre-ltirr 7088  ax-pre-ltwlin 7089  ax-pre-lttrn 7090  ax-pre-apti 7091  ax-pre-ltadd 7092  ax-pre-mulgt0 7093  ax-pre-mulext 7094  ax-arch 7095

This theorem depends on definitions:  df-bi 115  df-dc 776  df-3or 920  df-3an 921  df-tru 1287  df-fal 1290  df-nf 1390  df-sb 1686  df-eu 1944  df-mo 1945  df-clab 2068  df-cleq 2074  df-clel 2077  df-nfc 2208  df-ne 2246  df-nel 2340  df-ral 2353  df-rex 2354  df-reu 2355  df-rmo 2356  df-rab 2357  df-v 2603  df-sbc 2816  df-csb 2909  df-dif 2975  df-un 2977  df-in 2979  df-ss 2986  df-nul 3252  df-if 3352  df-pw 3384  df-sn 3404  df-pr 3405  df-op 3407  df-uni 3602  df-int 3637  df-iun 3680  df-br 3786  df-opab 3840  df-mpt 3841  df-tr 3876  df-id 4048  df-po 4051  df-iso 4052  df-iord 4121  df-on 4123  df-suc 4126  df-iom 4332  df-xp 4369  df-rel 4370  df-cnv 4371  df-co 4372  df-dm 4373  df-rn 4374  df-res 4375  df-ima 4376  df-iota 4887  df-fun 4924  df-fn 4925  df-f 4926  df-f1 4927  df-fo 4928  df-f1o 4929  df-fv 4930  df-riota 5488  df-ov 5535  df-oprab 5536  df-mpt2 5537  df-1st 5787  df-2nd 5788  df-recs 5943  df-frec 6001  df-pnf 7155  df-mnf 7156  df-xr 7157  df-ltxr 7158  df-le 7159  df-sub 7281  df-neg 7282  df-reap 7675  df-ap 7682  df-div 7761  df-inn 8040  df-2 8098  df-n0 8289  df-z 8352  df-uz 8620  df-q 8705  df-rp 8735  df-fz 9030  df-fl 9274  df-mod 9325  df-iseq 9432  df-iexp 9476  df-cj 9729  df-re 9730  df-im 9731  df-rsqrt 9884  df-abs 9885  df-dvds 10196

This theorem is referenced by:  bezoutlemex  10390