Users' Mathboxes Mathbox for Norm Megill < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  MPE Home  >  Th. List  >   Mathboxes  >  ltrneq2 Structured version   Visualization version   Unicode version
Theorem ltrneq2 35434
Description: The equality of two translations is determined by their equality at atoms. (Contributed by NM, 2-Mar-2014.)
Hypotheses
Ref Expression
ltrneq2.a |- A = ( Atoms ` K )
ltrneq2.h |- H = ( LHyp ` K )
ltrneq2.t |- T = ( ( LTrn ` K ) ` W )
Assertion
Ref Expression
ltrneq2 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( A. p e. A ( F ` p ) = ( G ` p ) <-> F = G ) )
Distinct variable groups:   A, p   F, p   G, p
Allowed substitution hints:   T( p)   H( p)   K( p)   W( p)
Proof of Theorem ltrneq2
Dummy variables q x are mutually distinct and distinct from all other variables.
StepHypRef Expression
1 simpl1 1064 . . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( K e. HL /\ W e. H ) )
2 simpl3 1066 . . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> G e. T )
3 eqid 2622 . . . . . . . . . . . . . . 15 |- ( Base ` K ) = ( Base ` K )
4 ltrneq2.h . . . . . . . . . . . . . . 15 |- H = ( LHyp ` K )
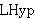5 ltrneq2.t . . . . . . . . . . . . . . 15 |- T = ( ( LTrn ` K ) ` W )
63, 4, 5ltrn1o 35410 . . . . . . . . . . . . . 14 |- ( ( ( K e. HL /\ W e. H ) /\ G e. T ) -> G : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
71, 2, 6syl2anc 693 . . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> G : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
8 simpl2 1065 . . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> F e. T )
9 simpr3 1069 . . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> q e. A )
10 eqid 2622 . . . . . . . . . . . . . . . 16 |- ( le ` K ) = ( le ` K )
11 ltrneq2.a . . . . . . . . . . . . . . . 16 |- A = ( Atoms ` K )
1210, 11, 4, 5ltrncnvat 35427 . . . . . . . . . . . . . . 15 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ q e. A ) -> ( `' F ` q ) e. A )
131, 8, 9, 12syl3anc 1326 . . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( `' F ` q ) e. A )
143, 11atbase 34576 . . . . . . . . . . . . . 14 |- ( ( `' F ` q ) e. A -> ( `' F ` q ) e. ( Base ` K ) )
1513, 14syl 17 . . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( `' F ` q ) e. ( Base ` K ) )
16 f1ocnvfv1 6532 . . . . . . . . . . . . 13 |- ( ( G : ( Base ` K ) -1-1-onto-> ( Base ` K ) /\ ( `' F ` q ) e. ( Base ` K ) ) -> ( `' G ` ( G ` ( `' F ` q ) ) ) = ( `' F ` q ) )
177, 15, 16syl2anc 693 . . . . . . . . . . . 12 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( `' G ` ( G ` ( `' F ` q ) ) ) = ( `' F ` q ) )
18 simpr2 1068 . . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> A. p e. A ( F ` p ) = ( G ` p ) )
19 fveq2 6191 . . . . . . . . . . . . . . . . 17 |- ( p = ( `' F ` q ) -> ( F ` p ) = ( F ` ( `' F ` q ) ) )
20 fveq2 6191 . . . . . . . . . . . . . . . . 17 |- ( p = ( `' F ` q ) -> ( G ` p ) = ( G ` ( `' F ` q ) ) )
2119, 20eqeq12d 2637 . . . . . . . . . . . . . . . 16 |- ( p = ( `' F ` q ) -> ( ( F ` p ) = ( G ` p ) <-> ( F ` ( `' F ` q ) ) = ( G ` ( `' F ` q ) ) ) )
2221rspcv 3305 . . . . . . . . . . . . . . 15 |- ( ( `' F ` q ) e. A -> ( A. p e. A ( F ` p ) = ( G ` p ) -> ( F ` ( `' F ` q ) ) = ( G ` ( `' F ` q ) ) ) )
2313, 18, 22sylc 65 . . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( F ` ( `' F ` q ) ) = ( G ` ( `' F ` q ) ) )
243, 4, 5ltrn1o 35410 . . . . . . . . . . . . . . . 16 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T ) -> F : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
251, 8, 24syl2anc 693 . . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> F : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
263, 11atbase 34576 . . . . . . . . . . . . . . . 16 |- ( q e. A -> q e. ( Base ` K ) )
279, 26syl 17 . . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> q e. ( Base ` K ) )
28 f1ocnvfv2 6533 . . . . . . . . . . . . . . 15 |- ( ( F : ( Base ` K ) -1-1-onto-> ( Base ` K ) /\ q e. ( Base ` K ) ) -> ( F ` ( `' F ` q ) ) = q )
2925, 27, 28syl2anc 693 . . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( F ` ( `' F ` q ) ) = q )
3023, 29eqtr3d 2658 . . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( G ` ( `' F ` q ) ) = q )
3130fveq2d 6195 . . . . . . . . . . . 12 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( `' G ` ( G ` ( `' F ` q ) ) ) = ( `' G ` q ) )
3217, 31eqtr3d 2658 . . . . . . . . . . 11 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( `' F ` q ) = ( `' G ` q ) )
3332breq1d 4663 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( ( `' F ` q ) ( le ` K ) x <-> ( `' G ` q ) ( le ` K ) x ) )
34 simpr1 1067 . . . . . . . . . . . 12 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> x e. ( Base ` K ) )
35 f1ocnvfv1 6532 . . . . . . . . . . . 12 |- ( ( F : ( Base ` K ) -1-1-onto-> ( Base ` K ) /\ x e. ( Base ` K ) ) -> ( `' F ` ( F ` x ) ) = x )
3625, 34, 35syl2anc 693 . . . . . . . . . . 11 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( `' F ` ( F ` x ) ) = x )
3736breq2d 4665 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( ( `' F ` q ) ( le ` K ) ( `' F ` ( F ` x ) ) <-> ( `' F ` q ) ( le ` K ) x ) )
38 f1ocnvfv1 6532 . . . . . . . . . . . 12 |- ( ( G : ( Base ` K ) -1-1-onto-> ( Base ` K ) /\ x e. ( Base ` K ) ) -> ( `' G ` ( G ` x ) ) = x )
397, 34, 38syl2anc 693 . . . . . . . . . . 11 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( `' G ` ( G ` x ) ) = x )
4039breq2d 4665 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( ( `' G ` q ) ( le ` K ) ( `' G ` ( G ` x ) ) <-> ( `' G ` q ) ( le ` K ) x ) )
4133, 37, 403bitr4d 300 . . . . . . . . 9 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( ( `' F ` q ) ( le ` K ) ( `' F ` ( F ` x ) ) <-> ( `' G ` q ) ( le ` K ) ( `' G ` ( G ` x ) ) ) )
42 simpl1l 1112 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> K e. HL )
43 eqid 2622 . . . . . . . . . . . 12 |- ( LAut ` K ) = ( LAut ` K )
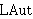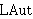444, 43, 5ltrnlaut 35409 . . . . . . . . . . 11 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T ) -> F e. ( LAut ` K ) )
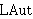451, 8, 44syl2anc 693 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> F e. ( LAut ` K ) )
463, 4, 5ltrncl 35411 . . . . . . . . . . 11 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ x e. ( Base ` K ) ) -> ( F ` x ) e. ( Base ` K ) )
471, 8, 34, 46syl3anc 1326 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( F ` x ) e. ( Base ` K ) )
483, 10, 43lautcnvle 35375 . . . . . . . . . 10 |- ( ( ( K e. HL /\ F e. ( LAut ` K ) ) /\ ( q e. ( Base ` K ) /\ ( F ` x ) e. ( Base ` K ) ) ) -> ( q ( le ` K ) ( F ` x ) <-> ( `' F ` q ) ( le ` K ) ( `' F ` ( F ` x ) ) ) )
4942, 45, 27, 47, 48syl22anc 1327 . . . . . . . . 9 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( q ( le ` K ) ( F ` x ) <-> ( `' F ` q ) ( le ` K ) ( `' F ` ( F ` x ) ) ) )
504, 43, 5ltrnlaut 35409 . . . . . . . . . . 11 |- ( ( ( K e. HL /\ W e. H ) /\ G e. T ) -> G e. ( LAut ` K ) )
511, 2, 50syl2anc 693 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> G e. ( LAut ` K ) )
523, 4, 5ltrncl 35411 . . . . . . . . . . 11 |- ( ( ( K e. HL /\ W e. H ) /\ G e. T /\ x e. ( Base ` K ) ) -> ( G ` x ) e. ( Base ` K ) )
531, 2, 34, 52syl3anc 1326 . . . . . . . . . 10 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( G ` x ) e. ( Base ` K ) )
543, 10, 43lautcnvle 35375 . . . . . . . . . 10 |- ( ( ( K e. HL /\ G e. ( LAut ` K ) ) /\ ( q e. ( Base ` K ) /\ ( G ` x ) e. ( Base ` K ) ) ) -> ( q ( le ` K ) ( G ` x ) <-> ( `' G ` q ) ( le ` K ) ( `' G ` ( G ` x ) ) ) )
5542, 51, 27, 53, 54syl22anc 1327 . . . . . . . . 9 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( q ( le ` K ) ( G ` x ) <-> ( `' G ` q ) ( le ` K ) ( `' G ` ( G ` x ) ) ) )
5641, 49, 553bitr4d 300 . . . . . . . 8 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( x e. ( Base ` K ) /\ A. p e. A ( F ` p ) = ( G ` p ) /\ q e. A ) ) -> ( q ( le ` K ) ( F ` x ) <-> q ( le ` K ) ( G ` x ) ) )
57563exp2 1285 . . . . . . 7 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( x e. ( Base ` K ) -> ( A. p e. A ( F ` p ) = ( G ` p ) -> ( q e. A -> ( q ( le ` K ) ( F ` x ) <-> q ( le ` K ) ( G ` x ) ) ) ) ) )
5857imp 445 . . . . . 6 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> ( A. p e. A ( F ` p ) = ( G ` p ) -> ( q e. A -> ( q ( le ` K ) ( F ` x ) <-> q ( le ` K ) ( G ` x ) ) ) ) )
5958ralrimdv 2968 . . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> ( A. p e. A ( F ` p ) = ( G ` p ) -> A. q e. A ( q ( le ` K ) ( F ` x ) <-> q ( le ` K ) ( G ` x ) ) ) )
60 simpl1l 1112 . . . . . 6 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> K e. HL )
61 simpl1 1064 . . . . . . 7 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> ( K e. HL /\ W e. H ) )
62 simpl2 1065 . . . . . . 7 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> F e. T )
63 simpr 477 . . . . . . 7 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> x e. ( Base ` K ) )
6461, 62, 63, 46syl3anc 1326 . . . . . 6 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> ( F ` x ) e. ( Base ` K ) )
65 simpl3 1066 . . . . . . 7 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> G e. T )
6661, 65, 63, 52syl3anc 1326 . . . . . 6 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> ( G ` x ) e. ( Base ` K ) )
673, 10, 11hlateq 34685 . . . . . 6 |- ( ( K e. HL /\ ( F ` x ) e. ( Base ` K ) /\ ( G ` x ) e. ( Base ` K ) ) -> ( A. q e. A ( q ( le ` K ) ( F ` x ) <-> q ( le ` K ) ( G ` x ) ) <-> ( F ` x ) = ( G ` x ) ) )
6860, 64, 66, 67syl3anc 1326 . . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> ( A. q e. A ( q ( le ` K ) ( F ` x ) <-> q ( le ` K ) ( G ` x ) ) <-> ( F ` x ) = ( G ` x ) ) )
6959, 68sylibd 229 . . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ x e. ( Base ` K ) ) -> ( A. p e. A ( F ` p ) = ( G ` p ) -> ( F ` x ) = ( G ` x ) ) )
7069ralrimdva 2969 . . 3 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( A. p e. A ( F ` p ) = ( G ` p ) -> A. x e. ( Base ` K ) ( F ` x ) = ( G ` x ) ) )
71243adant3 1081 . . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> F : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
72 f1ofn 6138 . . . . 5 |- ( F : ( Base ` K ) -1-1-onto-> ( Base ` K ) -> F Fn ( Base ` K ) )
7371, 72syl 17 . . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> F Fn ( Base ` K ) )
7463adant2 1080 . . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> G : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
75 f1ofn 6138 . . . . 5 |- ( G : ( Base ` K ) -1-1-onto-> ( Base ` K ) -> G Fn ( Base ` K ) )
7674, 75syl 17 . . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> G Fn ( Base ` K ) )
77 eqfnfv 6311 . . . 4 |- ( ( F Fn ( Base ` K ) /\ G Fn ( Base ` K ) ) -> ( F = G <-> A. x e. ( Base ` K ) ( F ` x ) = ( G ` x ) ) )
7873, 76, 77syl2anc 693 . . 3 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( F = G <-> A. x e. ( Base ` K ) ( F ` x ) = ( G ` x ) ) )
7970, 78sylibrd 249 . 2 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( A. p e. A ( F ` p ) = ( G ` p ) -> F = G ) )
80 fveq1 6190 . . 3 |- ( F = G -> ( F ` p ) = ( G ` p ) )
8180ralrimivw 2967 . 2 |- ( F = G -> A. p e. A ( F ` p ) = ( G ` p ) )
8279, 81impbid1 215 1 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( A. p e. A ( F ` p ) = ( G ` p ) <-> F = G ) )
Colors of variables: wff setvar class
Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   A.wral 2912   class class class wbr 4653   `'ccnv 5113   Fn wfn 5883   -1-1-onto->wf1o 5887   ` cfv 5888   Basecbs 15857   lecple 15948   Atomscatm 34550   HLchlt 34637   LHypclh 35270   LAutclaut 35271   LTrncltrn 35387
This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949
This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-ral 2917  df-rex 2918  df-reu 2919  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-map 7859  df-preset 16928  df-poset 16946  df-plt 16958  df-lub 16974  df-glb 16975  df-join 16976  df-meet 16977  df-p0 17039  df-lat 17046  df-clat 17108  df-oposet 34463  df-ol 34465  df-oml 34466  df-covers 34553  df-ats 34554  df-atl 34585  df-cvlat 34609  df-hlat 34638  df-lhyp 35274  df-laut 35275  df-ldil 35390  df-ltrn 35391
This theorem is referenced by:  ltrneq  35435  cdlemd  35494
  Copyright terms: Public domain W3C validator