smprngopr - Mathbox for Jeff Madsen

	Mathbox for Jeff Madsen		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > smprngopr		Structured version Visualization version Unicode version

Theorem smprngopr 33851

Description: A simple ring (one whose only ideals are

and

) is a prime ring. (Contributed by Jeff Madsen, 6-Jan-2011.)

**Hypotheses**
Ref	Expression
smprngpr.1
smprngpr.2
smprngpr.3
smprngpr.4	GId
smprngpr.5	GId

**Assertion**
Ref	Expression
smprngopr	$/\$ $/\$

Proof of Theorem smprngopr Dummy variables

are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		simp1 1061	. 2 $/\$ $/\$
2		smprngpr.1	. . . . 5
3		smprngpr.4	. . . . 5 GId
4	2, 3	0idl 33824	. . . 4
5	4	3ad2ant1 1082	. . 3 $/\$ $/\$
6		smprngpr.2	. . . . . . . 8
7		smprngpr.3	. . . . . . . 8
8		smprngpr.5	. . . . . . . 8 GId
9	2, 6, 7, 3, 8	0rngo 33826	. . . . . . 7
10		eqcom 2629	. . . . . . 7
11		eqcom 2629	. . . . . . 7
12	9, 10, 11	3bitr4g 303	. . . . . 6
13	12	necon3bid 2838	. . . . 5
14	13	biimpa 501	. . . 4 $/\$
15	14	3adant3 1081	. . 3 $/\$ $/\$
16		df-pr 4180	. . . . . . . 8
17	16	eqeq2i 2634	. . . . . . 7
18		eleq2 2690	. . . . . . . . 9
19		eleq2 2690	. . . . . . . . 9
20	18, 19	anbi12d 747	. . . . . . . 8 $/\$ $/\$
21		elun 3753	. . . . . . . . . 10 $\/$
22		velsn 4193	. . . . . . . . . . 11
23		velsn 4193	. . . . . . . . . . 11
24	22, 23	orbi12i 543	. . . . . . . . . 10 $\/$ $\/$
25	21, 24	bitri 264	. . . . . . . . 9 $\/$
26		elun 3753	. . . . . . . . . 10 $\/$
27		velsn 4193	. . . . . . . . . . 11
28		velsn 4193	. . . . . . . . . . 11
29	27, 28	orbi12i 543	. . . . . . . . . 10 $\/$ $\/$
30	26, 29	bitri 264	. . . . . . . . 9 $\/$
31	25, 30	anbi12i 733	. . . . . . . 8 $/\$ $\/$ $/\$ $\/$
32	20, 31	syl6bb 276	. . . . . . 7 $/\$ $\/$ $/\$ $\/$
33	17, 32	sylbi 207	. . . . . 6 $/\$ $\/$ $/\$ $\/$
34	33	3ad2ant3 1084	. . . . 5 $/\$ $/\$ $/\$ $\/$ $/\$ $\/$
35		eqimss 3657	. . . . . . . . . . 11
36	35	orcd 407	. . . . . . . . . 10 $\/$
37	36	adantr 481	. . . . . . . . 9 $/\$ $\/$
38	37	a1d 25	. . . . . . . 8 $/\$ $\/$
39	38	a1i 11	. . . . . . 7 $/\$ $/\$ $\/$
40		eqimss 3657	. . . . . . . . . . 11
41	40	olcd 408	. . . . . . . . . 10 $\/$
42	41	adantl 482	. . . . . . . . 9 $/\$ $\/$
43	42	a1d 25	. . . . . . . 8 $/\$ $\/$
44	43	a1i 11	. . . . . . 7 $/\$ $/\$ $\/$
45	36	adantr 481	. . . . . . . . 9 $/\$ $\/$
46	45	a1d 25	. . . . . . . 8 $/\$ $\/$
47	46	a1i 11	. . . . . . 7 $/\$ $/\$ $\/$
48	2	rneqi 5352	. . . . . . . . . . . . . 14
49	7, 48	eqtri 2644	. . . . . . . . . . . . 13
50	49, 6, 8	rngo1cl 33738	. . . . . . . . . . . 12
51	50	adantr 481	. . . . . . . . . . 11 $/\$
52	6, 49, 8	rngolidm 33736	. . . . . . . . . . . . . . . 16 $/\$
53	50, 52	mpdan 702	. . . . . . . . . . . . . . 15
54	53	eleq1d 2686	. . . . . . . . . . . . . 14
55		fvex 6201	. . . . . . . . . . . . . . . 16 GId
56	8, 55	eqeltri 2697	. . . . . . . . . . . . . . 15
57	56	elsn 4192	. . . . . . . . . . . . . 14
58	54, 57	syl6bb 276	. . . . . . . . . . . . 13
59	58	necon3bbid 2831	. . . . . . . . . . . 12
60	59	biimpar 502	. . . . . . . . . . 11 $/\$
61		oveq1 6657	. . . . . . . . . . . . . 14
62	61	eleq1d 2686	. . . . . . . . . . . . 13
63	62	notbid 308	. . . . . . . . . . . 12
64		oveq2 6658	. . . . . . . . . . . . . 14
65	64	eleq1d 2686	. . . . . . . . . . . . 13
66	65	notbid 308	. . . . . . . . . . . 12
67	63, 66	rspc2ev 3324	. . . . . . . . . . 11 $/\$ $/\$
68	51, 51, 60, 67	syl3anc 1326	. . . . . . . . . 10 $/\$
69		rexnal2 3043	. . . . . . . . . 10
70	68, 69	sylib 208	. . . . . . . . 9 $/\$
71	70	pm2.21d 118	. . . . . . . 8 $/\$ $\/$
72		raleq 3138	. . . . . . . . . 10
73		raleq 3138	. . . . . . . . . . 11
74	73	ralbidv 2986	. . . . . . . . . 10
75	72, 74	sylan9bb 736	. . . . . . . . 9 $/\$
76	75	imbi1d 331	. . . . . . . 8 $/\$ $\/$ $\/$
77	71, 76	syl5ibrcom 237	. . . . . . 7 $/\$ $/\$ $\/$
78	39, 44, 47, 77	ccased 988	. . . . . 6 $/\$ $\/$ $/\$ $\/$ $\/$
79	78	3adant3 1081	. . . . 5 $/\$ $/\$ $\/$ $/\$ $\/$ $\/$
80	34, 79	sylbid 230	. . . 4 $/\$ $/\$ $/\$ $\/$
81	80	ralrimivv 2970	. . 3 $/\$ $/\$ $\/$
82	2, 6, 7	ispridl 33833	. . . 4 $/\$ $/\$ $\/$
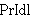
83	82	3ad2ant1 1082	. . 3 $/\$ $/\$ $/\$ $/\$ $\/$
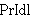
84	5, 15, 81, 83	mpbir3and 1245	. 2 $/\$ $/\$
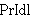85	2, 3	isprrngo 33849	. 2 $/\$
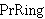86	1, 84, 85	sylanbrc 698	1 $/\$ $/\$

Colors of variables: wff setvar class

Syntax hints:

wn 3

wi 4

wb 196 $\/$ wo 383 $/\$ wa 384 $/\$ w3a 1037

wceq 1483

wcel 1990

wne 2794

wral 2912

wrex 2913

cvv 3200

cun 3572

wss 3574

csn 4177

cpr 4179

crn 5115

cfv 5888 (class class class)co 6650

c1st 7166

c2nd 7167 GIdcgi 27344

crngo 33693

cidl 33806

cpridl 33807

cprrng 33845

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-ral 2917 df-rex 2918 df-reu 2919 df-rmo 2920 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-1st 7168 df-2nd 7169 df-grpo 27347 df-gid 27348 df-ginv 27349 df-ablo 27399 df-ass 33642 df-exid 33644 df-mgmOLD 33648 df-sgrOLD 33660 df-mndo 33666 df-rngo 33694 df-idl 33809 df-pridl 33810 df-prrngo 33847

This theorem is referenced by: divrngpr 33852

W3C validator