4atexlemcnd - Mathbox for Norm Megill

	Mathbox for Norm Megill		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > 4atexlemcnd		Structured version Visualization version Unicode version

Theorem 4atexlemcnd 35358

Description: Lemma for 4atexlem7 35361. (Contributed by NM, 24-Nov-2012.)

**Hypotheses**
Ref	Expression
4thatlem.ph	$/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$
4thatlem0.l
4thatlem0.j	$.\/$
4thatlem0.m	$./\$
4thatlem0.a
4thatlem0.h
4thatlem0.u	$.\/$ $./\$
4thatlem0.v	$.\/$ $./\$
4thatlem0.c	$.\/$ $./\$ $.\/$
4thatlem0.d	$.\/$ $./\$ $.\/$

**Assertion**
Ref	Expression
4atexlemcnd

**Proof of Theorem 4atexlemcnd**
Step	Hyp	Ref	Expression
1		4thatlem.ph	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$
2		4thatlem0.l	. . . 4
3		4thatlem0.j	. . . 4 $.\/$
4		4thatlem0.m	. . . 4 $./\$
5		4thatlem0.a	. . . 4
6		4thatlem0.h	. . . 4
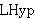7		4thatlem0.u	. . . 4 $.\/$ $./\$
8		4thatlem0.v	. . . 4 $.\/$ $./\$
9	1, 2, 3, 4, 5, 6, 7, 8	4atexlemtlw 35353	. . 3
10		4thatlem0.c	. . . 4 $.\/$ $./\$ $.\/$
11	1, 2, 3, 4, 5, 6, 7, 8, 10	4atexlemnclw 35356	. . 3
12		nbrne2 4673	. . 3 $/\$
13	9, 11, 12	syl2anc 693	. 2
14	1	4atexlemk 35333	. . . . . . . . 9
15	1	4atexlemq 35337	. . . . . . . . 9
16	1	4atexlemt 35339	. . . . . . . . 9
17	3, 5	hlatjcom 34654	. . . . . . . . 9 $/\$ $/\$ $.\/$ $.\/$
18	14, 15, 16, 17	syl3anc 1326	. . . . . . . 8 $.\/$ $.\/$
19		simp221 1202	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$
20	1, 19	sylbi 207	. . . . . . . . 9
21	3, 5	hlatjcom 34654	. . . . . . . . 9 $/\$ $/\$ $.\/$ $.\/$
22	14, 20, 16, 21	syl3anc 1326	. . . . . . . 8 $.\/$ $.\/$
23	18, 22	oveq12d 6668	. . . . . . 7 $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$
24	1	4atexlemkc 35344	. . . . . . . . 9
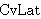25	1	4atexlemp 35336	. . . . . . . . 9
26	1	4atexlempnq 35341	. . . . . . . . 9
27		simp223 1204	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $.\/$ $.\/$
28	1, 27	sylbi 207	. . . . . . . . 9 $.\/$ $.\/$
29	5, 3	cvlsupr6 34634	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
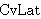
30	29	necomd 2849	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
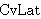
31	24, 25, 15, 20, 26, 28, 30	syl132anc 1344	. . . . . . . 8
32	1, 2, 3, 4, 5, 6, 7, 8	4atexlemntlpq 35354	. . . . . . . . 9 $.\/$
33	5, 3	cvlsupr7 34635	. . . . . . . . . . . 12 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
34	24, 25, 15, 20, 26, 28, 33	syl132anc 1344	. . . . . . . . . . 11 $.\/$ $.\/$
35	3, 5	hlatjcom 34654	. . . . . . . . . . . 12 $/\$ $/\$ $.\/$ $.\/$
36	14, 15, 20, 35	syl3anc 1326	. . . . . . . . . . 11 $.\/$ $.\/$
37	34, 36	eqtr4d 2659	. . . . . . . . . 10 $.\/$ $.\/$
38	37	breq2d 4665	. . . . . . . . 9 $.\/$ $.\/$
39	32, 38	mtbid 314	. . . . . . . 8 $.\/$
40	2, 3, 4, 5	2llnma2 35075	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
41	14, 15, 20, 16, 31, 39, 40	syl132anc 1344	. . . . . . 7 $.\/$ $./\$ $.\/$
42	23, 41	eqtr2d 2657	. . . . . 6 $.\/$ $./\$ $.\/$
43	42	adantr 481	. . . . 5 $/\$ $.\/$ $./\$ $.\/$
44	1	4atexlemkl 35343	. . . . . . . . . 10
45	1, 3, 5	4atexlemqtb 35347	. . . . . . . . . 10 $.\/$
46	1, 3, 5	4atexlempsb 35346	. . . . . . . . . 10 $.\/$
47		eqid 2622	. . . . . . . . . . 11
48	47, 2, 4	latmle1 17076	. . . . . . . . . 10 $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$
49	44, 45, 46, 48	syl3anc 1326	. . . . . . . . 9 $.\/$ $./\$ $.\/$ $.\/$
50	10, 49	syl5eqbr 4688	. . . . . . . 8 $.\/$
51	50	adantr 481	. . . . . . 7 $/\$ $.\/$
52		simpr 477	. . . . . . . 8 $/\$
53		4thatlem0.d	. . . . . . . . . 10 $.\/$ $./\$ $.\/$
54	47, 3, 5	hlatjcl 34653	. . . . . . . . . . . 12 $/\$ $/\$ $.\/$
55	14, 20, 16, 54	syl3anc 1326	. . . . . . . . . . 11 $.\/$
56	47, 2, 4	latmle1 17076	. . . . . . . . . . 11 $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$
57	44, 55, 46, 56	syl3anc 1326	. . . . . . . . . 10 $.\/$ $./\$ $.\/$ $.\/$
58	53, 57	syl5eqbr 4688	. . . . . . . . 9 $.\/$
59	58	adantr 481	. . . . . . . 8 $/\$ $.\/$
60	52, 59	eqbrtrd 4675	. . . . . . 7 $/\$ $.\/$
61	1, 2, 3, 4, 5, 6, 7, 8, 10	4atexlemc 35355	. . . . . . . . . 10
62	47, 5	atbase 34576	. . . . . . . . . 10
63	61, 62	syl 17	. . . . . . . . 9
64	47, 2, 4	latlem12 17078	. . . . . . . . 9 $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
65	44, 63, 45, 55, 64	syl13anc 1328	. . . . . . . 8 $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
66	65	adantr 481	. . . . . . 7 $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
67	51, 60, 66	mpbi2and 956	. . . . . 6 $/\$ $.\/$ $./\$ $.\/$
68		hlatl 34647	. . . . . . . . 9
69	14, 68	syl 17	. . . . . . . 8
70	42, 16	eqeltrrd 2702	. . . . . . . 8 $.\/$ $./\$ $.\/$
71	2, 5	atcmp 34598	. . . . . . . 8 $/\$ $/\$ $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$
72	69, 61, 70, 71	syl3anc 1326	. . . . . . 7 $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$
73	72	adantr 481	. . . . . 6 $/\$ $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$
74	67, 73	mpbid 222	. . . . 5 $/\$ $.\/$ $./\$ $.\/$
75	43, 74	eqtr4d 2659	. . . 4 $/\$
76	75	ex 450	. . 3
77	76	necon3d 2815	. 2
78	13, 77	mpd 15	1

Colors of variables: wff setvar class

Syntax hints:

wn 3

wi 4

wb 196 $/\$ wa 384 $/\$ w3a 1037

wceq 1483

wcel 1990

wne 2794 class class class wbr 4653

cfv 5888 (class class class)co 6650

cbs 15857

cple 15948

cjn 16944

cmee 16945

clat 17045

catm 34550

cal 34551

clc 34552

chlt 34637

clh 35270

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-ral 2917 df-rex 2918 df-reu 2919 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-preset 16928 df-poset 16946 df-plt 16958 df-lub 16974 df-glb 16975 df-join 16976 df-meet 16977 df-p0 17039 df-p1 17040 df-lat 17046 df-clat 17108 df-oposet 34463 df-ol 34465 df-oml 34466 df-covers 34553 df-ats 34554 df-atl 34585 df-cvlat 34609 df-hlat 34638 df-llines 34784 df-lplanes 34785 df-lhyp 35274

This theorem is referenced by: 4atexlemex4 35359

W3C validator