4atexlemnclw - Mathbox for Norm Megill

	Mathbox for Norm Megill		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > 4atexlemnclw		Structured version Visualization version Unicode version

Theorem 4atexlemnclw 35356

Description: Lemma for 4atexlem7 35361. (Contributed by NM, 24-Nov-2012.)

**Hypotheses**
Ref	Expression
4thatlem.ph	$/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$
4thatlem0.l
4thatlem0.j	$.\/$
4thatlem0.m	$./\$
4thatlem0.a
4thatlem0.h
4thatlem0.u	$.\/$ $./\$
4thatlem0.v	$.\/$ $./\$
4thatlem0.c	$.\/$ $./\$ $.\/$

**Assertion**
Ref	Expression
4atexlemnclw

**Proof of Theorem 4atexlemnclw**
Step	Hyp	Ref	Expression
1		4thatlem0.c	. . . 4 $.\/$ $./\$ $.\/$
2		4thatlem.ph	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$
3	2	4atexlemkl 35343	. . . . 5
4		4thatlem0.j	. . . . . 6 $.\/$
5		4thatlem0.a	. . . . . 6
6	2, 4, 5	4atexlemqtb 35347	. . . . 5 $.\/$
7	2, 4, 5	4atexlempsb 35346	. . . . 5 $.\/$
8		eqid 2622	. . . . . 6
9		4thatlem0.l	. . . . . 6
10		4thatlem0.m	. . . . . 6 $./\$
11	8, 9, 10	latmle1 17076	. . . . 5 $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$
12	3, 6, 7, 11	syl3anc 1326	. . . 4 $.\/$ $./\$ $.\/$ $.\/$
13	1, 12	syl5eqbr 4688	. . 3 $.\/$
14		simp13r 1177	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$
15	2, 14	sylbi 207	. . . 4
16	2	4atexlemkc 35344	. . . . . 6
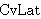17		4thatlem0.h	. . . . . . 7
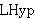18		4thatlem0.u	. . . . . . 7 $.\/$ $./\$
19		4thatlem0.v	. . . . . . 7 $.\/$ $./\$
20	2, 9, 4, 10, 5, 17, 18, 19	4atexlemv 35351	. . . . . 6
21	2	4atexlemq 35337	. . . . . 6
22	2	4atexlemt 35339	. . . . . 6
23	2, 9, 4, 10, 5, 17, 18	4atexlemu 35350	. . . . . . 7
24	2, 9, 4, 10, 5, 17, 18, 19	4atexlemunv 35352	. . . . . . 7
25	2	4atexlemutvt 35340	. . . . . . 7 $.\/$ $.\/$
26	5, 4	cvlsupr6 34634	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
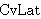
27	26	necomd 2849	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
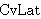
28	16, 23, 20, 22, 24, 25, 27	syl132anc 1344	. . . . . 6
29	9, 4, 5	cvlatexch2 34624	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
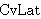
30	16, 20, 21, 22, 28, 29	syl131anc 1339	. . . . 5 $.\/$ $.\/$
31	2, 17	4atexlemwb 35345	. . . . . . . . 9
32	8, 9, 10	latmle2 17077	. . . . . . . . 9 $/\$ $.\/$ $/\$ $.\/$ $./\$
33	3, 7, 31, 32	syl3anc 1326	. . . . . . . 8 $.\/$ $./\$
34	19, 33	syl5eqbr 4688	. . . . . . 7
35	2, 9, 4, 10, 5, 17, 18, 19	4atexlemtlw 35353	. . . . . . 7
36	8, 5	atbase 34576	. . . . . . . . 9
37	20, 36	syl 17	. . . . . . . 8
38	8, 5	atbase 34576	. . . . . . . . 9
39	22, 38	syl 17	. . . . . . . 8
40	8, 9, 4	latjle12 17062	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $.\/$
41	3, 37, 39, 31, 40	syl13anc 1328	. . . . . . 7 $/\$ $.\/$
42	34, 35, 41	mpbi2and 956	. . . . . 6 $.\/$
43	8, 5	atbase 34576	. . . . . . . 8
44	21, 43	syl 17	. . . . . . 7
45	2	4atexlemk 35333	. . . . . . . 8
46	8, 4, 5	hlatjcl 34653	. . . . . . . 8 $/\$ $/\$ $.\/$
47	45, 20, 22, 46	syl3anc 1326	. . . . . . 7 $.\/$
48	8, 9	lattr 17056	. . . . . . 7 $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$
49	3, 44, 47, 31, 48	syl13anc 1328	. . . . . 6 $.\/$ $/\$ $.\/$
50	42, 49	mpan2d 710	. . . . 5 $.\/$
51	30, 50	syld 47	. . . 4 $.\/$
52	15, 51	mtod 189	. . 3 $.\/$
53		nbrne2 4673	. . 3 $.\/$ $/\$ $.\/$
54	13, 52, 53	syl2anc 693	. 2
55	2	4atexlemw 35334	. . . 4
56	45, 55	jca 554	. . 3 $/\$
57	2	4atexlempw 35335	. . 3 $/\$
58	2	4atexlems 35338	. . 3
59	2, 9, 4, 10, 5, 17, 18, 19, 1	4atexlemc 35355	. . 3
60	2, 9, 4, 5	4atexlempns 35348	. . 3
61	8, 9, 10	latmle2 17077	. . . . 5 $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$
62	3, 6, 7, 61	syl3anc 1326	. . . 4 $.\/$ $./\$ $.\/$ $.\/$
63	1, 62	syl5eqbr 4688	. . 3 $.\/$
64	9, 4, 10, 5, 17, 19	lhpat3 35332	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$
65	56, 57, 58, 59, 60, 63, 64	syl222anc 1342	. 2
66	54, 65	mpbird 247	1

Colors of variables: wff setvar class

Syntax hints:

wn 3

wi 4

wb 196 $/\$ wa 384 $/\$ w3a 1037

wceq 1483

wcel 1990

wne 2794 class class class wbr 4653

cfv 5888 (class class class)co 6650

cbs 15857

cple 15948

cjn 16944

cmee 16945

clat 17045

catm 34550

clc 34552

chlt 34637

clh 35270

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-ral 2917 df-rex 2918 df-reu 2919 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-preset 16928 df-poset 16946 df-plt 16958 df-lub 16974 df-glb 16975 df-join 16976 df-meet 16977 df-p0 17039 df-p1 17040 df-lat 17046 df-clat 17108 df-oposet 34463 df-ol 34465 df-oml 34466 df-covers 34553 df-ats 34554 df-atl 34585 df-cvlat 34609 df-hlat 34638 df-llines 34784 df-lplanes 34785 df-lhyp 35274

This theorem is referenced by: 4atexlemex2 35357 4atexlemcnd 35358

W3C validator