cdlemg6c - Mathbox for Norm Megill

	Mathbox for Norm Megill		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > cdlemg6c		Structured version Visualization version Unicode version

Theorem cdlemg6c 35908

Description: TODO: FIX COMMENT. (Contributed by NM, 27-Apr-2013.)

**Hypotheses**
Ref	Expression
cdlemg4.l
cdlemg4.a
cdlemg4.h
cdlemg4.t
cdlemg4.r
cdlemg4.j	$.\/$
cdlemg4b.v

**Assertion**
Ref	Expression
cdlemg6c	$/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $.\/$

Distinct variable groups:

$.\/$ ,

Allowed substitution hint:

(

)

**Proof of Theorem cdlemg6c**
Step	Hyp	Ref	Expression
1		simpl1 1064	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
2		simprl 794	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
3		simpl22 1140	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
4		simpl23 1141	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
5		simpl31 1142	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
6		simprr 796	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
7		simpl1l 1112	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
8		simp22l 1180	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
9	8	adantr 481	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
10		simprll 802	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
11		cdlemg4b.v	. . . . . . 7
12		eqid 2622	. . . . . . . . 9
13		cdlemg4.h	. . . . . . . . 9
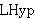14		cdlemg4.t	. . . . . . . . 9
15		cdlemg4.r	. . . . . . . . 9
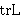16	12, 13, 14, 15	trlcl 35451	. . . . . . . 8 $/\$ $/\$
17	1, 5, 16	syl2anc 693	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
18	11, 17	syl5eqel 2705	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
19		simp22r 1181	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
20	19	adantr 481	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
21		cdlemg4.l	. . . . . . . . . . 11
22	21, 13, 14, 15	trlle 35471	. . . . . . . . . 10 $/\$ $/\$
23	1, 5, 22	syl2anc 693	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
24	11, 23	syl5eqbr 4688	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
25		simp1l 1085	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
26		hllat 34650	. . . . . . . . . . 11
27	25, 26	syl 17	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
28	27	adantr 481	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
29		cdlemg4.a	. . . . . . . . . . . 12
30	12, 29	atbase 34576	. . . . . . . . . . 11
31	8, 30	syl 17	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
32	31	adantr 481	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
33		simp1r 1086	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
34	12, 13	lhpbase 35284	. . . . . . . . . . 11
35	33, 34	syl 17	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
36	35	adantr 481	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
37	12, 21	lattr 17056	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$
38	28, 32, 18, 36, 37	syl13anc 1328	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
39	24, 38	mpan2d 710	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
40	20, 39	mtod 189	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
41		cdlemg4.j	. . . . . . 7 $.\/$
42	12, 21, 41, 29	hlexch2 34669	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
43	7, 9, 10, 18, 40, 42	syl131anc 1339	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$
44		simpl32 1143	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
45		simp21l 1178	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
46	45	adantr 481	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
47	12, 29	atbase 34576	. . . . . . . . 9
48	46, 47	syl 17	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
49	12, 21, 41	latlej2 17061	. . . . . . . 8 $/\$ $/\$ $.\/$
50	28, 48, 18, 49	syl3anc 1326	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
51	12, 41	latjcl 17051	. . . . . . . . 9 $/\$ $/\$ $.\/$
52	28, 48, 18, 51	syl3anc 1326	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
53	12, 21, 41	latjle12 17062	. . . . . . . 8 $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
54	28, 32, 18, 52, 53	syl13anc 1328	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
55	44, 50, 54	mpbi2and 956	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$
56	12, 29	atbase 34576	. . . . . . . 8
57	10, 56	syl 17	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
58	12, 41	latjcl 17051	. . . . . . . 8 $/\$ $/\$ $.\/$
59	28, 32, 18, 58	syl3anc 1326	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
60	12, 21	lattr 17056	. . . . . . 7 $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
61	28, 57, 59, 52, 60	syl13anc 1328	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
62	55, 61	mpan2d 710	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$
63	43, 62	syld 47	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$
64	6, 63	mtod 189	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$
65		simpl21 1139	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
66		simpl33 1144	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
67	21, 29, 13, 14, 15, 41, 11	cdlemg6a 35906	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
68	1, 65, 2, 4, 5, 6, 66, 67	syl133anc 1349	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
69	21, 29, 13, 14, 15, 41, 11	cdlemg6b 35907	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$
70	1, 2, 3, 4, 5, 64, 68, 69	syl133anc 1349	. 2 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $.\/$
71	70	ex 450	1 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $/\$ $/\$ $.\/$

Colors of variables: wff setvar class

Syntax hints:

wn 3

wi 4

wb 196 $/\$ wa 384 $/\$ w3a 1037

wceq 1483

wcel 1990 class class class wbr 4653

cfv 5888 (class class class)co 6650

cbs 15857

cple 15948

cjn 16944

clat 17045

catm 34550

chlt 34637

clh 35270

cltrn 35387

ctrl 35445

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949 ax-riotaBAD 34239

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3or 1038 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-nel 2898 df-ral 2917 df-rex 2918 df-reu 2919 df-rmo 2920 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-iin 4523 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-mpt2 6655 df-1st 7168 df-2nd 7169 df-undef 7399 df-map 7859 df-preset 16928 df-poset 16946 df-plt 16958 df-lub 16974 df-glb 16975 df-join 16976 df-meet 16977 df-p0 17039 df-p1 17040 df-lat 17046 df-clat 17108 df-oposet 34463 df-ol 34465 df-oml 34466 df-covers 34553 df-ats 34554 df-atl 34585 df-cvlat 34609 df-hlat 34638 df-llines 34784 df-lplanes 34785 df-lvols 34786 df-lines 34787 df-psubsp 34789 df-pmap 34790 df-padd 35082 df-lhyp 35274 df-laut 35275 df-ldil 35390 df-ltrn 35391 df-trl 35446

This theorem is referenced by: cdlemg6d 35909

W3C validator