dalem54 - Mathbox for Norm Megill

	Mathbox for Norm Megill		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > dalem54		Structured version Visualization version Unicode version

Theorem dalem54 35012

Description: Lemma for dath 35022. Line

intersects the auxiliary axis of perspectivity

. (Contributed by NM, 8-Aug-2012.)

**Hypotheses**
Ref	Expression
dalem.ph	$/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$
dalem.l
dalem.j	$.\/$
dalem.a
dalem.ps	$/\$ $/\$ $/\$ $/\$ $/\$ $.\/$
dalem54.m	$./\$
dalem54.o
dalem54.y	$.\/$ $.\/$
dalem54.z	$.\/$ $.\/$
dalem54.g	$.\/$ $./\$ $.\/$
dalem54.h	$.\/$ $./\$ $.\/$
dalem54.i	$.\/$ $./\$ $.\/$
dalem54.b1	$.\/$ $.\/$ $./\$

**Assertion**
Ref	Expression
dalem54	$/\$ $/\$ $.\/$ $./\$

**Proof of Theorem dalem54**
Step	Hyp	Ref	Expression
1		dalem.ph	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$
2	1	dalemkehl 34909	. . 3
3	2	3ad2ant1 1082	. 2 $/\$ $/\$
4		dalem.l	. . . 4
5		dalem.j	. . . 4 $.\/$
6		dalem.a	. . . 4
7		dalem.ps	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$
8		dalem54.m	. . . 4 $./\$
9		dalem54.o	. . . 4
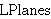10		dalem54.y	. . . 4 $.\/$ $.\/$
11		dalem54.z	. . . 4 $.\/$ $.\/$
12		dalem54.g	. . . 4 $.\/$ $./\$ $.\/$
13	1, 4, 5, 6, 7, 8, 9, 10, 11, 12	dalem23 34982	. . 3 $/\$ $/\$
14		dalem54.h	. . . 4 $.\/$ $./\$ $.\/$
15	1, 4, 5, 6, 7, 8, 9, 10, 11, 14	dalem29 34987	. . 3 $/\$ $/\$
16		dalem54.i	. . . 4 $.\/$ $./\$ $.\/$
17	1, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 16	dalem41 34999	. . 3 $/\$ $/\$
18		eqid 2622	. . . 4
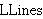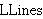19	5, 6, 18	llni2 34798	. . 3 $/\$ $/\$ $/\$ $.\/$
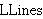20	3, 13, 15, 17, 19	syl31anc 1329	. 2 $/\$ $/\$ $.\/$
21		dalem54.b1	. . 3 $.\/$ $.\/$ $./\$
22	1, 4, 5, 6, 7, 8, 18, 9, 10, 11, 12, 14, 16, 21	dalem53 35011	. 2 $/\$ $/\$
23	1	dalemkelat 34910	. . . . . . 7
24	23	3ad2ant1 1082	. . . . . 6 $/\$ $/\$
25		eqid 2622	. . . . . . . . 9
26	25, 18	llnbase 34795	. . . . . . . 8 $.\/$ $.\/$
27	20, 26	syl 17	. . . . . . 7 $/\$ $/\$ $.\/$
28	1, 4, 5, 6, 7, 8, 9, 10, 11, 16	dalem34 34992	. . . . . . . 8 $/\$ $/\$
29	25, 6	atbase 34576	. . . . . . . 8
30	28, 29	syl 17	. . . . . . 7 $/\$ $/\$
31	25, 5	latjcl 17051	. . . . . . 7 $/\$ $.\/$ $/\$ $.\/$ $.\/$
32	24, 27, 30, 31	syl3anc 1326	. . . . . 6 $/\$ $/\$ $.\/$ $.\/$
33	1, 9	dalemyeb 34935	. . . . . . 7
34	33	3ad2ant1 1082	. . . . . 6 $/\$ $/\$
35	25, 4, 8	latmle2 17077	. . . . . 6 $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $./\$
36	24, 32, 34, 35	syl3anc 1326	. . . . 5 $/\$ $/\$ $.\/$ $.\/$ $./\$
37	21, 36	syl5eqbr 4688	. . . 4 $/\$ $/\$
38	1, 4, 5, 6, 7, 8, 9, 10, 11, 12	dalem24 34983	. . . . 5 $/\$ $/\$
39	25, 6	atbase 34576	. . . . . . . 8
40	13, 39	syl 17	. . . . . . 7 $/\$ $/\$
41	25, 6	atbase 34576	. . . . . . . 8
42	15, 41	syl 17	. . . . . . 7 $/\$ $/\$
43	25, 4, 5	latjle12 17062	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $.\/$
44	24, 40, 42, 34, 43	syl13anc 1328	. . . . . 6 $/\$ $/\$ $/\$ $.\/$
45		simpl 473	. . . . . 6 $/\$
46	44, 45	syl6bir 244	. . . . 5 $/\$ $/\$ $.\/$
47	38, 46	mtod 189	. . . 4 $/\$ $/\$ $.\/$
48		nbrne2 4673	. . . 4 $/\$ $.\/$ $.\/$
49	37, 47, 48	syl2anc 693	. . 3 $/\$ $/\$ $.\/$
50	49	necomd 2849	. 2 $/\$ $/\$ $.\/$
51		hlatl 34647	. . . 4
52	3, 51	syl 17	. . 3 $/\$ $/\$
53	25, 18	llnbase 34795	. . . . 5
54	22, 53	syl 17	. . . 4 $/\$ $/\$
55	25, 8	latmcl 17052	. . . 4 $/\$ $.\/$ $/\$ $.\/$ $./\$
56	24, 27, 54, 55	syl3anc 1326	. . 3 $/\$ $/\$ $.\/$ $./\$
57	1, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 16	dalem52 35010	. . 3 $/\$ $/\$ $.\/$ $./\$ $.\/$
58	1, 5, 6	dalempjqeb 34931	. . . . . 6 $.\/$
59	58	3ad2ant1 1082	. . . . 5 $/\$ $/\$ $.\/$
60	25, 4, 8	latmle1 17076	. . . . 5 $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$
61	24, 27, 59, 60	syl3anc 1326	. . . 4 $/\$ $/\$ $.\/$ $./\$ $.\/$ $.\/$
62	1, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 16	dalem51 35009	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
63	62	simpld 475	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$
64	25, 6	atbase 34576	. . . . . . . 8
65	64	anim2i 593	. . . . . . 7 $/\$ $/\$
66	65	3anim1i 1248	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
67		biid 251	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$
68		eqid 2622	. . . . . . 7 $.\/$ $.\/$ $.\/$ $.\/$
69		eqid 2622	. . . . . . 7 $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$
70	67, 4, 5, 6, 8, 9, 68, 10, 21, 69	dalem10 34959	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
71	66, 70	syl3an1 1359	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
72	63, 71	syl 17	. . . 4 $/\$ $/\$ $.\/$ $./\$ $.\/$
73	25, 8	latmcl 17052	. . . . . 6 $/\$ $.\/$ $/\$ $.\/$ $.\/$ $./\$ $.\/$
74	24, 27, 59, 73	syl3anc 1326	. . . . 5 $/\$ $/\$ $.\/$ $./\$ $.\/$
75	25, 4, 8	latlem12 17078	. . . . 5 $/\$ $.\/$ $./\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $./\$ $.\/$ $.\/$ $/\$ $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$ $./\$
76	24, 74, 27, 54, 75	syl13anc 1328	. . . 4 $/\$ $/\$ $.\/$ $./\$ $.\/$ $.\/$ $/\$ $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$ $.\/$ $./\$
77	61, 72, 76	mpbi2and 956	. . 3 $/\$ $/\$ $.\/$ $./\$ $.\/$ $.\/$ $./\$
78		eqid 2622	. . . 4
79	25, 4, 78, 6	atlen0 34597	. . 3 $/\$ $.\/$ $./\$ $/\$ $.\/$ $./\$ $.\/$ $/\$ $.\/$ $./\$ $.\/$ $.\/$ $./\$ $.\/$ $./\$
80	52, 56, 57, 77, 79	syl31anc 1329	. 2 $/\$ $/\$ $.\/$ $./\$
81	8, 78, 6, 18	2llnmat 34810	. 2 $/\$ $.\/$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $./\$ $.\/$ $./\$
82	3, 20, 22, 50, 80, 81	syl32anc 1334	1 $/\$ $/\$ $.\/$ $./\$

Colors of variables: wff setvar class

Syntax hints:

wn 3

wi 4

wb 196 $/\$ wa 384 $/\$ w3a 1037

wceq 1483

wcel 1990

wne 2794 class class class wbr 4653

cfv 5888 (class class class)co 6650

cbs 15857

cple 15948

cjn 16944

cmee 16945

cp0 17037

clat 17045

catm 34550

cal 34551

chlt 34637

clln 34777

clpl 34778

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3or 1038 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-ral 2917 df-rex 2918 df-reu 2919 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-preset 16928 df-poset 16946 df-plt 16958 df-lub 16974 df-glb 16975 df-join 16976 df-meet 16977 df-p0 17039 df-lat 17046 df-clat 17108 df-oposet 34463 df-ol 34465 df-oml 34466 df-covers 34553 df-ats 34554 df-atl 34585 df-cvlat 34609 df-hlat 34638 df-llines 34784 df-lplanes 34785 df-lvols 34786

This theorem is referenced by: dalem55 35013 dalem57 35015

W3C validator