Theorem doca2N 36415

Description: Double orthocomplement of partial isomorphism A. (Contributed by NM, 6-Dec-2013.) (New usage is discouraged.)

Hypotheses

Ref	Expression
doca2.h	|- H = ( LHyp ` K )
doca2.i	|- I = ( ( DIsoA ` K ) ` W )
doca2.n	|- ._|_ = ( ( ocA ` K ) ` W )

Assertion

Ref	Expression
doca2N	|- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ._|_ ` ( ._|_ ` ( I ` X ) ) ) = ( I ` X ) )

Proof of Theorem doca2N

Step	Hyp	Ref	Expression
1		hlol 34648	. . . . . . . . . . . . 13 |- ( K e. HL -> K e. OL )
2	1	ad2antrr 762	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> K e. OL )
3		eqid 2622	. . . . . . . . . . . . 13 |- ( Base ` K ) = ( Base ` K )
4		doca2.h	. . . . . . . . . . . . 13 |- H = ( LHyp ` K )
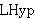5		doca2.i	. . . . . . . . . . . . 13 |- I = ( ( DIsoA ` K ) ` W )
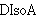6	3, 4, 5	diadmclN 36326	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> X e. ( Base ` K ) )
7	3, 4	lhpbase 35284	. . . . . . . . . . . . 13 |- ( W e. H -> W e. ( Base ` K ) )
8	7	ad2antlr 763	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> W e. ( Base ` K ) )
9		eqid 2622	. . . . . . . . . . . . 13 |- ( join ` K ) = ( join ` K )
10		eqid 2622	. . . . . . . . . . . . 13 |- ( meet ` K ) = ( meet ` K )
11		eqid 2622	. . . . . . . . . . . . 13 |- ( oc ` K ) = ( oc ` K )
12	3, 9, 10, 11	oldmm1 34504	. . . . . . . . . . . 12 |- ( ( K e. OL /\ X e. ( Base ` K ) /\ W e. ( Base ` K ) ) -> ( ( oc ` K ) ` ( X ( meet ` K ) W ) ) = ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
13	2, 6, 8, 12	syl3anc 1326	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( oc ` K ) ` ( X ( meet ` K ) W ) ) = ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
14	13	oveq1d 6665	. . . . . . . . . 10 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( oc ` K ) ` ( X ( meet ` K ) W ) ) ( meet ` K ) W ) = ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) )
15	14	eqcomd 2628	. . . . . . . . 9 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) = ( ( ( oc ` K ) ` ( X ( meet ` K ) W ) ) ( meet ` K ) W ) )
16	15	fveq2d 6195	. . . . . . . 8 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) = ( ( oc ` K ) ` ( ( ( oc ` K ) ` ( X ( meet ` K ) W ) ) ( meet ` K ) W ) ) )
17		hllat 34650	. . . . . . . . . . 11 |- ( K e. HL -> K e. Lat )
18	17	ad2antrr 762	. . . . . . . . . 10 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> K e. Lat )
19	3, 10	latmcl 17052	. . . . . . . . . 10 |- ( ( K e. Lat /\ X e. ( Base ` K ) /\ W e. ( Base ` K ) ) -> ( X ( meet ` K ) W ) e. ( Base ` K ) )
20	18, 6, 8, 19	syl3anc 1326	. . . . . . . . 9 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( X ( meet ` K ) W ) e. ( Base ` K ) )
21	3, 9, 10, 11	oldmm2 34505	. . . . . . . . 9 |- ( ( K e. OL /\ ( X ( meet ` K ) W ) e. ( Base ` K ) /\ W e. ( Base ` K ) ) -> ( ( oc ` K ) ` ( ( ( oc ` K ) ` ( X ( meet ` K ) W ) ) ( meet ` K ) W ) ) = ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
22	2, 20, 8, 21	syl3anc 1326	. . . . . . . 8 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( oc ` K ) ` ( ( ( oc ` K ) ` ( X ( meet ` K ) W ) ) ( meet ` K ) W ) ) = ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
23	16, 22	eqtrd 2656	. . . . . . 7 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) = ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
24	23	oveq1d 6665	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) = ( ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
25		hlop 34649	. . . . . . . . . 10 |- ( K e. HL -> K e. OP )
26	25	ad2antrr 762	. . . . . . . . 9 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> K e. OP )
27	3, 11	opoccl 34481	. . . . . . . . 9 |- ( ( K e. OP /\ W e. ( Base ` K ) ) -> ( ( oc ` K ) ` W ) e. ( Base ` K ) )
28	26, 8, 27	syl2anc 693	. . . . . . . 8 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( oc ` K ) ` W ) e. ( Base ` K ) )
29	3, 9	latjass 17095	. . . . . . . 8 |- ( ( K e. Lat /\ ( ( X ( meet ` K ) W ) e. ( Base ` K ) /\ ( ( oc ` K ) ` W ) e. ( Base ` K ) /\ ( ( oc ` K ) ` W ) e. ( Base ` K ) ) ) -> ( ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) = ( ( X ( meet ` K ) W ) ( join ` K ) ( ( ( oc ` K ) ` W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ) )
30	18, 20, 28, 28, 29	syl13anc 1328	. . . . . . 7 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) = ( ( X ( meet ` K ) W ) ( join ` K ) ( ( ( oc ` K ) ` W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ) )
31	3, 9	latjidm 17074	. . . . . . . . 9 |- ( ( K e. Lat /\ ( ( oc ` K ) ` W ) e. ( Base ` K ) ) -> ( ( ( oc ` K ) ` W ) ( join ` K ) ( ( oc ` K ) ` W ) ) = ( ( oc ` K ) ` W ) )
32	18, 28, 31	syl2anc 693	. . . . . . . 8 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( oc ` K ) ` W ) ( join ` K ) ( ( oc ` K ) ` W ) ) = ( ( oc ` K ) ` W ) )
33	32	oveq2d 6666	. . . . . . 7 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( X ( meet ` K ) W ) ( join ` K ) ( ( ( oc ` K ) ` W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ) = ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
34	30, 33	eqtrd 2656	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) = ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
35	24, 34	eqtrd 2656	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) = ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) )
36	35	oveq1d 6665	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) = ( ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) )
37		hloml 34644	. . . . . 6 |- ( K e. HL -> K e. OML )
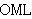38	37	ad2antrr 762	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> K e. OML )
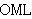39		eqid 2622	. . . . . . 7 |- ( le ` K ) = ( le ` K )
40	3, 39, 10	latmle2 17077	. . . . . 6 |- ( ( K e. Lat /\ X e. ( Base ` K ) /\ W e. ( Base ` K ) ) -> ( X ( meet ` K ) W ) ( le ` K ) W )
41	18, 6, 8, 40	syl3anc 1326	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( X ( meet ` K ) W ) ( le ` K ) W )
42	3, 39, 9, 10, 11	omlspjN 34548	. . . . 5 |- ( ( K e. OML /\ ( ( X ( meet ` K ) W ) e. ( Base ` K ) /\ W e. ( Base ` K ) ) /\ ( X ( meet ` K ) W ) ( le ` K ) W ) -> ( ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) = ( X ( meet ` K ) W ) )
43	38, 20, 8, 41, 42	syl121anc 1331	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( X ( meet ` K ) W ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) = ( X ( meet ` K ) W ) )
44	39, 4, 5	diadmleN 36327	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> X ( le ` K ) W )
45	3, 39, 10	latleeqm1 17079	. . . . . 6 |- ( ( K e. Lat /\ X e. ( Base ` K ) /\ W e. ( Base ` K ) ) -> ( X ( le ` K ) W <-> ( X ( meet ` K ) W ) = X ) )
46	18, 6, 8, 45	syl3anc 1326	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( X ( le ` K ) W <-> ( X ( meet ` K ) W ) = X ) )
47	44, 46	mpbid 222	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( X ( meet ` K ) W ) = X )
48	36, 43, 47	3eqtrrd 2661	. . 3 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> X = ( ( ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) )
49	48	fveq2d 6195	. 2 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( I ` X ) = ( I ` ( ( ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) )
50	3, 11	opoccl 34481	. . . . . . 7 |- ( ( K e. OP /\ X e. ( Base ` K ) ) -> ( ( oc ` K ) ` X ) e. ( Base ` K ) )
51	26, 6, 50	syl2anc 693	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( oc ` K ) ` X ) e. ( Base ` K ) )
52	3, 9	latjcl 17051	. . . . . 6 |- ( ( K e. Lat /\ ( ( oc ` K ) ` X ) e. ( Base ` K ) /\ ( ( oc ` K ) ` W ) e. ( Base ` K ) ) -> ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) e. ( Base ` K ) )
53	18, 51, 28, 52	syl3anc 1326	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) e. ( Base ` K ) )
54	3, 10	latmcl 17052	. . . . 5 |- ( ( K e. Lat /\ ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) e. ( Base ` K ) /\ W e. ( Base ` K ) ) -> ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) e. ( Base ` K ) )
55	18, 53, 8, 54	syl3anc 1326	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) e. ( Base ` K ) )
56	3, 39, 10	latmle2 17077	. . . . 5 |- ( ( K e. Lat /\ ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) e. ( Base ` K ) /\ W e. ( Base ` K ) ) -> ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ( le ` K ) W )
57	18, 53, 8, 56	syl3anc 1326	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ( le ` K ) W )
58	3, 39, 4, 5	diaeldm 36325	. . . . 5 |- ( ( K e. HL /\ W e. H ) -> ( ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) e. dom I <-> ( ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) e. ( Base ` K ) /\ ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ( le ` K ) W ) ) )
59	58	adantr 481	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) e. dom I <-> ( ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) e. ( Base ` K ) /\ ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ( le ` K ) W ) ) )
60	55, 57, 59	mpbir2and 957	. . 3 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) e. dom I )
61		eqid 2622	. . . 4 |- ( ( LTrn ` K ) ` W ) = ( ( LTrn ` K ) ` W )
62		doca2.n	. . . 4 |- ._|_ = ( ( ocA ` K ) ` W )
63	9, 10, 11, 4, 61, 5, 62	diaocN 36414	. . 3 |- ( ( ( K e. HL /\ W e. H ) /\ ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) e. dom I ) -> ( I ` ( ( ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) = ( ._|_ ` ( I ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ) )
64	60, 63	syldan 487	. 2 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( I ` ( ( ( ( oc ` K ) ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) = ( ._|_ ` ( I ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ) )
65	9, 10, 11, 4, 61, 5, 62	diaocN 36414	. . 3 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( I ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) = ( ._|_ ` ( I ` X ) ) )
66	65	fveq2d 6195	. 2 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ._|_ ` ( I ` ( ( ( ( oc ` K ) ` X ) ( join ` K ) ( ( oc ` K ) ` W ) ) ( meet ` K ) W ) ) ) = ( ._|_ ` ( ._|_ ` ( I ` X ) ) ) )
67	49, 64, 66	3eqtrrd 2661	1 |- ( ( ( K e. HL /\ W e. H ) /\ X e. dom I ) -> ( ._|_ ` ( ._|_ ` ( I ` X ) ) ) = ( I ` X ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   e. wcel 1990   class class class wbr 4653   dom cdm 5114   ` cfv 5888  (class class class)co 6650   Basecbs 15857   lecple 15948   occoc 15949   joincjn 16944   meetcmee 16945   Latclat 17045   OPcops 34459   OLcol 34461   OMLcoml 34462   HLchlt 34637   LHypclh 35270   LTrncltrn 35387   DIsoAcdia 36317   ocAcocaN 36408

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-riotaBAD 34239

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-1st 7168  df-2nd 7169  df-undef 7399  df-map 7859  df-preset 16928  df-poset 16946  df-plt 16958  df-lub 16974  df-glb 16975  df-join 16976  df-meet 16977  df-p0 17039  df-p1 17040  df-lat 17046  df-clat 17108  df-oposet 34463  df-cmtN 34464  df-ol 34465  df-oml 34466  df-covers 34553  df-ats 34554  df-atl 34585  df-cvlat 34609  df-hlat 34638  df-llines 34784  df-lplanes 34785  df-lvols 34786  df-lines 34787  df-psubsp 34789  df-pmap 34790  df-padd 35082  df-lhyp 35274  df-laut 35275  df-ldil 35390  df-ltrn 35391  df-trl 35446  df-disoa 36318  df-docaN 36409

This theorem is referenced by:  doca3N  36416