| Step | Hyp | Ref
| Expression |
|---|
| 1 | | crngorngo 33799 |
. . . 4
    CRingOps CRingOps      |
| 2 | | ispridlc.1 |
. . . . 5
        |
| 3 | | ispridlc.2 |
. . . . 5
        |
| 4 | | ispridlc.3 |
. . . . 5
     |
| 5 | 2, 3, 4 | ispridl 33833 |
. . . 4
          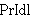                                      
   
       
             |
| 6 | 1, 5 | syl 17 |
. . 3
    CRingOps CRingOps      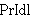                                      
   
       
             |
| 7 | | snssi 4339 |
. . . . . . . . . . . . 13
         
  |
| 8 | 2, 4 | igenidl 33862 |
. . . . . . . . . . . . 13
             
              |
| 9 | 1, 7, 8 | syl2an 494 |
. . . . . . . . . . . 12
     CRingOps CRingOps
                    |
| 10 | 9 | adantrr 753 |
. . . . . . . . . . 11
     CRingOps CRingOps
       
   
              |
| 11 | | snssi 4339 |
. . . . . . . . . . . . 13
         
  |
| 12 | 2, 4 | igenidl 33862 |
. . . . . . . . . . . . 13
             
              |
| 13 | 1, 11, 12 | syl2an 494 |
. . . . . . . . . . . 12
     CRingOps CRingOps
                    |
| 14 | 13 | adantrl 752 |
. . . . . . . . . . 11
     CRingOps CRingOps
       
   
              |
| 15 | | raleq 3138 |
. . . . . . . . . . . . 13
                                                    |
| 16 | | sseq1 3626 |
. . . . . . . . . . . . . 14
                        
   |
| 17 | 16 | orbi1d 739 |
. . . . . . . . . . . . 13
                 
    
        
        |
| 18 | 15, 17 | imbi12d 334 |
. . . . . . . . . . . 12
                 
   
       
          
   
                             
       |
| 19 | | raleq 3138 |
. . . . . . . . . . . . . 14
                                            |
| 20 | 19 | ralbidv 2986 |
. . . . . . . . . . . . 13
                          
                                     |
| 21 | | sseq1 3626 |
. . . . . . . . . . . . . 14
                        
   |
| 22 | 21 | orbi2d 738 |
. . . . . . . . . . . . 13
                            
        
   
          |
| 23 | 20, 22 | imbi12d 334 |
. . . . . . . . . . . 12
                           
       
        
                                    
        
   
           |
| 24 | 18, 23 | rspc2v 3322 |
. . . . . . . . . . 11
                                  
        
        
   
           
                                    
        
   
           |
| 25 | 10, 14, 24 | syl2anc 693 |
. . . . . . . . . 10
     CRingOps CRingOps
       
   
   
                 
   
       
                                       
        
   
           |
| 26 | 25 | adantlr 751 |
. . . . . . . . 9
      CRingOps CRingOps                 
   
   
                 
   
       
                                       
        
   
           |
| 27 | 2, 3, 4 | prnc 33866 |
. . . . . . . . . . . . . . . . . . 19
     CRingOps CRingOps
                 
   
          |
| 28 | | df-rab 2921 |
. . . . . . . . . . . . . . . . . . 19
    
   
           
                   |
| 29 | 27, 28 | syl6eq 2672 |
. . . . . . . . . . . . . . . . . 18
     CRingOps CRingOps
                         
          |
| 30 | 29 | abeq2d 2734 |
. . . . . . . . . . . . . . . . 17
     CRingOps CRingOps
                           
        |
| 31 | 30 | adantrr 753 |
. . . . . . . . . . . . . . . 16
     CRingOps CRingOps
       
   
          
   
    
          |
| 32 | 2, 3, 4 | prnc 33866 |
. . . . . . . . . . . . . . . . . . 19
     CRingOps CRingOps
                     
          |
| 33 | | df-rab 2921 |
. . . . . . . . . . . . . . . . . . 19
        
                               |
| 34 | 32, 33 | syl6eq 2672 |
. . . . . . . . . . . . . . . . . 18
     CRingOps CRingOps
                         
          |
| 35 | 34 | abeq2d 2734 |
. . . . . . . . . . . . . . . . 17
     CRingOps CRingOps
                           
        |
| 36 | 35 | adantrl 752 |
. . . . . . . . . . . . . . . 16
     CRingOps CRingOps
       
   
          
   
    
          |
| 37 | 31, 36 | anbi12d 747 |
. . . . . . . . . . . . . . 15
     CRingOps CRingOps
       
   
                      
                             
         |
| 38 | 37 | adantlr 751 |
. . . . . . . . . . . . . 14
      CRingOps CRingOps                 
   
                      
                             
         |
| 39 | 38 | adantr 481 |
. . . . . . . . . . . . 13
       CRingOps CRingOps                
                                    
                             
         |
| 40 | | reeanv 3107 |
. . . . . . . . . . . . . . . 16
        
           
                                 |
| 41 | 40 | anbi2i 730 |
. . . . . . . . . . . . . . 15
        
   
   
   
                                
   
                    |
| 42 | | an4 865 |
. . . . . . . . . . . . . . 15
        
   
   
           
                    
                            |
| 43 | 41, 42 | bitri 264 |
. . . . . . . . . . . . . 14
        
   
   
   
                            
                            |
| 44 | 2, 3, 4 | crngm4 33802 |
. . . . . . . . . . . . . . . . . . . . . 22
     CRingOps CRingOps
       
        
                                 |
| 45 | 44 | 3com23 1271 |
. . . . . . . . . . . . . . . . . . . . 21
     CRingOps CRingOps
       
        
                                 |
| 46 | 45 | 3expa 1265 |
. . . . . . . . . . . . . . . . . . . 20
      CRingOps CRingOps        
   
   
                                   |
| 47 | 46 | adantllr 755 |
. . . . . . . . . . . . . . . . . . 19
       CRingOps CRingOps                
           
   
                            |
| 48 | 47 | adantlr 751 |
. . . . . . . . . . . . . . . . . 18
        CRingOps CRingOps                                                                      |
| 49 | 2, 3, 4 | rngocl 33700 |
. . . . . . . . . . . . . . . . . . . . . . . 24
         
              |
| 50 | 1, 49 | syl3an1 1359 |
. . . . . . . . . . . . . . . . . . . . . . 23
     CRingOps CRingOps
   
              |
| 51 | 50 | 3expb 1266 |
. . . . . . . . . . . . . . . . . . . . . 22
     CRingOps CRingOps
       
   
        |
| 52 | 51 | adantlr 751 |
. . . . . . . . . . . . . . . . . . . . 21
      CRingOps CRingOps                 
   
        |
| 53 | 52 | adantlr 751 |
. . . . . . . . . . . . . . . . . . . 20
       CRingOps CRingOps                                       |
| 54 | 2, 3, 4 | idllmulcl 33819 |
. . . . . . . . . . . . . . . . . . . . . 22
         
                         
                |
| 55 | 1, 54 | sylanl1 682 |
. . . . . . . . . . . . . . . . . . . . 21
      CRingOps CRingOps                             
                |
| 56 | 55 | anassrs 680 |
. . . . . . . . . . . . . . . . . . . 20
       CRingOps CRingOps                            
                |
| 57 | 53, 56 | syldan 487 |
. . . . . . . . . . . . . . . . . . 19
       CRingOps CRingOps                                               |
| 58 | 57 | adantllr 755 |
. . . . . . . . . . . . . . . . . 18
        CRingOps CRingOps                                                          |
| 59 | 48, 58 | eqeltrrd 2702 |
. . . . . . . . . . . . . . . . 17
        CRingOps CRingOps                                                          |
| 60 | | oveq12 6659 |
. . . . . . . . . . . . . . . . . 18
            
                           |
| 61 | 60 | eleq1d 2686 |
. . . . . . . . . . . . . . . . 17
            
                                 |
| 62 | 59, 61 | syl5ibrcom 237 |
. . . . . . . . . . . . . . . 16
        CRingOps CRingOps                                                                      |
| 63 | 62 | rexlimdvva 3038 |
. . . . . . . . . . . . . . 15
       CRingOps CRingOps                
                                                  |
| 64 | 63 | adantld 483 |
. . . . . . . . . . . . . 14
       CRingOps CRingOps                
                            
   
           
       
         |
| 65 | 43, 64 | syl5bir 233 |
. . . . . . . . . . . . 13
       CRingOps CRingOps                
                       
                    
       
         |
| 66 | 39, 65 | sylbid 230 |
. . . . . . . . . . . 12
       CRingOps CRingOps                
                                              |
| 67 | 66 | ralrimivv 2970 |
. . . . . . . . . . 11
       CRingOps CRingOps                
               
                          |
| 68 | 67 | ex 450 |
. . . . . . . . . 10
      CRingOps CRingOps                 
   
                                      |
| 69 | 2, 4 | igenss 33861 |
. . . . . . . . . . . . . . . 16
             
            |
| 70 | 1, 7, 69 | syl2an 494 |
. . . . . . . . . . . . . . 15
     CRingOps CRingOps
         
        |
| 71 | | vex 3203 |
. . . . . . . . . . . . . . . 16
    |
| 72 | 71 | snss 4316 |
. . . . . . . . . . . . . . 15
           
            |
| 73 | 70, 72 | sylibr 224 |
. . . . . . . . . . . . . 14
     CRingOps CRingOps
                |
| 74 | 73 | adantrr 753 |
. . . . . . . . . . . . 13
     CRingOps CRingOps
       
   
   
      |
| 75 | | ssel 3597 |
. . . . . . . . . . . . 13
         
                  |
| 76 | 74, 75 | syl5com 31 |
. . . . . . . . . . . 12
     CRingOps CRingOps
       
   
        
       |
| 77 | 2, 4 | igenss 33861 |
. . . . . . . . . . . . . . . 16
             
            |
| 78 | 1, 11, 77 | syl2an 494 |
. . . . . . . . . . . . . . 15
     CRingOps CRingOps
         
        |
| 79 | | vex 3203 |
. . . . . . . . . . . . . . . 16
    |
| 80 | 79 | snss 4316 |
. . . . . . . . . . . . . . 15
           
            |
| 81 | 78, 80 | sylibr 224 |
. . . . . . . . . . . . . 14
     CRingOps CRingOps
                |
| 82 | 81 | adantrl 752 |
. . . . . . . . . . . . 13
     CRingOps CRingOps
       
   
   
      |
| 83 | | ssel 3597 |
. . . . . . . . . . . . 13
         
                  |
| 84 | 82, 83 | syl5com 31 |
. . . . . . . . . . . 12
     CRingOps CRingOps
       
   
        
       |
| 85 | 76, 84 | orim12d 883 |
. . . . . . . . . . 11
     CRingOps CRingOps
       
   
                      
   
       |
| 86 | 85 | adantlr 751 |
. . . . . . . . . 10
      CRingOps CRingOps                 
   
                      
   
       |
| 87 | 68, 86 | imim12d 81 |
. . . . . . . . 9
      CRingOps CRingOps                 
   
   
                         
        
   
                        
      |
| 88 | 26, 87 | syld 47 |
. . . . . . . 8
      CRingOps CRingOps                 
   
   
                 
   
       
                         
      |
| 89 | 88 | ralrimdvva 2974 |
. . . . . . 7
     CRingOps CRingOps
            
        
        
   
           
             
                
      |
| 90 | 89 | ex 450 |
. . . . . 6
    CRingOps CRingOps          
   
                 
   
       
            
   
                
       |
| 91 | 90 | adantrd 484 |
. . . . 5
    CRingOps CRingOps           
    
   
                 
   
       
            
   
                
       |
| 92 | 91 | imdistand 728 |
. . . 4
    CRingOps CRingOps                    
                 
   
       
                     
        
   
               
      |
| 93 | | df-3an 1039 |
. . . 4
                                   
   
       
                     
                         
   
       
            |
| 94 | | df-3an 1039 |
. . . 4
                  
   
               
    
   
             
   
               
      |
| 95 | 92, 93, 94 | 3imtr4g 285 |
. . 3
    CRingOps CRingOps           
                        
   
       
                    
                    
   
         |
| 96 | 6, 95 | sylbid 230 |
. 2
    CRingOps CRingOps      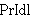                       
                
       |
| 97 | 2, 3, 4 | ispridl2 33837 |
. . . 4
         
             
   
               
       
 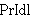     |
| 98 | 97 | ex 450 |
. . 3
               
                    
   
           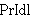      |
| 99 | 1, 98 | syl 17 |
. 2
    CRingOps CRingOps           
                    
   
           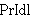      |
| 100 | 96, 99 | impbid 202 |
1
    CRingOps CRingOps      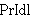                     
   
               
      |