Proof of Theorem isdmn3
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | isdmn2 33854 |
. 2
    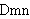 
   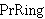 
  CRingOps CRingOps  |
| 2 | | isdmn3.1 |
. . . . . 6
        |
| 3 | | isdmn3.4 |
. . . . . 6
    GId GId   |
| 4 | 2, 3 | isprrngo 33849 |
. . . . 5
    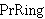            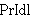      |
| 5 | | isdmn3.2 |
. . . . . . 7
        |
| 6 | | isdmn3.3 |
. . . . . . 7
     |
| 7 | 2, 5, 6 | ispridlc 33869 |
. . . . . 6
    CRingOps CRingOps      
 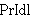    
   
                  
           
        
         |
| 8 | | crngorngo 33799 |
. . . . . . 7
    CRingOps CRingOps      |
| 9 | 8 | biantrurd 529 |
. . . . . 6
    CRingOps CRingOps      
 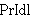    
    
   
 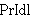       |
| 10 | | 3anass 1042 |
. . . . . . 7
                      
   
                
         
   
                                       
          |
| 11 | 2, 3 | 0idl 33824 |
. . . . . . . . . 10
                |
| 12 | 8, 11 | syl 17 |
. . . . . . . . 9
    CRingOps CRingOps            |
| 13 | 12 | biantrurd 529 |
. . . . . . . 8
    CRingOps CRingOps               
           
        
                  
   
        
           
        
          |
| 14 | 2 | rneqi 5352 |
. . . . . . . . . . . . . . 15
          |
| 15 | 6, 14 | eqtri 2644 |
. . . . . . . . . . . . . 14
         |
| 16 | | isdmn3.5 |
. . . . . . . . . . . . . 14
    GId GId   |
| 17 | 15, 5, 16 | rngo1cl 33738 |
. . . . . . . . . . . . 13
          |
| 18 | | eleq2 2690 |
. . . . . . . . . . . . . 14
              
     |
| 19 | | elsni 4194 |
. . . . . . . . . . . . . 14
            |
| 20 | 18, 19 | syl6bir 244 |
. . . . . . . . . . . . 13
            
     |
| 21 | 17, 20 | syl5com 31 |
. . . . . . . . . . . 12
          
       |
| 22 | 2, 5, 3, 16, 6 | rngoueqz 33739 |
. . . . . . . . . . . . 13
                |
| 23 | 2, 6, 3 | rngo0cl 33718 |
. . . . . . . . . . . . . 14
          |
| 24 | | en1eqsn 8190 |
. . . . . . . . . . . . . . . 16
             
    |
| 25 | 24 | eqcomd 2628 |
. . . . . . . . . . . . . . 15
                  |
| 26 | 25 | ex 450 |
. . . . . . . . . . . . . 14
              
   |
| 27 | 23, 26 | syl 17 |
. . . . . . . . . . . . 13
                  |
| 28 | 22, 27 | sylbird 250 |
. . . . . . . . . . . 12
          
   
   |
| 29 | 21, 28 | impbid 202 |
. . . . . . . . . . 11
          
 
     |
| 30 | 8, 29 | syl 17 |
. . . . . . . . . 10
    CRingOps CRingOps      
 
     |
| 31 | 30 | necon3bid 2838 |
. . . . . . . . 9
    CRingOps CRingOps        
     |
| 32 | | ovex 6678 |
. . . . . . . . . . . . 13
        |
| 33 | 32 | elsn 4192 |
. . . . . . . . . . . 12
                    |
| 34 | | velsn 4193 |
. . . . . . . . . . . . 13
            |
| 35 | | velsn 4193 |
. . . . . . . . . . . . 13
            |
| 36 | 34, 35 | orbi12i 543 |
. . . . . . . . . . . 12
        
      
   
      |
| 37 | 33, 36 | imbi12i 340 |
. . . . . . . . . . 11
                     
     
               
    |
| 38 | 37 | a1i 11 |
. . . . . . . . . 10
    CRingOps CRingOps                   
                 
   
        |
| 39 | 38 | 2ralbidv 2989 |
. . . . . . . . 9
    CRingOps CRingOps      
   
                
              
                       |
| 40 | 31, 39 | anbi12d 747 |
. . . . . . . 8
    CRingOps CRingOps               
           
        
                  
                        |
| 41 | 13, 40 | bitr3d 270 |
. . . . . . 7
    CRingOps CRingOps                       
   
                    
            
   
   
               
      |
| 42 | 10, 41 | syl5bb 272 |
. . . . . 6
    CRingOps CRingOps                       
   
                
         
        
   
               
      |
| 43 | 7, 9, 42 | 3bitr3d 298 |
. . . . 5
    CRingOps CRingOps       
   
 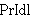     
        
   
               
      |
| 44 | 4, 43 | syl5bb 272 |
. . . 4
    CRingOps CRingOps                 
                        |
| 45 | 44 | pm5.32i 669 |
. . 3
     CRingOps CRingOps
    CRingOps CRingOps            
                        |
| 46 | | ancom 466 |
. . 3
         CRingOps CRingOps     CRingOps CRingOps       |
| 47 | | 3anass 1042 |
. . 3
     CRingOps CRingOps
    
   
   
               
    
   CRingOps CRingOps      
   
   
               
      |
| 48 | 45, 46, 47 | 3bitr4i 292 |
. 2
     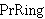    CRingOps CRingOps     CRingOps CRingOps            
                      |
| 49 | 1, 48 | bitri 264 |
1
    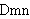 
   CRingOps CRingOps           
                       |