2llnjaN - Mathbox for Norm Megill

	Mathbox for Norm Megill		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > 2llnjaN		Structured version Visualization version Unicode version

Theorem 2llnjaN 34852

Description: The join of two different lattice lines in a lattice plane equals the plane (version of 2llnjN 34853 in terms of atoms). (Contributed by NM, 5-Jul-2012.) (New usage is discouraged.)

**Hypotheses**
Ref	Expression
2llnja.l
2llnja.j	$.\/$
2llnja.a
2llnja.n
2llnja.p

**Assertion**
Ref	Expression
2llnjaN	$/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$

**Proof of Theorem 2llnjaN**
Step	Hyp	Ref	Expression
1		eqid 2622	. 2
2		2llnja.l	. 2
3		simpl1l 1112	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
4		hllat 34650	. . 3
5	3, 4	syl 17	. 2 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
6		simpl21 1139	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
7		simpl22 1140	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
8		2llnja.j	. . . . 5 $.\/$
9		2llnja.a	. . . . 5
10	1, 8, 9	hlatjcl 34653	. . . 4 $/\$ $/\$ $.\/$
11	3, 6, 7, 10	syl3anc 1326	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
12		simpl31 1142	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
13		simpl32 1143	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
14	1, 8, 9	hlatjcl 34653	. . . 4 $/\$ $/\$ $.\/$
15	3, 12, 13, 14	syl3anc 1326	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
16	1, 8	latjcl 17051	. . 3 $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
17	5, 11, 15, 16	syl3anc 1326	. 2 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
18		simpl1r 1113	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
19		2llnja.p	. . . 4
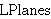20	1, 19	lplnbase 34820	. . 3
21	18, 20	syl 17	. 2 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
22		simpr1 1067	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
23		simpr2 1068	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
24	1, 2, 8	latjle12 17062	. . . 4 $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
25	5, 11, 15, 21, 24	syl13anc 1328	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
26	22, 23, 25	mpbi2and 956	. 2 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
27	1, 9	atbase 34576	. . . . . . . . . 10
28	13, 27	syl 17	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
29	1, 8	latjcl 17051	. . . . . . . . 9 $/\$ $.\/$ $/\$ $.\/$ $.\/$
30	5, 11, 28, 29	syl3anc 1326	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
31	1, 9	atbase 34576	. . . . . . . . . . 11
32	12, 31	syl 17	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
33	1, 2, 8	latlej2 17061	. . . . . . . . . 10 $/\$ $/\$ $.\/$
34	5, 32, 28, 33	syl3anc 1326	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
35	1, 2, 8	latjlej2 17066	. . . . . . . . . 10 $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
36	5, 28, 15, 11, 35	syl13anc 1328	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
37	34, 36	mpd 15	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
38	1, 2, 5, 30, 17, 21, 37, 26	lattrd 17058	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
39	38	3adant3 1081	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
40		simp11l 1172	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
41		simp121 1193	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
42		simp122 1194	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
43		simp132 1197	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
44		simp123 1195	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
45		simp23 1096	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
46		simpl3 1066	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
47		simpr 477	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$
48	1, 2, 8	latjle12 17062	. . . . . . . . . . . . . . . . 17 $/\$ $/\$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
49	5, 32, 28, 11, 48	syl13anc 1328	. . . . . . . . . . . . . . . 16 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
50	49	3adant3 1081	. . . . . . . . . . . . . . 15 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
51	50	adantr 481	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
52	46, 47, 51	mpbi2and 956	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
53		simpl3 1066	. . . . . . . . . . . . . . . 16 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $/\$
54	2, 8, 9	ps-1 34763	. . . . . . . . . . . . . . . 16 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
55	3, 53, 6, 7, 54	syl112anc 1330	. . . . . . . . . . . . . . 15 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
56	55	3adant3 1081	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
57	56	adantr 481	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
58	52, 57	mpbid 222	. . . . . . . . . . . 12 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
59	58	eqcomd 2628	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
60	59	ex 450	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
61	60	necon3ad 2807	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
62	45, 61	mpd 15	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$
63	2, 8, 9, 19	lplni2 34823	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$
64	40, 41, 42, 43, 44, 62, 63	syl132anc 1344	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
65		simp11r 1173	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
66	2, 19	lplncmp 34848	. . . . . . 7 $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
67	40, 64, 65, 66	syl3anc 1326	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
68	39, 67	mpbid 222	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
69	37	3adant3 1081	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
70	68, 69	eqbrtrrd 4677	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
71	70	3expia 1267	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
72	1, 8	latjcl 17051	. . . . . . . . 9 $/\$ $.\/$ $/\$ $.\/$ $.\/$
73	5, 11, 32, 72	syl3anc 1326	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
74	1, 2, 8	latlej1 17060	. . . . . . . . . 10 $/\$ $/\$ $.\/$
75	5, 32, 28, 74	syl3anc 1326	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
76	1, 2, 8	latjlej2 17066	. . . . . . . . . 10 $/\$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
77	5, 32, 15, 11, 76	syl13anc 1328	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
78	75, 77	mpd 15	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
79	1, 2, 5, 73, 17, 21, 78, 26	lattrd 17058	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
80	79	3adant3 1081	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
81		simp11l 1172	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
82		simp121 1193	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
83		simp122 1194	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
84		simp131 1196	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
85		simp123 1195	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
86		simp3 1063	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$
87	2, 8, 9, 19	lplni2 34823	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $.\/$ $.\/$
88	81, 82, 83, 84, 85, 86, 87	syl132anc 1344	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
89		simp11r 1173	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$
90	2, 19	lplncmp 34848	. . . . . . 7 $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
91	81, 88, 89, 90	syl3anc 1326	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
92	80, 91	mpbid 222	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$
93	78	3adant3 1081	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
94	92, 93	eqbrtrrd 4677	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$
95	94	3expia 1267	. . 3 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
96	71, 95	pm2.61d 170	. 2 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$
97	1, 2, 5, 17, 21, 26, 96	latasymd 17057	1 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $.\/$ $/\$ $.\/$ $/\$ $.\/$ $.\/$ $.\/$ $.\/$ $.\/$

Colors of variables: wff setvar class

Syntax hints:

wn 3

wi 4

wb 196 $/\$ wa 384 $/\$ w3a 1037

wceq 1483

wcel 1990

wne 2794 class class class wbr 4653

cfv 5888 (class class class)co 6650

cbs 15857

cple 15948

cjn 16944

clat 17045

catm 34550

chlt 34637

clln 34777

clpl 34778

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-ral 2917 df-rex 2918 df-reu 2919 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-preset 16928 df-poset 16946 df-plt 16958 df-lub 16974 df-glb 16975 df-join 16976 df-meet 16977 df-p0 17039 df-lat 17046 df-clat 17108 df-oposet 34463 df-ol 34465 df-oml 34466 df-covers 34553 df-ats 34554 df-atl 34585 df-cvlat 34609 df-hlat 34638 df-llines 34784 df-lplanes 34785

This theorem is referenced by: 2llnjN 34853

W3C validator