rngoisocnv - Mathbox for Jeff Madsen

	Mathbox for Jeff Madsen		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > rngoisocnv		Structured version Visualization version Unicode version

Theorem rngoisocnv 33780

Description: The inverse of a ring isomorphism is a ring isomorphism. (Contributed by Jeff Madsen, 16-Jun-2011.)

**Assertion**
Ref	Expression
rngoisocnv	$/\$ $/\$

Proof of Theorem rngoisocnv Dummy variables

are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		f1ocnv 6149	. . . . . . . 8
2		f1of 6137	. . . . . . . 8
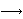3	1, 2	syl 17	. . . . . . 7
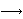
4	3	ad2antll 765	. . . . . 6 $/\$ $/\$ $/\$
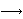5		eqid 2622	. . . . . . . . . 10
6		eqid 2622	. . . . . . . . . 10 GId GId
7		eqid 2622	. . . . . . . . . 10
8		eqid 2622	. . . . . . . . . 10 GId GId
9	5, 6, 7, 8	rngohom1 33767	. . . . . . . . 9 $/\$ $/\$ GId GId
10	9	3expa 1265	. . . . . . . 8 $/\$ $/\$ GId GId
11	10	adantrr 753	. . . . . . 7 $/\$ $/\$ $/\$ GId GId
12		eqid 2622	. . . . . . . . . . 11
13	12, 5, 6	rngo1cl 33738	. . . . . . . . . 10 GId
14		f1ocnvfv 6534	. . . . . . . . . 10 $/\$ GId GId GId GId GId
15	13, 14	sylan2 491	. . . . . . . . 9 $/\$ GId GId GId GId
16	15	ancoms 469	. . . . . . . 8 $/\$ GId GId GId GId
17	16	ad2ant2rl 785	. . . . . . 7 $/\$ $/\$ $/\$ GId GId GId GId
18	11, 17	mpd 15	. . . . . 6 $/\$ $/\$ $/\$ GId GId
19		f1ocnvfv2 6533	. . . . . . . . . . . . . 14 $/\$
20		f1ocnvfv2 6533	. . . . . . . . . . . . . 14 $/\$
21	19, 20	anim12da 33506	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
22		oveq12 6659	. . . . . . . . . . . . 13 $/\$
23	21, 22	syl 17	. . . . . . . . . . . 12 $/\$ $/\$
24	23	adantll 750	. . . . . . . . . . 11 $/\$ $/\$ $/\$
25	24	adantll 750	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$
26		f1ocnvdm 6540	. . . . . . . . . . . . . . . 16 $/\$
27		f1ocnvdm 6540	. . . . . . . . . . . . . . . 16 $/\$
28	26, 27	anim12da 33506	. . . . . . . . . . . . . . 15 $/\$ $/\$ $/\$
29		eqid 2622	. . . . . . . . . . . . . . . 16
30		eqid 2622	. . . . . . . . . . . . . . . 16
31	29, 12, 30	rngohomadd 33768	. . . . . . . . . . . . . . 15 $/\$ $/\$ $/\$ $/\$
32	28, 31	sylan2 491	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$ $/\$ $/\$
33	32	exp32 631	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
34	33	3expa 1265	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
35	34	impr 649	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
36	35	imp 445	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$
37		eqid 2622	. . . . . . . . . . . . . . . 16
38	30, 37	rngogcl 33711	. . . . . . . . . . . . . . 15 $/\$ $/\$
39	38	3expb 1266	. . . . . . . . . . . . . 14 $/\$ $/\$
40		f1ocnvfv2 6533	. . . . . . . . . . . . . . 15 $/\$
41	40	ancoms 469	. . . . . . . . . . . . . 14 $/\$
42	39, 41	sylan 488	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
43	42	an32s 846	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
44	43	adantlll 754	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
45	44	adantlrl 756	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$
46	25, 36, 45	3eqtr4rd 2667	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$
47		f1of1 6136	. . . . . . . . . . . 12
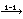48	47	ad2antlr 763	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
49		f1ocnvdm 6540	. . . . . . . . . . . . . . 15 $/\$
50	49	ancoms 469	. . . . . . . . . . . . . 14 $/\$
51	39, 50	sylan 488	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
52	51	an32s 846	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
53	52	adantlll 754	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
54	29, 12	rngogcl 33711	. . . . . . . . . . . . . . 15 $/\$ $/\$
55	54	3expb 1266	. . . . . . . . . . . . . 14 $/\$ $/\$
56	28, 55	sylan2 491	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
57	56	anassrs 680	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
58	57	adantllr 755	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
59		f1fveq 6519	. . . . . . . . . . 11 $/\$ $/\$
60	48, 53, 58, 59	syl12anc 1324	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$
61	60	adantlrl 756	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$
62	46, 61	mpbid 222	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$
63		oveq12 6659	. . . . . . . . . . . . 13 $/\$
64	21, 63	syl 17	. . . . . . . . . . . 12 $/\$ $/\$
65	64	adantll 750	. . . . . . . . . . 11 $/\$ $/\$ $/\$
66	65	adantll 750	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$
67	29, 12, 5, 7	rngohommul 33769	. . . . . . . . . . . . . . 15 $/\$ $/\$ $/\$ $/\$
68	28, 67	sylan2 491	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$ $/\$ $/\$
69	68	exp32 631	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
70	69	3expa 1265	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
71	70	impr 649	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
72	71	imp 445	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$
73	30, 7, 37	rngocl 33700	. . . . . . . . . . . . . . 15 $/\$ $/\$
74	73	3expb 1266	. . . . . . . . . . . . . 14 $/\$ $/\$
75		f1ocnvfv2 6533	. . . . . . . . . . . . . . 15 $/\$
76	75	ancoms 469	. . . . . . . . . . . . . 14 $/\$
77	74, 76	sylan 488	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
78	77	an32s 846	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
79	78	adantlll 754	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
80	79	adantlrl 756	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$
81	66, 72, 80	3eqtr4rd 2667	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$
82		f1ocnvdm 6540	. . . . . . . . . . . . . . 15 $/\$
83	82	ancoms 469	. . . . . . . . . . . . . 14 $/\$
84	74, 83	sylan 488	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
85	84	an32s 846	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
86	85	adantlll 754	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
87	29, 5, 12	rngocl 33700	. . . . . . . . . . . . . . 15 $/\$ $/\$
88	87	3expb 1266	. . . . . . . . . . . . . 14 $/\$ $/\$
89	28, 88	sylan2 491	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
90	89	anassrs 680	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
91	90	adantllr 755	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
92		f1fveq 6519	. . . . . . . . . . 11 $/\$ $/\$
93	48, 86, 91, 92	syl12anc 1324	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$
94	93	adantlrl 756	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$
95	81, 94	mpbid 222	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$
96	62, 95	jca 554	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
97	96	ralrimivva 2971	. . . . . 6 $/\$ $/\$ $/\$ $/\$
98	30, 7, 37, 8, 29, 5, 12, 6	isrngohom 33764	. . . . . . . 8 $/\$ $/\$ GId GId $/\$ $/\$
99	98	ancoms 469	. . . . . . 7 $/\$ $/\$ GId GId $/\$ $/\$
100	99	adantr 481	. . . . . 6 $/\$ $/\$ $/\$ $/\$ GId GId $/\$ $/\$
101	4, 18, 97, 100	mpbir3and 1245	. . . . 5 $/\$ $/\$ $/\$
102	1	ad2antll 765	. . . . 5 $/\$ $/\$ $/\$
103	101, 102	jca 554	. . . 4 $/\$ $/\$ $/\$ $/\$
104	103	ex 450	. . 3 $/\$ $/\$ $/\$
105	29, 12, 30, 37	isrngoiso 33777	. . 3 $/\$ $/\$
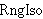
106	30, 37, 29, 12	isrngoiso 33777	. . . 4 $/\$ $/\$
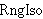
107	106	ancoms 469	. . 3 $/\$ $/\$
108	104, 105, 107	3imtr4d 283	. 2 $/\$
109	108	3impia 1261	1 $/\$ $/\$

Colors of variables: wff setvar class

Syntax hints:

wi 4

wb 196 $/\$ wa 384 $/\$ w3a 1037

wceq 1483

wcel 1990

wral 2912

ccnv 5113

crn 5115

wf 5884

wf1 5885

wf1o 5887

cfv 5888 (class class class)co 6650

c1st 7166

c2nd 7167 GIdcgi 27344

crngo 33693

crnghom 33759

crngiso 33760

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-ral 2917 df-rex 2918 df-reu 2919 df-rmo 2920 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-mpt2 6655 df-1st 7168 df-2nd 7169 df-map 7859 df-grpo 27347 df-gid 27348 df-ablo 27399 df-ass 33642 df-exid 33644 df-mgmOLD 33648 df-sgrOLD 33660 df-mndo 33666 df-rngo 33694 df-rngohom 33762 df-rngoiso 33775

This theorem is referenced by: riscer 33787

W3C validator