Theorem glbconN 34663

Description: De Morgan's law for GLB and LUB. This holds in any complete ortholattice, although we assume HL for convenience. (Contributed by NM, 17-Jan-2012.) (New usage is discouraged.)

Hypotheses

Ref	Expression
glbcon.b	|- B = ( Base ` K )
glbcon.u	|- U = ( lub ` K )
glbcon.g	|- G = ( glb ` K )
glbcon.o	|- ._|_ = ( oc ` K )

Assertion

Ref	Expression
glbconN	|- ( ( K e. HL /\ S C_ B ) -> ( G ` S ) = ( ._|_ ` ( U ` { x e. B | ( ._|_ ` x ) e. S } ) ) )

Distinct variable groups:   x, B   x, ._|_   x, S

Allowed substitution hints:   U( x)   G( x)   K( x)

Proof of Theorem glbconN

Dummy variables u t v w y z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		dfin5 3582	. . . 4 |- ( B i^i S ) = { x e. B | x e. S }
2		sseqin2 3817	. . . . 5 |- ( S C_ B <-> ( B i^i S ) = S )
3	2	biimpi 206	. . . 4 |- ( S C_ B -> ( B i^i S ) = S )
4	1, 3	syl5reqr 2671	. . 3 |- ( S C_ B -> S = { x e. B | x e. S } )
5	4	fveq2d 6195	. 2 |- ( S C_ B -> ( G ` S ) = ( G ` { x e. B | x e. S } ) )
6		glbcon.b	. . . 4 |- B = ( Base ` K )
7		eqid 2622	. . . 4 |- ( le ` K ) = ( le ` K )
8		glbcon.g	. . . 4 |- G = ( glb ` K )
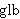9		biid 251	. . . 4 |- ( ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) <-> ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) )
10		id 22	. . . 4 |- ( K e. HL -> K e. HL )
11		ssrab2 3687	. . . . 5 |- { x e. B | x e. S } C_ B
12	11	a1i 11	. . . 4 |- ( K e. HL -> { x e. B | x e. S } C_ B )
13	6, 7, 8, 9, 10, 12	glbval 16997	. . 3 |- ( K e. HL -> ( G ` { x e. B | x e. S } ) = ( iota_ y e. B ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) ) )
14		hlop 34649	. . . 4 |- ( K e. HL -> K e. OP )
15		hlclat 34645	. . . . . . 7 |- ( K e. HL -> K e. CLat )
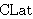16	6, 8	clatglbcl 17114	. . . . . . 7 |- ( ( K e. CLat /\ { x e. B | x e. S } C_ B ) -> ( G ` { x e. B | x e. S } ) e. B )
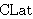
17	15, 11, 16	sylancl 694	. . . . . 6 |- ( K e. HL -> ( G ` { x e. B | x e. S } ) e. B )
18	13, 17	eqeltrrd 2702	. . . . 5 |- ( K e. HL -> ( iota_ y e. B ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) ) e. B )
19		fvex 6201	. . . . . . 7 |- ( Base ` K ) e. _V
20	6, 19	eqeltri 2697	. . . . . 6 |- B e. _V
21	20	riotaclbBAD 34241	. . . . 5 |- ( E! y e. B ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) <-> ( iota_ y e. B ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) ) e. B )
22	18, 21	sylibr 224	. . . 4 |- ( K e. HL -> E! y e. B ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) )
23		glbcon.o	. . . . 5 |- ._|_ = ( oc ` K )
24		breq1 4656	. . . . . . 7 |- ( y = ( ._|_ ` v ) -> ( y ( le ` K ) z <-> ( ._|_ ` v ) ( le ` K ) z ) )
25	24	ralbidv 2986	. . . . . 6 |- ( y = ( ._|_ ` v ) -> ( A. z e. { x e. B | x e. S } y ( le ` K ) z <-> A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z ) )
26		breq2 4657	. . . . . . . 8 |- ( y = ( ._|_ ` v ) -> ( w ( le ` K ) y <-> w ( le ` K ) ( ._|_ ` v ) ) )
27	26	imbi2d 330	. . . . . . 7 |- ( y = ( ._|_ ` v ) -> ( ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) <-> ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) )
28	27	ralbidv 2986	. . . . . 6 |- ( y = ( ._|_ ` v ) -> ( A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) <-> A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) )
29	25, 28	anbi12d 747	. . . . 5 |- ( y = ( ._|_ ` v ) -> ( ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) <-> ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) ) )
30	6, 23, 29	riotaocN 34496	. . . 4 |- ( ( K e. OP /\ E! y e. B ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) ) -> ( iota_ y e. B ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) ) = ( ._|_ ` ( iota_ v e. B ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) ) ) )
31	14, 22, 30	syl2anc 693	. . 3 |- ( K e. HL -> ( iota_ y e. B ( A. z e. { x e. B | x e. S } y ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) y ) ) ) = ( ._|_ ` ( iota_ v e. B ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) ) ) )
32	14	ad2antrr 762	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ u e. B ) -> K e. OP )
33	6, 23	opoccl 34481	. . . . . . . . . . 11 |- ( ( K e. OP /\ u e. B ) -> ( ._|_ ` u ) e. B )
34	32, 33	sylancom 701	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ u e. B ) -> ( ._|_ ` u ) e. B )
35	14	ad2antrr 762	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ v e. B ) /\ z e. B ) -> K e. OP )
36	6, 23	opoccl 34481	. . . . . . . . . . . 12 |- ( ( K e. OP /\ z e. B ) -> ( ._|_ ` z ) e. B )
37	35, 36	sylancom 701	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ z e. B ) -> ( ._|_ ` z ) e. B )
38	6, 23	opococ 34482	. . . . . . . . . . . . 13 |- ( ( K e. OP /\ z e. B ) -> ( ._|_ ` ( ._|_ ` z ) ) = z )
39	35, 38	sylancom 701	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ v e. B ) /\ z e. B ) -> ( ._|_ ` ( ._|_ ` z ) ) = z )
40	39	eqcomd 2628	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ z e. B ) -> z = ( ._|_ ` ( ._|_ ` z ) ) )
41		fveq2 6191	. . . . . . . . . . . . 13 |- ( u = ( ._|_ ` z ) -> ( ._|_ ` u ) = ( ._|_ ` ( ._|_ ` z ) ) )
42	41	eqeq2d 2632	. . . . . . . . . . . 12 |- ( u = ( ._|_ ` z ) -> ( z = ( ._|_ ` u ) <-> z = ( ._|_ ` ( ._|_ ` z ) ) ) )
43	42	rspcev 3309	. . . . . . . . . . 11 |- ( ( ( ._|_ ` z ) e. B /\ z = ( ._|_ ` ( ._|_ ` z ) ) ) -> E. u e. B z = ( ._|_ ` u ) )
44	37, 40, 43	syl2anc 693	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ z e. B ) -> E. u e. B z = ( ._|_ ` u ) )
45		eleq1 2689	. . . . . . . . . . . 12 |- ( z = ( ._|_ ` u ) -> ( z e. S <-> ( ._|_ ` u ) e. S ) )
46		breq2 4657	. . . . . . . . . . . 12 |- ( z = ( ._|_ ` u ) -> ( ( ._|_ ` v ) ( le ` K ) z <-> ( ._|_ ` v ) ( le ` K ) ( ._|_ ` u ) ) )
47	45, 46	imbi12d 334	. . . . . . . . . . 11 |- ( z = ( ._|_ ` u ) -> ( ( z e. S -> ( ._|_ ` v ) ( le ` K ) z ) <-> ( ( ._|_ ` u ) e. S -> ( ._|_ ` v ) ( le ` K ) ( ._|_ ` u ) ) ) )
48	47	adantl 482	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ z = ( ._|_ ` u ) ) -> ( ( z e. S -> ( ._|_ ` v ) ( le ` K ) z ) <-> ( ( ._|_ ` u ) e. S -> ( ._|_ ` v ) ( le ` K ) ( ._|_ ` u ) ) ) )
49	34, 44, 48	ralxfrd 4879	. . . . . . . . 9 |- ( ( K e. HL /\ v e. B ) -> ( A. z e. B ( z e. S -> ( ._|_ ` v ) ( le ` K ) z ) <-> A. u e. B ( ( ._|_ ` u ) e. S -> ( ._|_ ` v ) ( le ` K ) ( ._|_ ` u ) ) ) )
50		simpr 477	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ v e. B ) /\ u e. B ) -> u e. B )
51		simplr 792	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ v e. B ) /\ u e. B ) -> v e. B )
52	6, 7, 23	oplecon3b 34487	. . . . . . . . . . . 12 |- ( ( K e. OP /\ u e. B /\ v e. B ) -> ( u ( le ` K ) v <-> ( ._|_ ` v ) ( le ` K ) ( ._|_ ` u ) ) )
53	32, 50, 51, 52	syl3anc 1326	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ u e. B ) -> ( u ( le ` K ) v <-> ( ._|_ ` v ) ( le ` K ) ( ._|_ ` u ) ) )
54	53	imbi2d 330	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ u e. B ) -> ( ( ( ._|_ ` u ) e. S -> u ( le ` K ) v ) <-> ( ( ._|_ ` u ) e. S -> ( ._|_ ` v ) ( le ` K ) ( ._|_ ` u ) ) ) )
55	54	ralbidva 2985	. . . . . . . . 9 |- ( ( K e. HL /\ v e. B ) -> ( A. u e. B ( ( ._|_ ` u ) e. S -> u ( le ` K ) v ) <-> A. u e. B ( ( ._|_ ` u ) e. S -> ( ._|_ ` v ) ( le ` K ) ( ._|_ ` u ) ) ) )
56	49, 55	bitr4d 271	. . . . . . . 8 |- ( ( K e. HL /\ v e. B ) -> ( A. z e. B ( z e. S -> ( ._|_ ` v ) ( le ` K ) z ) <-> A. u e. B ( ( ._|_ ` u ) e. S -> u ( le ` K ) v ) ) )
57		eleq1 2689	. . . . . . . . 9 |- ( x = z -> ( x e. S <-> z e. S ) )
58	57	ralrab 3368	. . . . . . . 8 |- ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z <-> A. z e. B ( z e. S -> ( ._|_ ` v ) ( le ` K ) z ) )
59		fveq2 6191	. . . . . . . . . 10 |- ( x = u -> ( ._|_ ` x ) = ( ._|_ ` u ) )
60	59	eleq1d 2686	. . . . . . . . 9 |- ( x = u -> ( ( ._|_ ` x ) e. S <-> ( ._|_ ` u ) e. S ) )
61	60	ralrab 3368	. . . . . . . 8 |- ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) v <-> A. u e. B ( ( ._|_ ` u ) e. S -> u ( le ` K ) v ) )
62	56, 58, 61	3bitr4g 303	. . . . . . 7 |- ( ( K e. HL /\ v e. B ) -> ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z <-> A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) v ) )
63	14	ad2antrr 762	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> K e. OP )
64	6, 23	opoccl 34481	. . . . . . . . . 10 |- ( ( K e. OP /\ t e. B ) -> ( ._|_ ` t ) e. B )
65	63, 64	sylancom 701	. . . . . . . . 9 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> ( ._|_ ` t ) e. B )
66	14	ad2antrr 762	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ w e. B ) -> K e. OP )
67	6, 23	opoccl 34481	. . . . . . . . . . 11 |- ( ( K e. OP /\ w e. B ) -> ( ._|_ ` w ) e. B )
68	66, 67	sylancom 701	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ w e. B ) -> ( ._|_ ` w ) e. B )
69	6, 23	opococ 34482	. . . . . . . . . . . 12 |- ( ( K e. OP /\ w e. B ) -> ( ._|_ ` ( ._|_ ` w ) ) = w )
70	66, 69	sylancom 701	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ w e. B ) -> ( ._|_ ` ( ._|_ ` w ) ) = w )
71	70	eqcomd 2628	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ w e. B ) -> w = ( ._|_ ` ( ._|_ ` w ) ) )
72		fveq2 6191	. . . . . . . . . . . 12 |- ( t = ( ._|_ ` w ) -> ( ._|_ ` t ) = ( ._|_ ` ( ._|_ ` w ) ) )
73	72	eqeq2d 2632	. . . . . . . . . . 11 |- ( t = ( ._|_ ` w ) -> ( w = ( ._|_ ` t ) <-> w = ( ._|_ ` ( ._|_ ` w ) ) ) )
74	73	rspcev 3309	. . . . . . . . . 10 |- ( ( ( ._|_ ` w ) e. B /\ w = ( ._|_ ` ( ._|_ ` w ) ) ) -> E. t e. B w = ( ._|_ ` t ) )
75	68, 71, 74	syl2anc 693	. . . . . . . . 9 |- ( ( ( K e. HL /\ v e. B ) /\ w e. B ) -> E. t e. B w = ( ._|_ ` t ) )
76		breq1 4656	. . . . . . . . . . . 12 |- ( w = ( ._|_ ` t ) -> ( w ( le ` K ) z <-> ( ._|_ ` t ) ( le ` K ) z ) )
77	76	ralbidv 2986	. . . . . . . . . . 11 |- ( w = ( ._|_ ` t ) -> ( A. z e. { x e. B | x e. S } w ( le ` K ) z <-> A. z e. { x e. B | x e. S } ( ._|_ ` t ) ( le ` K ) z ) )
78		breq1 4656	. . . . . . . . . . 11 |- ( w = ( ._|_ ` t ) -> ( w ( le ` K ) ( ._|_ ` v ) <-> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` v ) ) )
79	77, 78	imbi12d 334	. . . . . . . . . 10 |- ( w = ( ._|_ ` t ) -> ( ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) <-> ( A. z e. { x e. B | x e. S } ( ._|_ ` t ) ( le ` K ) z -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` v ) ) ) )
80	79	adantl 482	. . . . . . . . 9 |- ( ( ( K e. HL /\ v e. B ) /\ w = ( ._|_ ` t ) ) -> ( ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) <-> ( A. z e. { x e. B | x e. S } ( ._|_ ` t ) ( le ` K ) z -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` v ) ) ) )
81	65, 75, 80	ralxfrd 4879	. . . . . . . 8 |- ( ( K e. HL /\ v e. B ) -> ( A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) <-> A. t e. B ( A. z e. { x e. B | x e. S } ( ._|_ ` t ) ( le ` K ) z -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` v ) ) ) )
82	14	ad3antrrr 766	. . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ u e. B ) -> K e. OP )
83		simpr 477	. . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ u e. B ) -> u e. B )
84		simplr 792	. . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ u e. B ) -> t e. B )
85	6, 7, 23	oplecon3b 34487	. . . . . . . . . . . . . . 15 |- ( ( K e. OP /\ u e. B /\ t e. B ) -> ( u ( le ` K ) t <-> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` u ) ) )
86	82, 83, 84, 85	syl3anc 1326	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ u e. B ) -> ( u ( le ` K ) t <-> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` u ) ) )
87	86	imbi2d 330	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ u e. B ) -> ( ( ( ._|_ ` u ) e. S -> u ( le ` K ) t ) <-> ( ( ._|_ ` u ) e. S -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` u ) ) ) )
88	87	ralbidva 2985	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> ( A. u e. B ( ( ._|_ ` u ) e. S -> u ( le ` K ) t ) <-> A. u e. B ( ( ._|_ ` u ) e. S -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` u ) ) ) )
89	82, 33	sylancom 701	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ u e. B ) -> ( ._|_ ` u ) e. B )
90	14	ad3antrrr 766	. . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ z e. B ) -> K e. OP )
91	90, 36	sylancom 701	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ z e. B ) -> ( ._|_ ` z ) e. B )
92	90, 38	sylancom 701	. . . . . . . . . . . . . . 15 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ z e. B ) -> ( ._|_ ` ( ._|_ ` z ) ) = z )
93	92	eqcomd 2628	. . . . . . . . . . . . . 14 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ z e. B ) -> z = ( ._|_ ` ( ._|_ ` z ) ) )
94	91, 93, 43	syl2anc 693	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ z e. B ) -> E. u e. B z = ( ._|_ ` u ) )
95		breq2 4657	. . . . . . . . . . . . . . 15 |- ( z = ( ._|_ ` u ) -> ( ( ._|_ ` t ) ( le ` K ) z <-> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` u ) ) )
96	45, 95	imbi12d 334	. . . . . . . . . . . . . 14 |- ( z = ( ._|_ ` u ) -> ( ( z e. S -> ( ._|_ ` t ) ( le ` K ) z ) <-> ( ( ._|_ ` u ) e. S -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` u ) ) ) )
97	96	adantl 482	. . . . . . . . . . . . 13 |- ( ( ( ( K e. HL /\ v e. B ) /\ t e. B ) /\ z = ( ._|_ ` u ) ) -> ( ( z e. S -> ( ._|_ ` t ) ( le ` K ) z ) <-> ( ( ._|_ ` u ) e. S -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` u ) ) ) )
98	89, 94, 97	ralxfrd 4879	. . . . . . . . . . . 12 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> ( A. z e. B ( z e. S -> ( ._|_ ` t ) ( le ` K ) z ) <-> A. u e. B ( ( ._|_ ` u ) e. S -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` u ) ) ) )
99	88, 98	bitr4d 271	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> ( A. u e. B ( ( ._|_ ` u ) e. S -> u ( le ` K ) t ) <-> A. z e. B ( z e. S -> ( ._|_ ` t ) ( le ` K ) z ) ) )
100	60	ralrab 3368	. . . . . . . . . . 11 |- ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t <-> A. u e. B ( ( ._|_ ` u ) e. S -> u ( le ` K ) t ) )
101	57	ralrab 3368	. . . . . . . . . . 11 |- ( A. z e. { x e. B | x e. S } ( ._|_ ` t ) ( le ` K ) z <-> A. z e. B ( z e. S -> ( ._|_ ` t ) ( le ` K ) z ) )
102	99, 100, 101	3bitr4g 303	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t <-> A. z e. { x e. B | x e. S } ( ._|_ ` t ) ( le ` K ) z ) )
103		simplr 792	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> v e. B )
104		simpr 477	. . . . . . . . . . 11 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> t e. B )
105	6, 7, 23	oplecon3b 34487	. . . . . . . . . . 11 |- ( ( K e. OP /\ v e. B /\ t e. B ) -> ( v ( le ` K ) t <-> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` v ) ) )
106	63, 103, 104, 105	syl3anc 1326	. . . . . . . . . 10 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> ( v ( le ` K ) t <-> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` v ) ) )
107	102, 106	imbi12d 334	. . . . . . . . 9 |- ( ( ( K e. HL /\ v e. B ) /\ t e. B ) -> ( ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) <-> ( A. z e. { x e. B | x e. S } ( ._|_ ` t ) ( le ` K ) z -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` v ) ) ) )
108	107	ralbidva 2985	. . . . . . . 8 |- ( ( K e. HL /\ v e. B ) -> ( A. t e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) <-> A. t e. B ( A. z e. { x e. B | x e. S } ( ._|_ ` t ) ( le ` K ) z -> ( ._|_ ` t ) ( le ` K ) ( ._|_ ` v ) ) ) )
109	81, 108	bitr4d 271	. . . . . . 7 |- ( ( K e. HL /\ v e. B ) -> ( A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) <-> A. t e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) ) )
110	62, 109	anbi12d 747	. . . . . 6 |- ( ( K e. HL /\ v e. B ) -> ( ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) <-> ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) v /\ A. t e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) ) ) )
111	110	riotabidva 6627	. . . . 5 |- ( K e. HL -> ( iota_ v e. B ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) ) = ( iota_ v e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) v /\ A. t e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) ) ) )
112		ssrab2 3687	. . . . . 6 |- { x e. B | ( ._|_ ` x ) e. S } C_ B
113		glbcon.u	. . . . . . 7 |- U = ( lub ` K )
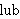114		biid 251	. . . . . . 7 |- ( ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) v /\ A. t e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) ) <-> ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) v /\ A. t e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) ) )
115		simpl 473	. . . . . . 7 |- ( ( K e. HL /\ { x e. B | ( ._|_ ` x ) e. S } C_ B ) -> K e. HL )
116		simpr 477	. . . . . . 7 |- ( ( K e. HL /\ { x e. B | ( ._|_ ` x ) e. S } C_ B ) -> { x e. B | ( ._|_ ` x ) e. S } C_ B )
117	6, 7, 113, 114, 115, 116	lubval 16984	. . . . . 6 |- ( ( K e. HL /\ { x e. B | ( ._|_ ` x ) e. S } C_ B ) -> ( U ` { x e. B | ( ._|_ ` x ) e. S } ) = ( iota_ v e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) v /\ A. t e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) ) ) )
118	112, 117	mpan2 707	. . . . 5 |- ( K e. HL -> ( U ` { x e. B | ( ._|_ ` x ) e. S } ) = ( iota_ v e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) v /\ A. t e. B ( A. u e. { x e. B | ( ._|_ ` x ) e. S } u ( le ` K ) t -> v ( le ` K ) t ) ) ) )
119	111, 118	eqtr4d 2659	. . . 4 |- ( K e. HL -> ( iota_ v e. B ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) ) = ( U ` { x e. B | ( ._|_ ` x ) e. S } ) )
120	119	fveq2d 6195	. . 3 |- ( K e. HL -> ( ._|_ ` ( iota_ v e. B ( A. z e. { x e. B | x e. S } ( ._|_ ` v ) ( le ` K ) z /\ A. w e. B ( A. z e. { x e. B | x e. S } w ( le ` K ) z -> w ( le ` K ) ( ._|_ ` v ) ) ) ) ) = ( ._|_ ` ( U ` { x e. B | ( ._|_ ` x ) e. S } ) ) )
121	13, 31, 120	3eqtrd 2660	. 2 |- ( K e. HL -> ( G ` { x e. B | x e. S } ) = ( ._|_ ` ( U ` { x e. B | ( ._|_ ` x ) e. S } ) ) )
122	5, 121	sylan9eqr 2678	1 |- ( ( K e. HL /\ S C_ B ) -> ( G ` S ) = ( ._|_ ` ( U ` { x e. B | ( ._|_ ` x ) e. S } ) ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   e. wcel 1990   A.wral 2912   E.wrex 2913   E!wreu 2914   {crab 2916   _Vcvv 3200   i^i cin 3573   C_ wss 3574   class class class wbr 4653   ` cfv 5888   iota_crio 6610   Basecbs 15857   lecple 15948   occoc 15949   lubclub 16942   glbcglb 16943   CLatccla 17107   OPcops 34459   HLchlt 34637

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-riotaBAD 34239

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-undef 7399  df-lub 16974  df-glb 16975  df-clat 17108  df-oposet 34463  df-ol 34465  df-oml 34466  df-hlat 34638

This theorem is referenced by:  glbconxN  34664