Theorem tgpt0 21922

Description: Hausdorff and T0 are equivalent for topological groups. (Contributed by Mario Carneiro, 18-Sep-2015.)

Hypothesis

Ref	Expression
tgpt1.j	|- J = ( TopOpen ` G )

Assertion

Ref	Expression
tgpt0	|- ( G e. TopGrp -> ( J e. Haus <-> J e. Kol2 ) )

Proof of Theorem tgpt0

Dummy variables w a x y z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		tgpt1.j	. . 3 |- J = ( TopOpen ` G )
2	1	tgpt1 21921	. 2 |- ( G e. TopGrp -> ( J e. Haus <-> J e. Fre ) )
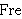3		t1t0 21152	. . 3 |- ( J e. Fre -> J e. Kol2 )
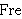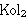4		eleq2 2690	. . . . . . . . . . . 12 |- ( w = z -> ( x e. w <-> x e. z ) )
5		eleq2 2690	. . . . . . . . . . . 12 |- ( w = z -> ( y e. w <-> y e. z ) )
6	4, 5	imbi12d 334	. . . . . . . . . . 11 |- ( w = z -> ( ( x e. w -> y e. w ) <-> ( x e. z -> y e. z ) ) )
7	6	rspccva 3308	. . . . . . . . . 10 |- ( ( A. w e. J ( x e. w -> y e. w ) /\ z e. J ) -> ( x e. z -> y e. z ) )
8	7	adantll 750	. . . . . . . . 9 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ z e. J ) -> ( x e. z -> y e. z ) )
9		tgpgrp 21882	. . . . . . . . . . . . . . 15 |- ( G e. TopGrp -> G e. Grp )
10	9	ad3antrrr 766	. . . . . . . . . . . . . 14 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> G e. Grp )
11		simpllr 799	. . . . . . . . . . . . . . 15 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) )
12	11	simprd 479	. . . . . . . . . . . . . 14 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> y e. ( Base ` G ) )
13		eqid 2622	. . . . . . . . . . . . . . 15 |- ( Base ` G ) = ( Base ` G )
14		eqid 2622	. . . . . . . . . . . . . . 15 |- ( 0g ` G ) = ( 0g ` G )
15		eqid 2622	. . . . . . . . . . . . . . 15 |- ( -g ` G ) = ( -g ` G )
16	13, 14, 15	grpsubid 17499	. . . . . . . . . . . . . 14 |- ( ( G e. Grp /\ y e. ( Base ` G ) ) -> ( y ( -g ` G ) y ) = ( 0g ` G ) )
17	10, 12, 16	syl2anc 693	. . . . . . . . . . . . 13 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( y ( -g ` G ) y ) = ( 0g ` G ) )
18	17	oveq1d 6665	. . . . . . . . . . . 12 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( ( y ( -g ` G ) y ) ( +g ` G ) x ) = ( ( 0g ` G ) ( +g ` G ) x ) )
19	11	simpld 475	. . . . . . . . . . . . 13 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> x e. ( Base ` G ) )
20		eqid 2622	. . . . . . . . . . . . . 14 |- ( +g ` G ) = ( +g ` G )
21	13, 20, 14	grplid 17452	. . . . . . . . . . . . 13 |- ( ( G e. Grp /\ x e. ( Base ` G ) ) -> ( ( 0g ` G ) ( +g ` G ) x ) = x )
22	10, 19, 21	syl2anc 693	. . . . . . . . . . . 12 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( ( 0g ` G ) ( +g ` G ) x ) = x )
23	18, 22	eqtrd 2656	. . . . . . . . . . 11 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( ( y ( -g ` G ) y ) ( +g ` G ) x ) = x )
24		tgptmd 21883	. . . . . . . . . . . . . . . 16 |- ( G e. TopGrp -> G e. TopMnd )
25	24	ad3antrrr 766	. . . . . . . . . . . . . . 15 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> G e. TopMnd )
26	1, 13	tgptopon 21886	. . . . . . . . . . . . . . . 16 |- ( G e. TopGrp -> J e. (TopOn ` ( Base ` G ) ) )
27	26	ad3antrrr 766	. . . . . . . . . . . . . . 15 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> J e. (TopOn ` ( Base ` G ) ) )
28	27, 27, 12	cnmptc 21465	. . . . . . . . . . . . . . . 16 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( a e. ( Base ` G ) |-> y ) e. ( J Cn J ) )
29	27	cnmptid 21464	. . . . . . . . . . . . . . . 16 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( a e. ( Base ` G ) |-> a ) e. ( J Cn J ) )
30	1, 15	tgpsubcn 21894	. . . . . . . . . . . . . . . . 17 |- ( G e. TopGrp -> ( -g ` G ) e. ( ( J tX J ) Cn J ) )
31	30	ad3antrrr 766	. . . . . . . . . . . . . . . 16 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( -g ` G ) e. ( ( J tX J ) Cn J ) )
32	27, 28, 29, 31	cnmpt12f 21469	. . . . . . . . . . . . . . 15 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( a e. ( Base ` G ) |-> ( y ( -g ` G ) a ) ) e. ( J Cn J ) )
33	27, 27, 19	cnmptc 21465	. . . . . . . . . . . . . . 15 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( a e. ( Base ` G ) |-> x ) e. ( J Cn J ) )
34	1, 20, 25, 27, 32, 33	cnmpt1plusg 21891	. . . . . . . . . . . . . 14 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) e. ( J Cn J ) )
35		simprl 794	. . . . . . . . . . . . . 14 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> z e. J )
36		cnima 21069	. . . . . . . . . . . . . 14 |- ( ( ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) e. ( J Cn J ) /\ z e. J ) -> ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) e. J )
37	34, 35, 36	syl2anc 693	. . . . . . . . . . . . 13 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) e. J )
38		simplr 792	. . . . . . . . . . . . 13 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> A. w e. J ( x e. w -> y e. w ) )
39	13, 20, 15	grpnpcan 17507	. . . . . . . . . . . . . . . 16 |- ( ( G e. Grp /\ y e. ( Base ` G ) /\ x e. ( Base ` G ) ) -> ( ( y ( -g ` G ) x ) ( +g ` G ) x ) = y )
40	10, 12, 19, 39	syl3anc 1326	. . . . . . . . . . . . . . 15 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( ( y ( -g ` G ) x ) ( +g ` G ) x ) = y )
41		simprr 796	. . . . . . . . . . . . . . 15 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> y e. z )
42	40, 41	eqeltrd 2701	. . . . . . . . . . . . . 14 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( ( y ( -g ` G ) x ) ( +g ` G ) x ) e. z )
43		oveq2 6658	. . . . . . . . . . . . . . . . 17 |- ( a = x -> ( y ( -g ` G ) a ) = ( y ( -g ` G ) x ) )
44	43	oveq1d 6665	. . . . . . . . . . . . . . . 16 |- ( a = x -> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) = ( ( y ( -g ` G ) x ) ( +g ` G ) x ) )
45	44	eleq1d 2686	. . . . . . . . . . . . . . 15 |- ( a = x -> ( ( ( y ( -g ` G ) a ) ( +g ` G ) x ) e. z <-> ( ( y ( -g ` G ) x ) ( +g ` G ) x ) e. z ) )
46		eqid 2622	. . . . . . . . . . . . . . . 16 |- ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) = ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) )
47	46	mptpreima 5628	. . . . . . . . . . . . . . 15 |- ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) = { a e. ( Base ` G ) | ( ( y ( -g ` G ) a ) ( +g ` G ) x ) e. z }
48	45, 47	elrab2 3366	. . . . . . . . . . . . . 14 |- ( x e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) <-> ( x e. ( Base ` G ) /\ ( ( y ( -g ` G ) x ) ( +g ` G ) x ) e. z ) )
49	19, 42, 48	sylanbrc 698	. . . . . . . . . . . . 13 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> x e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) )
50		eleq2 2690	. . . . . . . . . . . . . . 15 |- ( w = ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) -> ( x e. w <-> x e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) ) )
51		eleq2 2690	. . . . . . . . . . . . . . 15 |- ( w = ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) -> ( y e. w <-> y e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) ) )
52	50, 51	imbi12d 334	. . . . . . . . . . . . . 14 |- ( w = ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) -> ( ( x e. w -> y e. w ) <-> ( x e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) -> y e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) ) ) )
53	52	rspcv 3305	. . . . . . . . . . . . 13 |- ( ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) e. J -> ( A. w e. J ( x e. w -> y e. w ) -> ( x e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) -> y e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) ) ) )
54	37, 38, 49, 53	syl3c 66	. . . . . . . . . . . 12 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> y e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) )
55		oveq2 6658	. . . . . . . . . . . . . . . 16 |- ( a = y -> ( y ( -g ` G ) a ) = ( y ( -g ` G ) y ) )
56	55	oveq1d 6665	. . . . . . . . . . . . . . 15 |- ( a = y -> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) = ( ( y ( -g ` G ) y ) ( +g ` G ) x ) )
57	56	eleq1d 2686	. . . . . . . . . . . . . 14 |- ( a = y -> ( ( ( y ( -g ` G ) a ) ( +g ` G ) x ) e. z <-> ( ( y ( -g ` G ) y ) ( +g ` G ) x ) e. z ) )
58	57, 47	elrab2 3366	. . . . . . . . . . . . 13 |- ( y e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) <-> ( y e. ( Base ` G ) /\ ( ( y ( -g ` G ) y ) ( +g ` G ) x ) e. z ) )
59	58	simprbi 480	. . . . . . . . . . . 12 |- ( y e. ( `' ( a e. ( Base ` G ) |-> ( ( y ( -g ` G ) a ) ( +g ` G ) x ) ) " z ) -> ( ( y ( -g ` G ) y ) ( +g ` G ) x ) e. z )
60	54, 59	syl 17	. . . . . . . . . . 11 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> ( ( y ( -g ` G ) y ) ( +g ` G ) x ) e. z )
61	23, 60	eqeltrrd 2702	. . . . . . . . . 10 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ ( z e. J /\ y e. z ) ) -> x e. z )
62	61	expr 643	. . . . . . . . 9 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ z e. J ) -> ( y e. z -> x e. z ) )
63	8, 62	impbid 202	. . . . . . . 8 |- ( ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) /\ z e. J ) -> ( x e. z <-> y e. z ) )
64	63	ralrimiva 2966	. . . . . . 7 |- ( ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) /\ A. w e. J ( x e. w -> y e. w ) ) -> A. z e. J ( x e. z <-> y e. z ) )
65	64	ex 450	. . . . . 6 |- ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) -> ( A. w e. J ( x e. w -> y e. w ) -> A. z e. J ( x e. z <-> y e. z ) ) )
66	65	imim1d 82	. . . . 5 |- ( ( G e. TopGrp /\ ( x e. ( Base ` G ) /\ y e. ( Base ` G ) ) ) -> ( ( A. z e. J ( x e. z <-> y e. z ) -> x = y ) -> ( A. w e. J ( x e. w -> y e. w ) -> x = y ) ) )
67	66	ralimdvva 2964	. . . 4 |- ( G e. TopGrp -> ( A. x e. ( Base ` G ) A. y e. ( Base ` G ) ( A. z e. J ( x e. z <-> y e. z ) -> x = y ) -> A. x e. ( Base ` G ) A. y e. ( Base ` G ) ( A. w e. J ( x e. w -> y e. w ) -> x = y ) ) )
68		ist0-2 21148	. . . . 5 |- ( J e. (TopOn ` ( Base ` G ) ) -> ( J e. Kol2 <-> A. x e. ( Base ` G ) A. y e. ( Base ` G ) ( A. z e. J ( x e. z <-> y e. z ) -> x = y ) ) )
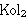
69	26, 68	syl 17	. . . 4 |- ( G e. TopGrp -> ( J e. Kol2 <-> A. x e. ( Base ` G ) A. y e. ( Base ` G ) ( A. z e. J ( x e. z <-> y e. z ) -> x = y ) ) )
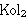
70		ist1-2 21151	. . . . 5 |- ( J e. (TopOn ` ( Base ` G ) ) -> ( J e. Fre <-> A. x e. ( Base ` G ) A. y e. ( Base ` G ) ( A. w e. J ( x e. w -> y e. w ) -> x = y ) ) )
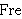
71	26, 70	syl 17	. . . 4 |- ( G e. TopGrp -> ( J e. Fre <-> A. x e. ( Base ` G ) A. y e. ( Base ` G ) ( A. w e. J ( x e. w -> y e. w ) -> x = y ) ) )
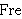
72	67, 69, 71	3imtr4d 283	. . 3 |- ( G e. TopGrp -> ( J e. Kol2 -> J e. Fre ) )
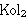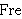73	3, 72	impbid2 216	. 2 |- ( G e. TopGrp -> ( J e. Fre <-> J e. Kol2 ) )
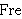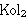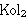74	2, 73	bitrd 268	1 |- ( G e. TopGrp -> ( J e. Haus <-> J e. Kol2 ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   e. wcel 1990   A.wral 2912   |-> cmpt 4729   `'ccnv 5113   "cima 5117   ` cfv 5888  (class class class)co 6650   Basecbs 15857   +g cplusg 15941   TopOpenctopn 16082   0gc0g 16100   Grpcgrp 17422   -gcsg 17424  TopOnctopon 20715   Cn ccn 21028   Kol2ct0 21110   Frect1 21111   Hauscha 21112   tX ctx 21363  TopMndctmd 21874   TopGrpctgp 21875

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-1st 7168  df-2nd 7169  df-map 7859  df-0g 16102  df-topgen 16104  df-plusf 17241  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-grp 17425  df-minusg 17426  df-sbg 17427  df-top 20699  df-topon 20716  df-topsp 20737  df-bases 20750  df-cld 20823  df-cn 21031  df-cnp 21032  df-t0 21117  df-t1 21118  df-haus 21119  df-tx 21365  df-tmd 21876  df-tgp 21877

This theorem is referenced by: (None)