Theorem trljco 36028

Description: Trace joined with trace of composition. (Contributed by NM, 15-Jun-2013.)

Hypotheses

Ref	Expression
trljco.j	|- .\/ = ( join ` K )
trljco.h	|- H = ( LHyp ` K )
trljco.t	|- T = ( ( LTrn ` K ) ` W )
trljco.r	|- R = ( ( trL ` K ) ` W )

Assertion

Ref	Expression
trljco	|- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` G ) ) )

Proof of Theorem trljco

Step	Hyp	Ref	Expression
1		coeq1 5279	. . . . 5 |- ( F = ( _I |` ( Base ` K ) ) -> ( F o. G ) = ( ( _I |` ( Base ` K ) ) o. G ) )
2		eqid 2622	. . . . . . . 8 |- ( Base ` K ) = ( Base ` K )
3		trljco.h	. . . . . . . 8 |- H = ( LHyp ` K )
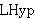4		trljco.t	. . . . . . . 8 |- T = ( ( LTrn ` K ) ` W )
5	2, 3, 4	ltrn1o 35410	. . . . . . 7 |- ( ( ( K e. HL /\ W e. H ) /\ G e. T ) -> G : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
6	5	3adant2 1080	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> G : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
7		f1of 6137	. . . . . 6 |- ( G : ( Base ` K ) -1-1-onto-> ( Base ` K ) -> G : ( Base ` K ) --> ( Base ` K ) )
8		fcoi2 6079	. . . . . 6 |- ( G : ( Base ` K ) --> ( Base ` K ) -> ( ( _I |` ( Base ` K ) ) o. G ) = G )
9	6, 7, 8	3syl 18	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( _I |` ( Base ` K ) ) o. G ) = G )
10	1, 9	sylan9eqr 2678	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ F = ( _I |` ( Base ` K ) ) ) -> ( F o. G ) = G )
11	10	fveq2d 6195	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ F = ( _I |` ( Base ` K ) ) ) -> ( R ` ( F o. G ) ) = ( R ` G ) )
12	11	oveq2d 6666	. 2 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ F = ( _I |` ( Base ` K ) ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` G ) ) )
13		simp1l 1085	. . . . . . 7 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> K e. HL )
14		hllat 34650	. . . . . . 7 |- ( K e. HL -> K e. Lat )
15	13, 14	syl 17	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> K e. Lat )
16		trljco.r	. . . . . . . 8 |- R = ( ( trL ` K ) ` W )
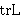17	2, 3, 4, 16	trlcl 35451	. . . . . . 7 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T ) -> ( R ` F ) e. ( Base ` K ) )
18	17	3adant3 1081	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( R ` F ) e. ( Base ` K ) )
19		trljco.j	. . . . . . 7 |- .\/ = ( join ` K )
20	2, 19	latjidm 17074	. . . . . 6 |- ( ( K e. Lat /\ ( R ` F ) e. ( Base ` K ) ) -> ( ( R ` F ) .\/ ( R ` F ) ) = ( R ` F ) )
21	15, 18, 20	syl2anc 693	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( R ` F ) ) = ( R ` F ) )
22		hlol 34648	. . . . . . 7 |- ( K e. HL -> K e. OL )
23	13, 22	syl 17	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> K e. OL )
24		eqid 2622	. . . . . . 7 |- ( 0. ` K ) = ( 0. ` K )
25	2, 19, 24	olj01 34512	. . . . . 6 |- ( ( K e. OL /\ ( R ` F ) e. ( Base ` K ) ) -> ( ( R ` F ) .\/ ( 0. ` K ) ) = ( R ` F ) )
26	23, 18, 25	syl2anc 693	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( 0. ` K ) ) = ( R ` F ) )
27	21, 26	eqtr4d 2659	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( R ` F ) ) = ( ( R ` F ) .\/ ( 0. ` K ) ) )
28	27	adantr 481	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ G = ( _I |` ( Base ` K ) ) ) -> ( ( R ` F ) .\/ ( R ` F ) ) = ( ( R ` F ) .\/ ( 0. ` K ) ) )
29		coeq2 5280	. . . . . 6 |- ( G = ( _I |` ( Base ` K ) ) -> ( F o. G ) = ( F o. ( _I |` ( Base ` K ) ) ) )
30	2, 3, 4	ltrn1o 35410	. . . . . . . 8 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T ) -> F : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
31	30	3adant3 1081	. . . . . . 7 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> F : ( Base ` K ) -1-1-onto-> ( Base ` K ) )
32		f1of 6137	. . . . . . 7 |- ( F : ( Base ` K ) -1-1-onto-> ( Base ` K ) -> F : ( Base ` K ) --> ( Base ` K ) )
33		fcoi1 6078	. . . . . . 7 |- ( F : ( Base ` K ) --> ( Base ` K ) -> ( F o. ( _I |` ( Base ` K ) ) ) = F )
34	31, 32, 33	3syl 18	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( F o. ( _I |` ( Base ` K ) ) ) = F )
35	29, 34	sylan9eqr 2678	. . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ G = ( _I |` ( Base ` K ) ) ) -> ( F o. G ) = F )
36	35	fveq2d 6195	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ G = ( _I |` ( Base ` K ) ) ) -> ( R ` ( F o. G ) ) = ( R ` F ) )
37	36	oveq2d 6666	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ G = ( _I |` ( Base ` K ) ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` F ) ) )
38	2, 24, 3, 4, 16	trlid0b 35465	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ G e. T ) -> ( G = ( _I |` ( Base ` K ) ) <-> ( R ` G ) = ( 0. ` K ) ) )
39	38	3adant2 1080	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( G = ( _I |` ( Base ` K ) ) <-> ( R ` G ) = ( 0. ` K ) ) )
40	39	biimpa 501	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ G = ( _I |` ( Base ` K ) ) ) -> ( R ` G ) = ( 0. ` K ) )
41	40	oveq2d 6666	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ G = ( _I |` ( Base ` K ) ) ) -> ( ( R ` F ) .\/ ( R ` G ) ) = ( ( R ` F ) .\/ ( 0. ` K ) ) )
42	28, 37, 41	3eqtr4d 2666	. 2 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ G = ( _I |` ( Base ` K ) ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` G ) ) )
43		eqid 2622	. . 3 |- ( le ` K ) = ( le ` K )
44	15	adantr 481	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> K e. Lat )
45		simp1 1061	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( K e. HL /\ W e. H ) )
46	3, 4	ltrnco 36007	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( F o. G ) e. T )
47	2, 3, 4, 16	trlcl 35451	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ ( F o. G ) e. T ) -> ( R ` ( F o. G ) ) e. ( Base ` K ) )
48	45, 46, 47	syl2anc 693	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( R ` ( F o. G ) ) e. ( Base ` K ) )
49	2, 19	latjcl 17051	. . . . 5 |- ( ( K e. Lat /\ ( R ` F ) e. ( Base ` K ) /\ ( R ` ( F o. G ) ) e. ( Base ` K ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) e. ( Base ` K ) )
50	15, 18, 48, 49	syl3anc 1326	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) e. ( Base ` K ) )
51	50	adantr 481	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) e. ( Base ` K ) )
52	2, 3, 4, 16	trlcl 35451	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ G e. T ) -> ( R ` G ) e. ( Base ` K ) )
53	52	3adant2 1080	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( R ` G ) e. ( Base ` K ) )
54	2, 19	latjcl 17051	. . . . 5 |- ( ( K e. Lat /\ ( R ` F ) e. ( Base ` K ) /\ ( R ` G ) e. ( Base ` K ) ) -> ( ( R ` F ) .\/ ( R ` G ) ) e. ( Base ` K ) )
55	15, 18, 53, 54	syl3anc 1326	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( R ` G ) ) e. ( Base ` K ) )
56	55	adantr 481	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> ( ( R ` F ) .\/ ( R ` G ) ) e. ( Base ` K ) )
57	2, 43, 19	latlej1 17060	. . . . . 6 |- ( ( K e. Lat /\ ( R ` F ) e. ( Base ` K ) /\ ( R ` G ) e. ( Base ` K ) ) -> ( R ` F ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) )
58	15, 18, 53, 57	syl3anc 1326	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( R ` F ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) )
59	43, 19, 3, 4, 16	trlco 36015	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( R ` ( F o. G ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) )
60	2, 43, 19	latjle12 17062	. . . . . 6 |- ( ( K e. Lat /\ ( ( R ` F ) e. ( Base ` K ) /\ ( R ` ( F o. G ) ) e. ( Base ` K ) /\ ( ( R ` F ) .\/ ( R ` G ) ) e. ( Base ` K ) ) ) -> ( ( ( R ` F ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) /\ ( R ` ( F o. G ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) ) <-> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) ) )
61	15, 18, 48, 55, 60	syl13anc 1328	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( ( R ` F ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) /\ ( R ` ( F o. G ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) ) <-> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) ) )
62	58, 59, 61	mpbi2and 956	. . . 4 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) )
63	62	adantr 481	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) )
64		simpr 477	. . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> ( R ` F ) = ( R ` G ) )
65	64	oveq2d 6666	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> ( ( R ` F ) .\/ ( R ` F ) ) = ( ( R ` F ) .\/ ( R ` G ) ) )
66	2, 43, 19	latlej1 17060	. . . . . . 7 |- ( ( K e. Lat /\ ( R ` F ) e. ( Base ` K ) /\ ( R ` ( F o. G ) ) e. ( Base ` K ) ) -> ( R ` F ) ( le ` K ) ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) )
67	15, 18, 48, 66	syl3anc 1326	. . . . . 6 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( R ` F ) ( le ` K ) ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) )
68	21, 67	eqbrtrd 4675	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( R ` F ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) )
69	68	adantr 481	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> ( ( R ` F ) .\/ ( R ` F ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) )
70	65, 69	eqbrtrrd 4677	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> ( ( R ` F ) .\/ ( R ` G ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) )
71	2, 43, 44, 51, 56, 63, 70	latasymd 17057	. 2 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( R ` F ) = ( R ` G ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` G ) ) )
72	62	adantr 481	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) )
73		simpl1l 1112	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> K e. HL )
74		simpl1 1064	. . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( K e. HL /\ W e. H ) )
75		simpl2 1065	. . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> F e. T )
76		simpr1 1067	. . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> F =/= ( _I |` ( Base ` K ) ) )
77		eqid 2622	. . . . . 6 |- ( Atoms ` K ) = ( Atoms ` K )
78	2, 77, 3, 4, 16	trlnidat 35460	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ F =/= ( _I |` ( Base ` K ) ) ) -> ( R ` F ) e. ( Atoms ` K ) )
79	74, 75, 76, 78	syl3anc 1326	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( R ` F ) e. ( Atoms ` K ) )
80		simpl3 1066	. . . . . 6 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> G e. T )
81	75, 80	jca 554	. . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( F e. T /\ G e. T ) )
82		simpr3 1069	. . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( R ` F ) =/= ( R ` G ) )
83	77, 3, 4, 16	trlcoat 36011	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ ( F e. T /\ G e. T ) /\ ( R ` F ) =/= ( R ` G ) ) -> ( R ` ( F o. G ) ) e. ( Atoms ` K ) )
84	74, 81, 82, 83	syl3anc 1326	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( R ` ( F o. G ) ) e. ( Atoms ` K ) )
85		simpr2 1068	. . . . 5 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> G =/= ( _I |` ( Base ` K ) ) )
86	2, 3, 4, 16	trlcone 36016	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ ( F e. T /\ G e. T ) /\ ( ( R ` F ) =/= ( R ` G ) /\ G =/= ( _I |` ( Base ` K ) ) ) ) -> ( R ` F ) =/= ( R ` ( F o. G ) ) )
87	74, 81, 82, 85, 86	syl112anc 1330	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( R ` F ) =/= ( R ` ( F o. G ) ) )
88	2, 77, 3, 4, 16	trlnidat 35460	. . . . 5 |- ( ( ( K e. HL /\ W e. H ) /\ G e. T /\ G =/= ( _I |` ( Base ` K ) ) ) -> ( R ` G ) e. ( Atoms ` K ) )
89	74, 80, 85, 88	syl3anc 1326	. . . 4 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( R ` G ) e. ( Atoms ` K ) )
90	43, 19, 77	ps-1 34763	. . . 4 |- ( ( K e. HL /\ ( ( R ` F ) e. ( Atoms ` K ) /\ ( R ` ( F o. G ) ) e. ( Atoms ` K ) /\ ( R ` F ) =/= ( R ` ( F o. G ) ) ) /\ ( ( R ` F ) e. ( Atoms ` K ) /\ ( R ` G ) e. ( Atoms ` K ) ) ) -> ( ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) <-> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` G ) ) ) )
91	73, 79, 84, 87, 79, 89, 90	syl132anc 1344	. . 3 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) ( le ` K ) ( ( R ` F ) .\/ ( R ` G ) ) <-> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` G ) ) ) )
92	72, 91	mpbid 222	. 2 |- ( ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) /\ ( F =/= ( _I |` ( Base ` K ) ) /\ G =/= ( _I |` ( Base ` K ) ) /\ ( R ` F ) =/= ( R ` G ) ) ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` G ) ) )
93	12, 42, 71, 92	pm2.61da3ne 2883	1 |- ( ( ( K e. HL /\ W e. H ) /\ F e. T /\ G e. T ) -> ( ( R ` F ) .\/ ( R ` ( F o. G ) ) ) = ( ( R ` F ) .\/ ( R ` G ) ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   class class class wbr 4653   _I cid 5023   |` cres 5116   o. ccom 5118   -->wf 5884   -1-1-onto->wf1o 5887   ` cfv 5888  (class class class)co 6650   Basecbs 15857   lecple 15948   joincjn 16944   0.cp0 17037   Latclat 17045   OLcol 34461   Atomscatm 34550   HLchlt 34637   LHypclh 35270   LTrncltrn 35387   trLctrl 35445

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-riotaBAD 34239

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-op 4184  df-uni 4437  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-id 5024  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-1st 7168  df-2nd 7169  df-undef 7399  df-map 7859  df-preset 16928  df-poset 16946  df-plt 16958  df-lub 16974  df-glb 16975  df-join 16976  df-meet 16977  df-p0 17039  df-p1 17040  df-lat 17046  df-clat 17108  df-oposet 34463  df-ol 34465  df-oml 34466  df-covers 34553  df-ats 34554  df-atl 34585  df-cvlat 34609  df-hlat 34638  df-llines 34784  df-lplanes 34785  df-lvols 34786  df-lines 34787  df-psubsp 34789  df-pmap 34790  df-padd 35082  df-lhyp 35274  df-laut 35275  df-ldil 35390  df-ltrn 35391  df-trl 35446

This theorem is referenced by:  trljco2  36029  cdlemkid1  36210