Description: A ZFC emulation of
Hilbert's transfinite axiom. The set  has the
properties of Hilbert's epsilon, except that it also depends on a
well-ordering has the
properties of Hilbert's epsilon, except that it also depends on a
well-ordering  .
This theorem arose from discussions with Raph
Levien on 5-Mar-2004 about translating the HOL proof language, which
uses Hilbert's epsilon. See
http://us.metamath.org/downloads/choice.txt
(copy of obsolete link
http://ghilbert.org/choice.txt) and
http://us.metamath.org/downloads/megillaward2005he.pdf. .
This theorem arose from discussions with Raph
Levien on 5-Mar-2004 about translating the HOL proof language, which
uses Hilbert's epsilon. See
http://us.metamath.org/downloads/choice.txt
(copy of obsolete link
http://ghilbert.org/choice.txt) and
http://us.metamath.org/downloads/megillaward2005he.pdf.
Hilbert's epsilon is described at
http://plato.stanford.edu/entries/epsilon-calculus/.
This theorem
differs from Hilbert's transfinite axiom described on that page in that
it requires 
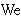  as an antecedent. Class as an antecedent. Class  collects the sets
of the least rank for which collects the sets
of the least rank for which     is true. Class is true. Class  , which
emulates the epsilon, is the minimum element in a well-ordering , which
emulates the epsilon, is the minimum element in a well-ordering  on on
 . .
If a well-ordering  on on  can be
expressed in a closed form, as
might be the case if we are working with say natural numbers, we can
eliminate the antecedent with modus ponens, giving us the exact
equivalent of Hilbert's transfinite axiom. Otherwise, we replace can be
expressed in a closed form, as
might be the case if we are working with say natural numbers, we can
eliminate the antecedent with modus ponens, giving us the exact
equivalent of Hilbert's transfinite axiom. Otherwise, we replace  with a dummy setvar variable, say
with a dummy setvar variable, say  , and attach , and attach  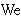  as an
antecedent in each step of the ZFC version of the HOL proof until the
epsilon is eliminated. At that point, as an
antecedent in each step of the ZFC version of the HOL proof until the
epsilon is eliminated. At that point,  (which will have (which will have  as a
free variable) will no longer be present, and we can eliminate as a
free variable) will no longer be present, and we can eliminate
 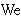  by applying exlimiv 1858 and weth 9317, using scottexs 8750 to
establish the existence of by applying exlimiv 1858 and weth 9317, using scottexs 8750 to
establish the existence of  . .
For a version of this theorem scheme using class (meta)variables instead
of wff (meta)variables, see htalem 8759. (Contributed by NM,
11-Mar-2004.) (Revised by Mario Carneiro,
25-Jun-2015.) |