lnophmlem2 - Hilbert Space Explorer

	Hilbert Space Explorer		< Previous Next > Nearby theorems
Mirrors > Home > HSE Home > Th. List > lnophmlem2		Structured version Visualization version Unicode version

Theorem lnophmlem2 28876

Description: Lemma for lnophmi 28877. (Contributed by NM, 24-Jan-2006.) (New usage is discouraged.)

**Hypotheses**
Ref	Expression
lnophmlem.1
lnophmlem.2
lnophmlem.3
lnophmlem.4

**Assertion**
Ref	Expression
lnophmlem2

Distinct variable groups:

**Proof of Theorem lnophmlem2**
Step	Hyp	Ref	Expression
1		lnophmlem.2	. . . . . 6
2		lnophmlem.1	. . . . . . 7
3		lnophmlem.3	. . . . . . . . 9
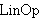4	3	lnopfi 28828	. . . . . . . 8
5	4	ffvelrni 6358	. . . . . . 7
6	2, 5	ax-mp 5	. . . . . 6
7	4	ffvelrni 6358	. . . . . . 7
8	1, 7	ax-mp 5	. . . . . 6
9	1, 6, 2, 8	polid2i 28014	. . . . 5
10	1, 2	hvcomi 27876	. . . . . . . . 9
11	8, 6	hvcomi 27876	. . . . . . . . . 10
12	3	lnopaddi 28830	. . . . . . . . . . 11 $/\$
13	2, 1, 12	mp2an 708	. . . . . . . . . 10
14	11, 13	eqtr4i 2647	. . . . . . . . 9
15	10, 14	oveq12i 6662	. . . . . . . 8
16	1, 2, 8, 6	hisubcomi 27961	. . . . . . . . 9
17	3	lnopsubi 28833	. . . . . . . . . . 11 $/\$
18	2, 1, 17	mp2an 708	. . . . . . . . . 10
19	18	oveq2i 6661	. . . . . . . . 9
20	16, 19	eqtr4i 2647	. . . . . . . 8
21	15, 20	oveq12i 6662	. . . . . . 7
22		ax-icn 9995	. . . . . . . . . . 11
23	22, 1	hvmulcli 27871	. . . . . . . . . . . 12
24	2, 23	hvsubcli 27878	. . . . . . . . . . 11
25	4	ffvelrni 6358	. . . . . . . . . . . 12
26	24, 25	ax-mp 5	. . . . . . . . . . 11
27	22, 22, 24, 26	his35i 27946	. . . . . . . . . 10
28	22, 2, 23	hvsubdistr1i 27909	. . . . . . . . . . . 12
29	22, 2	hvmulcli 27871	. . . . . . . . . . . . . 14
30	22, 23	hvmulcli 27871	. . . . . . . . . . . . . 14
31	29, 30	hvsubvali 27877	. . . . . . . . . . . . 13
32	22, 22, 1	hvmulassi 27903	. . . . . . . . . . . . . . . 16
33	32	oveq2i 6661	. . . . . . . . . . . . . . 15
34		ixi 10656	. . . . . . . . . . . . . . . . . . 19
35	34	oveq2i 6661	. . . . . . . . . . . . . . . . . 18
36		ax-1cn 9994	. . . . . . . . . . . . . . . . . . 19
37	36, 36	mul2negi 10478	. . . . . . . . . . . . . . . . . 18
38		1t1e1 11175	. . . . . . . . . . . . . . . . . 18
39	35, 37, 38	3eqtri 2648	. . . . . . . . . . . . . . . . 17
40	39	oveq1i 6660	. . . . . . . . . . . . . . . 16
41		neg1cn 11124	. . . . . . . . . . . . . . . . 17
42	22, 22	mulcli 10045	. . . . . . . . . . . . . . . . 17
43	41, 42, 1	hvmulassi 27903	. . . . . . . . . . . . . . . 16
44		ax-hvmulid 27863	. . . . . . . . . . . . . . . . 17
45	1, 44	ax-mp 5	. . . . . . . . . . . . . . . 16
46	40, 43, 45	3eqtr3i 2652	. . . . . . . . . . . . . . 15
47	33, 46	eqtr3i 2646	. . . . . . . . . . . . . 14
48	47	oveq2i 6661	. . . . . . . . . . . . 13
49	31, 48	eqtri 2644	. . . . . . . . . . . 12
50	29, 1	hvcomi 27876	. . . . . . . . . . . 12
51	28, 49, 50	3eqtri 2648	. . . . . . . . . . 11
52	51	fveq2i 6194	. . . . . . . . . . . 12
53	3	lnopmuli 28831	. . . . . . . . . . . . 13 $/\$
54	22, 24, 53	mp2an 708	. . . . . . . . . . . 12
55	3	lnopaddmuli 28832	. . . . . . . . . . . . 13 $/\$ $/\$
56	22, 1, 2, 55	mp3an 1424	. . . . . . . . . . . 12
57	52, 54, 56	3eqtr3i 2652	. . . . . . . . . . 11
58	51, 57	oveq12i 6662	. . . . . . . . . 10
59		cji 13899	. . . . . . . . . . . . . 14
60	59	oveq2i 6661	. . . . . . . . . . . . 13
61	22, 22	mulneg2i 10477	. . . . . . . . . . . . 13
62	34	negeqi 10274	. . . . . . . . . . . . . 14
63		negneg1e1 11128	. . . . . . . . . . . . . 14
64	62, 63	eqtri 2644	. . . . . . . . . . . . 13
65	60, 61, 64	3eqtri 2648	. . . . . . . . . . . 12
66	65	oveq1i 6660	. . . . . . . . . . 11
67		lnophmlem.4	. . . . . . . . . . . . . 14
68	24, 2, 3, 67	lnophmlem1 28875	. . . . . . . . . . . . 13
69	68	recni 10052	. . . . . . . . . . . 12
70	69	mulid2i 10043	. . . . . . . . . . 11
71	66, 70	eqtri 2644	. . . . . . . . . 10
72	27, 58, 71	3eqtr3i 2652	. . . . . . . . 9
73	22, 6	hvmulcli 27871	. . . . . . . . . . . 12
74	1, 29, 8, 73	hisubcomi 27961	. . . . . . . . . . 11
75	34	oveq1i 6660	. . . . . . . . . . . . . . 15
76	32, 75	eqtr3i 2646	. . . . . . . . . . . . . 14
77	76	oveq2i 6661	. . . . . . . . . . . . 13
78	22, 2, 23	hvdistr1i 27908	. . . . . . . . . . . . 13
79	29, 1	hvsubvali 27877	. . . . . . . . . . . . 13
80	77, 78, 79	3eqtr4i 2654	. . . . . . . . . . . 12
81	80	fveq2i 6194	. . . . . . . . . . . . 13
82	2, 23	hvaddcli 27875	. . . . . . . . . . . . . 14
83	3	lnopmuli 28831	. . . . . . . . . . . . . 14 $/\$
84	22, 82, 83	mp2an 708	. . . . . . . . . . . . 13
85	3	lnopmulsubi 28835	. . . . . . . . . . . . . 14 $/\$ $/\$
86	22, 2, 1, 85	mp3an 1424	. . . . . . . . . . . . 13
87	81, 84, 86	3eqtr3i 2652	. . . . . . . . . . . 12
88	80, 87	oveq12i 6662	. . . . . . . . . . 11
89	74, 88	eqtr4i 2647	. . . . . . . . . 10
90	4	ffvelrni 6358	. . . . . . . . . . . 12
91	82, 90	ax-mp 5	. . . . . . . . . . 11
92	22, 22, 82, 91	his35i 27946	. . . . . . . . . 10
93	65	oveq1i 6660	. . . . . . . . . . 11
94	82, 2, 3, 67	lnophmlem1 28875	. . . . . . . . . . . . 13
95	94	recni 10052	. . . . . . . . . . . 12
96	95	mulid2i 10043	. . . . . . . . . . 11
97	93, 96	eqtri 2644	. . . . . . . . . 10
98	89, 92, 97	3eqtri 2648	. . . . . . . . 9
99	72, 98	oveq12i 6662	. . . . . . . 8
100	99	oveq2i 6661	. . . . . . 7
101	21, 100	oveq12i 6662	. . . . . 6
102	101	oveq1i 6660	. . . . 5
103	9, 102	eqtri 2644	. . . 4
104	103	fveq2i 6194	. . 3
105		4ne0 11117	. . . 4
106	2, 1	hvaddcli 27875	. . . . . . . . 9
107	106, 2, 3, 67	lnophmlem1 28875	. . . . . . . 8
108	2, 1	hvsubcli 27878	. . . . . . . . 9
109	108, 2, 3, 67	lnophmlem1 28875	. . . . . . . 8
110	107, 109	resubcli 10343	. . . . . . 7
111	110	recni 10052	. . . . . 6
112	68, 94	resubcli 10343	. . . . . . . 8
113	112	recni 10052	. . . . . . 7
114	22, 113	mulcli 10045	. . . . . 6
115	111, 114	addcli 10044	. . . . 5
116		4re 11097	. . . . . 6
117	116	recni 10052	. . . . 5
118	115, 117	cjdivi 13931	. . . 4
119	105, 118	ax-mp 5	. . 3
120		cjreim 13900	. . . . . . 7 $/\$
121	110, 112, 120	mp2an 708	. . . . . 6
122	82, 1, 3, 67	lnophmlem1 28875	. . . . . . . . . 10
123	68, 122	resubcli 10343	. . . . . . . . 9
124	123	recni 10052	. . . . . . . 8
125	22, 124	mulcli 10045	. . . . . . 7
126	111, 125	negsubi 10359	. . . . . 6
127	121, 126	eqtr4i 2647	. . . . 5
128	22, 113	mulneg2i 10477	. . . . . . 7
129	69, 95	negsubdi2i 10367	. . . . . . . 8
130	129	oveq2i 6661	. . . . . . 7
131	128, 130	eqtr3i 2646	. . . . . 6
132	131	oveq2i 6661	. . . . 5
133	13	oveq2i 6661	. . . . . . 7
134	133, 19	oveq12i 6662	. . . . . 6
135	3	lnopaddmuli 28832	. . . . . . . . . 10 $/\$ $/\$
136	22, 2, 1, 135	mp3an 1424	. . . . . . . . 9
137	136	oveq2i 6661	. . . . . . . 8
138	3	lnopsubmuli 28834	. . . . . . . . . 10 $/\$ $/\$
139	22, 2, 1, 138	mp3an 1424	. . . . . . . . 9
140	139	oveq2i 6661	. . . . . . . 8
141	137, 140	oveq12i 6662	. . . . . . 7
142	141	oveq2i 6661	. . . . . 6
143	134, 142	oveq12i 6662	. . . . 5
144	127, 132, 143	3eqtri 2648	. . . 4
145		cjre 13879	. . . . 5
146	116, 145	ax-mp 5	. . . 4
147	144, 146	oveq12i 6662	. . 3
148	104, 119, 147	3eqtrri 2649	. 2
149	2, 8, 1, 6	polid2i 28014	. 2
150	6, 1	his1i 27957	. 2
151	148, 149, 150	3eqtr4i 2654	1

Colors of variables: wff setvar class

Syntax hints:

wceq 1483

wcel 1990

wne 2794

wral 2912

cfv 5888 (class class class)co 6650

cc 9934

cr 9935

cc0 9936

c1 9937

ci 9938

caddc 9939

cmul 9941

cmin 10266

cneg 10267

cdiv 10684

c4 11072

ccj 13836

chil 27776

cva 27777

csm 27778

csp 27779

cmv 27782

clo 27804

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949 ax-resscn 9993 ax-1cn 9994 ax-icn 9995 ax-addcl 9996 ax-addrcl 9997 ax-mulcl 9998 ax-mulrcl 9999 ax-mulcom 10000 ax-addass 10001 ax-mulass 10002 ax-distr 10003 ax-i2m1 10004 ax-1ne0 10005 ax-1rid 10006 ax-rnegex 10007 ax-rrecex 10008 ax-cnre 10009 ax-pre-lttri 10010 ax-pre-lttrn 10011 ax-pre-ltadd 10012 ax-pre-mulgt0 10013 ax-hilex 27856 ax-hfvadd 27857 ax-hvcom 27858 ax-hvass 27859 ax-hv0cl 27860 ax-hvaddid 27861 ax-hfvmul 27862 ax-hvmulid 27863 ax-hvmulass 27864 ax-hvdistr1 27865 ax-hvdistr2 27866 ax-hvmul0 27867 ax-hfi 27936 ax-his1 27939 ax-his2 27940 ax-his3 27941

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3or 1038 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-nel 2898 df-ral 2917 df-rex 2918 df-reu 2919 df-rmo 2920 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-op 4184 df-uni 4437 df-iun 4522 df-br 4654 df-opab 4713 df-mpt 4730 df-id 5024 df-po 5035 df-so 5036 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-mpt2 6655 df-er 7742 df-map 7859 df-en 7956 df-dom 7957 df-sdom 7958 df-pnf 10076 df-mnf 10077 df-xr 10078 df-ltxr 10079 df-le 10080 df-sub 10268 df-neg 10269 df-div 10685 df-2 11079 df-3 11080 df-4 11081 df-cj 13839 df-re 13840 df-im 13841 df-hvsub 27828 df-lnop 28700

This theorem is referenced by: lnophmi 28877

W3C validator