| Step | Hyp | Ref
| Expression |
|---|
| 1 | | ltrelsr 9889 |
. . . . 5
    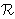  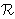  |
| 2 | 1 | brel 5168 |
. . . 4
    
    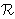    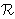   |
| 3 | 2 | simprd 479 |
. . 3
    
   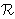  |
| 4 | 1 | brel 5168 |
. . . 4
    
    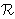    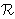   |
| 5 | 4 | simprd 479 |
. . 3
    
   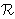  |
| 6 | 3, 5 | anim12i 590 |
. 2
    
          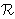    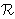   |
| 7 | | df-nr 9878 |
. . 3
 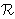           |
| 8 | | breq2 4657 |
. . . . 5
        ![] ]](rbrack.gif)              ![] ]](rbrack.gif)        |
| 9 | 8 | anbi1d 741 |
. . . 4
        ![] ]](rbrack.gif)               ![] ]](rbrack.gif)           ![] ]](rbrack.gif)   
             ![] ]](rbrack.gif)     |
| 10 | | oveq1 6657 |
. . . . 5
        ![] ]](rbrack.gif)            ![] ]](rbrack.gif)  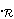       ![] ]](rbrack.gif)      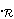       ![] ]](rbrack.gif)    |
| 11 | 10 | breq2d 4665 |
. . . 4
        ![] ]](rbrack.gif)               ![] ]](rbrack.gif)  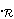       ![] ]](rbrack.gif)   
    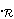       ![] ]](rbrack.gif)     |
| 12 | 9, 11 | imbi12d 334 |
. . 3
        ![] ]](rbrack.gif)                ![] ]](rbrack.gif)           ![] ]](rbrack.gif)             ![] ]](rbrack.gif)  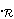       ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)        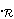       ![] ]](rbrack.gif)      |
| 13 | | breq2 4657 |
. . . . 5
        ![] ]](rbrack.gif)              ![] ]](rbrack.gif)        |
| 14 | 13 | anbi2d 740 |
. . . 4
        ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)               |
| 15 | | oveq2 6658 |
. . . . 5
        ![] ]](rbrack.gif)       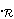       ![] ]](rbrack.gif)      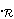    |
| 16 | 15 | breq2d 4665 |
. . . 4
        ![] ]](rbrack.gif)          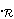       ![] ]](rbrack.gif)        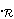     |
| 17 | 14, 16 | imbi12d 334 |
. . 3
        ![] ]](rbrack.gif)          
         ![] ]](rbrack.gif)        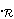       ![] ]](rbrack.gif)    
               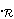      |
| 18 | | gt0srpr 9899 |
. . . . 5
          ![] ]](rbrack.gif)  
    |
| 19 | | gt0srpr 9899 |
. . . . 5
          ![] ]](rbrack.gif)  
    |
| 20 | 18, 19 | anbi12i 733 |
. . . 4
    
      ![] ]](rbrack.gif)    
      ![] ]](rbrack.gif)      
       |
| 21 | | simprr 796 |
. . . . . 6
                       
    |
| 22 | | mulclpr 9842 |
. . . . . . . 8
        
           |
| 23 | | mulclpr 9842 |
. . . . . . . 8
        
           |
| 24 | | addclpr 9840 |
. . . . . . . 8
                             
      |
| 25 | 22, 23, 24 | syl2an 494 |
. . . . . . 7
                       
   
            |
| 26 | 25 | an4s 869 |
. . . . . 6
                       
   
            |
| 27 | | ltexpri 9865 |
. . . . . . . . 9
    
             |
| 28 | | ltexpri 9865 |
. . . . . . . . 9
    
             |
| 29 | | mulclpr 9842 |
. . . . . . . . . . . . . . . . 17
        
           |
| 30 | | oveq12 6659 |
. . . . . . . . . . . . . . . . . . . . . 22
            
                
          |
| 31 | 30 | oveq1d 6665 |
. . . . . . . . . . . . . . . . . . . . 21
            
                            
                        
     |
| 32 | | distrpr 9850 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
                    
   |
| 33 | | oveq2 6658 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
            
             |
| 34 | 32, 33 | syl5eqr 2670 |
. . . . . . . . . . . . . . . . . . . . . . . 24
                
             |
| 35 | 34 | oveq1d 6665 |
. . . . . . . . . . . . . . . . . . . . . . 23
                    
   
   
                        
        |
| 36 | | vex 3203 |
. . . . . . . . . . . . . . . . . . . . . . . . . 26
    |
| 37 | | vex 3203 |
. . . . . . . . . . . . . . . . . . . . . . . . . 26
    |
| 38 | | vex 3203 |
. . . . . . . . . . . . . . . . . . . . . . . . . 26
    |
| 39 | | mulcompr 9845 |
. . . . . . . . . . . . . . . . . . . . . . . . . 26
            |
| 40 | | distrpr 9850 |
. . . . . . . . . . . . . . . . . . . . . . . . . 26
                    
   |
| 41 | 36, 37, 38, 39, 40 | caovdir 6868 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
                    
   |
| 42 | | vex 3203 |
. . . . . . . . . . . . . . . . . . . . . . . . . 26
    |
| 43 | 36, 37, 42, 39, 40 | caovdir 6868 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
                    
   |
| 44 | 41, 43 | oveq12i 6662 |
. . . . . . . . . . . . . . . . . . . . . . . 24
        
                        
   
   
          |
| 45 | | distrpr 9850 |
. . . . . . . . . . . . . . . . . . . . . . . 24
                                
   |
| 46 | | ovex 6678 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
        |
| 47 | | ovex 6678 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
        |
| 48 | | ovex 6678 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
        |
| 49 | | addcompr 9843 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
            |
| 50 | | addasspr 9844 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
                
   |
| 51 | | ovex 6678 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
        |
| 52 | 46, 47, 48, 49, 50, 51 | caov4 6865 |
. . . . . . . . . . . . . . . . . . . . . . . 24
        
                
               
   
   
          |
| 53 | 44, 45, 52 | 3eqtr4i 2654 |
. . . . . . . . . . . . . . . . . . . . . . 23
                                    
       |
| 54 | | ovex 6678 |
. . . . . . . . . . . . . . . . . . . . . . . 24
        |
| 55 | 48, 54, 51, 49, 50 | caov12 6862 |
. . . . . . . . . . . . . . . . . . . . . . 23
                                    
       |
| 56 | 35, 53, 55 | 3eqtr4g 2681 |
. . . . . . . . . . . . . . . . . . . . . 22
                
                    
        |
| 57 | | oveq1 6657 |
. . . . . . . . . . . . . . . . . . . . . . 23
                
         |
| 58 | 41, 57 | syl5eqr 2670 |
. . . . . . . . . . . . . . . . . . . . . 22
                
             |
| 59 | 56, 58 | oveqan12rd 6670 |
. . . . . . . . . . . . . . . . . . . . 21
            
                            
                                      |
| 60 | 31, 59 | eqtr3d 2658 |
. . . . . . . . . . . . . . . . . . . 20
            
                    
                                      |
| 61 | | addasspr 9844 |
. . . . . . . . . . . . . . . . . . . . 21
        
                    
   
          |
| 62 | | addcompr 9843 |
. . . . . . . . . . . . . . . . . . . . 21
        
                    
   
          |
| 63 | 61, 62 | eqtr3i 2646 |
. . . . . . . . . . . . . . . . . . . 20
                                    
       |
| 64 | | addasspr 9844 |
. . . . . . . . . . . . . . . . . . . . 21
        
                
           
   
            
     |
| 65 | | ovex 6678 |
. . . . . . . . . . . . . . . . . . . . . 22
                |
| 66 | | ovex 6678 |
. . . . . . . . . . . . . . . . . . . . . 22
        |
| 67 | 48, 65, 66, 49, 50 | caov32 6861 |
. . . . . . . . . . . . . . . . . . . . 21
        
   
                            
   
   
          |
| 68 | | addasspr 9844 |
. . . . . . . . . . . . . . . . . . . . . 22
        
                    
   
          |
| 69 | 68 | oveq2i 6661 |
. . . . . . . . . . . . . . . . . . . . 21
                                            
   
           |
| 70 | 64, 67, 69 | 3eqtr4i 2654 |
. . . . . . . . . . . . . . . . . . . 20
        
   
                        
       
              |
| 71 | 60, 63, 70 | 3eqtr3g 2679 |
. . . . . . . . . . . . . . . . . . 19
            
                    
                                
     |
| 72 | | addcanpr 9868 |
. . . . . . . . . . . . . . . . . . 19
                    
                        
           
       
                        
           
               |
| 73 | 71, 72 | syl5 34 |
. . . . . . . . . . . . . . . . . 18
                    
                                
                        
     |
| 74 | | eqcom 2629 |
. . . . . . . . . . . . . . . . . . . 20
        
                        
                                
       |
| 75 | | ltaddpr2 9857 |
. . . . . . . . . . . . . . . . . . . 20
        
                 
                    
                
                   |
| 76 | 74, 75 | syl5bi 232 |
. . . . . . . . . . . . . . . . . . 19
        
                                         
   
   
                
        |
| 77 | 76 | adantl 482 |
. . . . . . . . . . . . . . . . . 18
                    
                                
   
                
                   |
| 78 | 73, 77 | syld 47 |
. . . . . . . . . . . . . . . . 17
                    
                                
                
     |
| 79 | 29, 78 | sylan 488 |
. . . . . . . . . . . . . . . 16
                      
                                
                
     |
| 80 | 79 | a1d 25 |
. . . . . . . . . . . . . . 15
                      
                                     
                
      |
| 81 | 80 | exp4a 633 |
. . . . . . . . . . . . . 14
                      
                             
   
                
          |
| 82 | 81 | com34 91 |
. . . . . . . . . . . . 13
                      
                             
   
                
          |
| 83 | 82 | rexlimdv 3030 |
. . . . . . . . . . . 12
                      
                            
   
                
         |
| 84 | 83 | expl 648 |
. . . . . . . . . . 11
                     
                            
   
                
          |
| 85 | 84 | com24 95 |
. . . . . . . . . 10
                                        
                
                
       |
| 86 | 85 | rexlimiv 3027 |
. . . . . . . . 9
        
   
        
   
                
                
                    |
| 87 | 27, 28, 86 | syl2im 40 |
. . . . . . . 8
    
    
                
                
                    |
| 88 | 87 | imp 445 |
. . . . . . 7
    
            
   
                                 
        |
| 89 | 88 | com12 32 |
. . . . . 6
                
                 
   
                
        |
| 90 | 21, 26, 89 | syl2anc 693 |
. . . . 5
                       
                 
                
     |
| 91 | | mulsrpr 9897 |
. . . . . . 7
                       
       ![] ]](rbrack.gif)  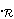       ![] ]](rbrack.gif)   
        
                
    ![] ]](rbrack.gif)   |
| 92 | 91 | breq2d 4665 |
. . . . . 6
                       
          ![] ]](rbrack.gif)  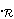       ![] ]](rbrack.gif)   
             
                  ![] ]](rbrack.gif)    |
| 93 | | gt0srpr 9899 |
. . . . . 6
                          
       ![] ]](rbrack.gif)                       
       |
| 94 | 92, 93 | syl6bb 276 |
. . . . 5
                       
          ![] ]](rbrack.gif)  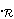       ![] ]](rbrack.gif)   
   
                
        |
| 95 | 90, 94 | sylibrd 249 |
. . . 4
                       
                    ![] ]](rbrack.gif)  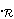       ![] ]](rbrack.gif)     |
| 96 | 20, 95 | syl5bi 232 |
. . 3
                       
          ![] ]](rbrack.gif)    
      ![] ]](rbrack.gif)     
       ![] ]](rbrack.gif)  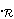       ![] ]](rbrack.gif)     |
| 97 | 7, 12, 17, 96 | 2ecoptocl 7838 |
. 2
     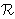   
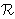                  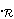     |
| 98 | 6, 97 | mpcom 38 |
1
    
           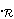    |