Theorem pclfinclN 35236

Description: The projective subspace closure of a finite set of atoms is a closed subspace. Compare the (non-closed) subspace version pclfinN 35186 and also pclcmpatN 35187. (Contributed by NM, 13-Sep-2013.) (New usage is discouraged.)

Hypotheses

Ref	Expression
pclfincl.a	|- A = ( Atoms ` K )
pclfincl.c	|- U = ( PCl ` K )
pclfincl.s	|- S = ( PSubCl ` K )

Assertion

Ref	Expression
pclfinclN	|- ( ( K e. HL /\ X C_ A /\ X e. Fin ) -> ( U ` X ) e. S )

Proof of Theorem pclfinclN

Dummy variables q p w x y z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		sseq1 3626	. . . . . 6 |- ( x = (/) -> ( x C_ A <-> (/) C_ A ) )
2	1	anbi2d 740	. . . . 5 |- ( x = (/) -> ( ( K e. HL /\ x C_ A ) <-> ( K e. HL /\ (/) C_ A ) ) )
3		fveq2 6191	. . . . . 6 |- ( x = (/) -> ( U ` x ) = ( U ` (/) ) )
4	3	eleq1d 2686	. . . . 5 |- ( x = (/) -> ( ( U ` x ) e. S <-> ( U ` (/) ) e. S ) )
5	2, 4	imbi12d 334	. . . 4 |- ( x = (/) -> ( ( ( K e. HL /\ x C_ A ) -> ( U ` x ) e. S ) <-> ( ( K e. HL /\ (/) C_ A ) -> ( U ` (/) ) e. S ) ) )
6		sseq1 3626	. . . . . 6 |- ( x = y -> ( x C_ A <-> y C_ A ) )
7	6	anbi2d 740	. . . . 5 |- ( x = y -> ( ( K e. HL /\ x C_ A ) <-> ( K e. HL /\ y C_ A ) ) )
8		fveq2 6191	. . . . . 6 |- ( x = y -> ( U ` x ) = ( U ` y ) )
9	8	eleq1d 2686	. . . . 5 |- ( x = y -> ( ( U ` x ) e. S <-> ( U ` y ) e. S ) )
10	7, 9	imbi12d 334	. . . 4 |- ( x = y -> ( ( ( K e. HL /\ x C_ A ) -> ( U ` x ) e. S ) <-> ( ( K e. HL /\ y C_ A ) -> ( U ` y ) e. S ) ) )
11		sseq1 3626	. . . . . 6 |- ( x = ( y u. { z } ) -> ( x C_ A <-> ( y u. { z } ) C_ A ) )
12	11	anbi2d 740	. . . . 5 |- ( x = ( y u. { z } ) -> ( ( K e. HL /\ x C_ A ) <-> ( K e. HL /\ ( y u. { z } ) C_ A ) ) )
13		fveq2 6191	. . . . . 6 |- ( x = ( y u. { z } ) -> ( U ` x ) = ( U ` ( y u. { z } ) ) )
14	13	eleq1d 2686	. . . . 5 |- ( x = ( y u. { z } ) -> ( ( U ` x ) e. S <-> ( U ` ( y u. { z } ) ) e. S ) )
15	12, 14	imbi12d 334	. . . 4 |- ( x = ( y u. { z } ) -> ( ( ( K e. HL /\ x C_ A ) -> ( U ` x ) e. S ) <-> ( ( K e. HL /\ ( y u. { z } ) C_ A ) -> ( U ` ( y u. { z } ) ) e. S ) ) )
16		sseq1 3626	. . . . . 6 |- ( x = X -> ( x C_ A <-> X C_ A ) )
17	16	anbi2d 740	. . . . 5 |- ( x = X -> ( ( K e. HL /\ x C_ A ) <-> ( K e. HL /\ X C_ A ) ) )
18		fveq2 6191	. . . . . 6 |- ( x = X -> ( U ` x ) = ( U ` X ) )
19	18	eleq1d 2686	. . . . 5 |- ( x = X -> ( ( U ` x ) e. S <-> ( U ` X ) e. S ) )
20	17, 19	imbi12d 334	. . . 4 |- ( x = X -> ( ( ( K e. HL /\ x C_ A ) -> ( U ` x ) e. S ) <-> ( ( K e. HL /\ X C_ A ) -> ( U ` X ) e. S ) ) )
21		pclfincl.c	. . . . . . 7 |- U = ( PCl ` K )
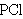22	21	pcl0N 35208	. . . . . 6 |- ( K e. HL -> ( U ` (/) ) = (/) )
23		pclfincl.s	. . . . . . 7 |- S = ( PSubCl ` K )
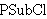24	23	0psubclN 35229	. . . . . 6 |- ( K e. HL -> (/) e. S )
25	22, 24	eqeltrd 2701	. . . . 5 |- ( K e. HL -> ( U ` (/) ) e. S )
26	25	adantr 481	. . . 4 |- ( ( K e. HL /\ (/) C_ A ) -> ( U ` (/) ) e. S )
27		anass 681	. . . . . . 7 |- ( ( ( K e. HL /\ y C_ A ) /\ z e. A ) <-> ( K e. HL /\ ( y C_ A /\ z e. A ) ) )
28		vex 3203	. . . . . . . . . . 11 |- z e. _V
29	28	snss 4316	. . . . . . . . . 10 |- ( z e. A <-> { z } C_ A )
30	29	anbi2i 730	. . . . . . . . 9 |- ( ( y C_ A /\ z e. A ) <-> ( y C_ A /\ { z } C_ A ) )
31		unss 3787	. . . . . . . . 9 |- ( ( y C_ A /\ { z } C_ A ) <-> ( y u. { z } ) C_ A )
32	30, 31	bitri 264	. . . . . . . 8 |- ( ( y C_ A /\ z e. A ) <-> ( y u. { z } ) C_ A )
33	32	anbi2i 730	. . . . . . 7 |- ( ( K e. HL /\ ( y C_ A /\ z e. A ) ) <-> ( K e. HL /\ ( y u. { z } ) C_ A ) )
34	27, 33	bitr2i 265	. . . . . 6 |- ( ( K e. HL /\ ( y u. { z } ) C_ A ) <-> ( ( K e. HL /\ y C_ A ) /\ z e. A ) )
35		simpllr 799	. . . . . . . . . . . . . . 15 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> y = (/) )
36	35	uneq1d 3766	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( y u. { z } ) = ( (/) u. { z } ) )
37		uncom 3757	. . . . . . . . . . . . . . 15 |- ( (/) u. { z } ) = ( { z } u. (/) )
38		un0 3967	. . . . . . . . . . . . . . 15 |- ( { z } u. (/) ) = { z }
39	37, 38	eqtri 2644	. . . . . . . . . . . . . 14 |- ( (/) u. { z } ) = { z }
40	36, 39	syl6eq 2672	. . . . . . . . . . . . 13 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( y u. { z } ) = { z } )
41	40	fveq2d 6195	. . . . . . . . . . . 12 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` ( y u. { z } ) ) = ( U ` { z } ) )
42		simplrl 800	. . . . . . . . . . . . 13 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> K e. HL )
43		hlatl 34647	. . . . . . . . . . . . . . 15 |- ( K e. HL -> K e. AtLat )
44	42, 43	syl 17	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> K e. AtLat )
45		simprr 796	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> z e. A )
46		pclfincl.a	. . . . . . . . . . . . . . 15 |- A = ( Atoms ` K )
47		eqid 2622	. . . . . . . . . . . . . . 15 |- ( PSubSp ` K ) = ( PSubSp ` K )
48	46, 47	snatpsubN 35036	. . . . . . . . . . . . . 14 |- ( ( K e. AtLat /\ z e. A ) -> { z } e. ( PSubSp ` K ) )
49	44, 45, 48	syl2anc 693	. . . . . . . . . . . . 13 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> { z } e. ( PSubSp ` K ) )
50	47, 21	pclidN 35182	. . . . . . . . . . . . 13 |- ( ( K e. HL /\ { z } e. ( PSubSp ` K ) ) -> ( U ` { z } ) = { z } )
51	42, 49, 50	syl2anc 693	. . . . . . . . . . . 12 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` { z } ) = { z } )
52	41, 51	eqtrd 2656	. . . . . . . . . . 11 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` ( y u. { z } ) ) = { z } )
53	46, 23	atpsubclN 35231	. . . . . . . . . . . 12 |- ( ( K e. HL /\ z e. A ) -> { z } e. S )
54	42, 45, 53	syl2anc 693	. . . . . . . . . . 11 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> { z } e. S )
55	52, 54	eqeltrd 2701	. . . . . . . . . 10 |- ( ( ( ( y e. Fin /\ y = (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` ( y u. { z } ) ) e. S )
56	55	exp43 640	. . . . . . . . 9 |- ( ( y e. Fin /\ y = (/) ) -> ( ( K e. HL /\ y C_ A ) -> ( ( U ` y ) e. S -> ( z e. A -> ( U ` ( y u. { z } ) ) e. S ) ) ) )
57		simplrl 800	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> K e. HL )
58	46, 21	pclssidN 35181	. . . . . . . . . . . . . . . . 17 |- ( ( K e. HL /\ y C_ A ) -> y C_ ( U ` y ) )
59	58	ad2antlr 763	. . . . . . . . . . . . . . . 16 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> y C_ ( U ` y ) )
60		unss1 3782	. . . . . . . . . . . . . . . 16 |- ( y C_ ( U ` y ) -> ( y u. { z } ) C_ ( ( U ` y ) u. { z } ) )
61	59, 60	syl 17	. . . . . . . . . . . . . . 15 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( y u. { z } ) C_ ( ( U ` y ) u. { z } ) )
62		simprl 794	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` y ) e. S )
63	46, 23	psubclssatN 35227	. . . . . . . . . . . . . . . . 17 |- ( ( K e. HL /\ ( U ` y ) e. S ) -> ( U ` y ) C_ A )
64	57, 62, 63	syl2anc 693	. . . . . . . . . . . . . . . 16 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` y ) C_ A )
65		snssi 4339	. . . . . . . . . . . . . . . . 17 |- ( z e. A -> { z } C_ A )
66	65	ad2antll 765	. . . . . . . . . . . . . . . 16 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> { z } C_ A )
67		eqid 2622	. . . . . . . . . . . . . . . . 17 |- ( +P ` K ) = ( +P ` K )
68	46, 67	paddunssN 35094	. . . . . . . . . . . . . . . 16 |- ( ( K e. HL /\ ( U ` y ) C_ A /\ { z } C_ A ) -> ( ( U ` y ) u. { z } ) C_ ( ( U ` y ) ( +P ` K ) { z } ) )
69	57, 64, 66, 68	syl3anc 1326	. . . . . . . . . . . . . . 15 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( ( U ` y ) u. { z } ) C_ ( ( U ` y ) ( +P ` K ) { z } ) )
70	61, 69	sstrd 3613	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( y u. { z } ) C_ ( ( U ` y ) ( +P ` K ) { z } ) )
71	46, 67	paddssat 35100	. . . . . . . . . . . . . . 15 |- ( ( K e. HL /\ ( U ` y ) C_ A /\ { z } C_ A ) -> ( ( U ` y ) ( +P ` K ) { z } ) C_ A )
72	57, 64, 66, 71	syl3anc 1326	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( ( U ` y ) ( +P ` K ) { z } ) C_ A )
73	46, 21	pclssN 35180	. . . . . . . . . . . . . 14 |- ( ( K e. HL /\ ( y u. { z } ) C_ ( ( U ` y ) ( +P ` K ) { z } ) /\ ( ( U ` y ) ( +P ` K ) { z } ) C_ A ) -> ( U ` ( y u. { z } ) ) C_ ( U ` ( ( U ` y ) ( +P ` K ) { z } ) ) )
74	57, 70, 72, 73	syl3anc 1326	. . . . . . . . . . . . 13 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` ( y u. { z } ) ) C_ ( U ` ( ( U ` y ) ( +P ` K ) { z } ) ) )
75		simprr 796	. . . . . . . . . . . . . . . 16 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> z e. A )
76	46, 67, 23	paddatclN 35235	. . . . . . . . . . . . . . . 16 |- ( ( K e. HL /\ ( U ` y ) e. S /\ z e. A ) -> ( ( U ` y ) ( +P ` K ) { z } ) e. S )
77	57, 62, 75, 76	syl3anc 1326	. . . . . . . . . . . . . . 15 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( ( U ` y ) ( +P ` K ) { z } ) e. S )
78	47, 23	psubclsubN 35226	. . . . . . . . . . . . . . 15 |- ( ( K e. HL /\ ( ( U ` y ) ( +P ` K ) { z } ) e. S ) -> ( ( U ` y ) ( +P ` K ) { z } ) e. ( PSubSp ` K ) )
79	57, 77, 78	syl2anc 693	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( ( U ` y ) ( +P ` K ) { z } ) e. ( PSubSp ` K ) )
80	47, 21	pclidN 35182	. . . . . . . . . . . . . 14 |- ( ( K e. HL /\ ( ( U ` y ) ( +P ` K ) { z } ) e. ( PSubSp ` K ) ) -> ( U ` ( ( U ` y ) ( +P ` K ) { z } ) ) = ( ( U ` y ) ( +P ` K ) { z } ) )
81	57, 79, 80	syl2anc 693	. . . . . . . . . . . . 13 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` ( ( U ` y ) ( +P ` K ) { z } ) ) = ( ( U ` y ) ( +P ` K ) { z } ) )
82	74, 81	sseqtrd 3641	. . . . . . . . . . . 12 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` ( y u. { z } ) ) C_ ( ( U ` y ) ( +P ` K ) { z } ) )
83		hllat 34650	. . . . . . . . . . . . . . . . . 18 |- ( K e. HL -> K e. Lat )
84	57, 83	syl 17	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> K e. Lat )
85		simpllr 799	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> y =/= (/) )
86	46, 21	pcl0bN 35209	. . . . . . . . . . . . . . . . . . . 20 |- ( ( K e. HL /\ y C_ A ) -> ( ( U ` y ) = (/) <-> y = (/) ) )
87	86	ad2antlr 763	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( ( U ` y ) = (/) <-> y = (/) ) )
88	87	necon3bid 2838	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( ( U ` y ) =/= (/) <-> y =/= (/) ) )
89	85, 88	mpbird 247	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` y ) =/= (/) )
90		eqid 2622	. . . . . . . . . . . . . . . . . 18 |- ( le ` K ) = ( le ` K )
91		eqid 2622	. . . . . . . . . . . . . . . . . 18 |- ( join ` K ) = ( join ` K )
92	90, 91, 46, 67	elpaddat 35090	. . . . . . . . . . . . . . . . 17 |- ( ( ( K e. Lat /\ ( U ` y ) C_ A /\ z e. A ) /\ ( U ` y ) =/= (/) ) -> ( q e. ( ( U ` y ) ( +P ` K ) { z } ) <-> ( q e. A /\ E. p e. ( U ` y ) q ( le ` K ) ( p ( join ` K ) z ) ) ) )
93	84, 64, 75, 89, 92	syl31anc 1329	. . . . . . . . . . . . . . . 16 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( q e. ( ( U ` y ) ( +P ` K ) { z } ) <-> ( q e. A /\ E. p e. ( U ` y ) q ( le ` K ) ( p ( join ` K ) z ) ) ) )
94		simp1rl 1126	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) -> K e. HL )
95	94	3ad2ant1 1082	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) -> K e. HL )
96	95	adantr 481	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> K e. HL )
97		simprl 794	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> w e. ( PSubSp ` K ) )
98		simpl13 1138	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> q e. A )
99		unss 3787	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( y C_ w /\ { z } C_ w ) <-> ( y u. { z } ) C_ w )
100		simpl 473	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( y C_ w /\ { z } C_ w ) -> y C_ w )
101	99, 100	sylbir 225	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( y u. { z } ) C_ w -> y C_ w )
102	101	ad2antll 765	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> y C_ w )
103		simpl2 1065	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> p e. ( U ` y ) )
104	47, 21	elpcliN 35179	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( ( K e. HL /\ y C_ w /\ w e. ( PSubSp ` K ) ) /\ p e. ( U ` y ) ) -> p e. w )
105	96, 102, 97, 103, 104	syl31anc 1329	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> p e. w )
106	28	snss 4316	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( z e. w <-> { z } C_ w )
107	106	biimpri 218	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( { z } C_ w -> z e. w )
108	107	adantl 482	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( y C_ w /\ { z } C_ w ) -> z e. w )
109	99, 108	sylbir 225	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( y u. { z } ) C_ w -> z e. w )
110	109	ad2antll 765	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> z e. w )
111		simpl3 1066	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> q ( le ` K ) ( p ( join ` K ) z ) )
112	90, 91, 46, 47	psubspi2N 35034	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( K e. HL /\ w e. ( PSubSp ` K ) /\ q e. A ) /\ ( p e. w /\ z e. w /\ q ( le ` K ) ( p ( join ` K ) z ) ) ) -> q e. w )
113	96, 97, 98, 105, 110, 111, 112	syl33anc 1341	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) /\ p e. ( U ` y ) /\ q ( le ` K ) ( p ( join ` K ) z ) ) /\ ( w e. ( PSubSp ` K ) /\ ( y u. { z } ) C_ w ) ) -> q e. w )
114	113	exp520 1288	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) -> ( p e. ( U ` y ) -> ( q ( le ` K ) ( p ( join ` K ) z ) -> ( w e. ( PSubSp ` K ) -> ( ( y u. { z } ) C_ w -> q e. w ) ) ) ) )
115	114	rexlimdv 3030	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) /\ q e. A ) -> ( E. p e. ( U ` y ) q ( le ` K ) ( p ( join ` K ) z ) -> ( w e. ( PSubSp ` K ) -> ( ( y u. { z } ) C_ w -> q e. w ) ) ) )
116	115	3expia 1267	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( q e. A -> ( E. p e. ( U ` y ) q ( le ` K ) ( p ( join ` K ) z ) -> ( w e. ( PSubSp ` K ) -> ( ( y u. { z } ) C_ w -> q e. w ) ) ) ) )
117	116	impd 447	. . . . . . . . . . . . . . . 16 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( ( q e. A /\ E. p e. ( U ` y ) q ( le ` K ) ( p ( join ` K ) z ) ) -> ( w e. ( PSubSp ` K ) -> ( ( y u. { z } ) C_ w -> q e. w ) ) ) )
118	93, 117	sylbid 230	. . . . . . . . . . . . . . 15 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( q e. ( ( U ` y ) ( +P ` K ) { z } ) -> ( w e. ( PSubSp ` K ) -> ( ( y u. { z } ) C_ w -> q e. w ) ) ) )
119	118	ralrimdv 2968	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( q e. ( ( U ` y ) ( +P ` K ) { z } ) -> A. w e. ( PSubSp ` K ) ( ( y u. { z } ) C_ w -> q e. w ) ) )
120		simplrr 801	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> y C_ A )
121	120, 75	jca 554	. . . . . . . . . . . . . . . 16 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( y C_ A /\ z e. A ) )
122	121, 32	sylib 208	. . . . . . . . . . . . . . 15 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( y u. { z } ) C_ A )
123		vex 3203	. . . . . . . . . . . . . . . 16 |- q e. _V
124	46, 47, 21, 123	elpclN 35178	. . . . . . . . . . . . . . 15 |- ( ( K e. HL /\ ( y u. { z } ) C_ A ) -> ( q e. ( U ` ( y u. { z } ) ) <-> A. w e. ( PSubSp ` K ) ( ( y u. { z } ) C_ w -> q e. w ) ) )
125	57, 122, 124	syl2anc 693	. . . . . . . . . . . . . 14 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( q e. ( U ` ( y u. { z } ) ) <-> A. w e. ( PSubSp ` K ) ( ( y u. { z } ) C_ w -> q e. w ) ) )
126	119, 125	sylibrd 249	. . . . . . . . . . . . 13 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( q e. ( ( U ` y ) ( +P ` K ) { z } ) -> q e. ( U ` ( y u. { z } ) ) ) )
127	126	ssrdv 3609	. . . . . . . . . . . 12 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( ( U ` y ) ( +P ` K ) { z } ) C_ ( U ` ( y u. { z } ) ) )
128	82, 127	eqssd 3620	. . . . . . . . . . 11 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` ( y u. { z } ) ) = ( ( U ` y ) ( +P ` K ) { z } ) )
129	128, 77	eqeltrd 2701	. . . . . . . . . 10 |- ( ( ( ( y e. Fin /\ y =/= (/) ) /\ ( K e. HL /\ y C_ A ) ) /\ ( ( U ` y ) e. S /\ z e. A ) ) -> ( U ` ( y u. { z } ) ) e. S )
130	129	exp43 640	. . . . . . . . 9 |- ( ( y e. Fin /\ y =/= (/) ) -> ( ( K e. HL /\ y C_ A ) -> ( ( U ` y ) e. S -> ( z e. A -> ( U ` ( y u. { z } ) ) e. S ) ) ) )
131	56, 130	pm2.61dane 2881	. . . . . . . 8 |- ( y e. Fin -> ( ( K e. HL /\ y C_ A ) -> ( ( U ` y ) e. S -> ( z e. A -> ( U ` ( y u. { z } ) ) e. S ) ) ) )
132	131	a2d 29	. . . . . . 7 |- ( y e. Fin -> ( ( ( K e. HL /\ y C_ A ) -> ( U ` y ) e. S ) -> ( ( K e. HL /\ y C_ A ) -> ( z e. A -> ( U ` ( y u. { z } ) ) e. S ) ) ) )
133	132	imp4b 613	. . . . . 6 |- ( ( y e. Fin /\ ( ( K e. HL /\ y C_ A ) -> ( U ` y ) e. S ) ) -> ( ( ( K e. HL /\ y C_ A ) /\ z e. A ) -> ( U ` ( y u. { z } ) ) e. S ) )
134	34, 133	syl5bi 232	. . . . 5 |- ( ( y e. Fin /\ ( ( K e. HL /\ y C_ A ) -> ( U ` y ) e. S ) ) -> ( ( K e. HL /\ ( y u. { z } ) C_ A ) -> ( U ` ( y u. { z } ) ) e. S ) )
135	134	ex 450	. . . 4 |- ( y e. Fin -> ( ( ( K e. HL /\ y C_ A ) -> ( U ` y ) e. S ) -> ( ( K e. HL /\ ( y u. { z } ) C_ A ) -> ( U ` ( y u. { z } ) ) e. S ) ) )
136	5, 10, 15, 20, 26, 135	findcard2 8200	. . 3 |- ( X e. Fin -> ( ( K e. HL /\ X C_ A ) -> ( U ` X ) e. S ) )
137	136	3impib 1262	. 2 |- ( ( X e. Fin /\ K e. HL /\ X C_ A ) -> ( U ` X ) e. S )
138	137	3coml 1272	1 |- ( ( K e. HL /\ X C_ A /\ X e. Fin ) -> ( U ` X ) e. S )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   A.wral 2912   E.wrex 2913   u. cun 3572   C_ wss 3574   (/)c0 3915   {csn 4177   class class class wbr 4653   ` cfv 5888  (class class class)co 6650   Fincfn 7955   lecple 15948   joincjn 16944   Latclat 17045   Atomscatm 34550   AtLatcal 34551   HLchlt 34637   PSubSpcpsubsp 34782   +Pcpadd 35081   PClcpclN 35173   PSubClcpscN 35220

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-riotaBAD 34239

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-undef 7399  df-1o 7560  df-er 7742  df-en 7956  df-fin 7959  df-preset 16928  df-poset 16946  df-plt 16958  df-lub 16974  df-glb 16975  df-join 16976  df-meet 16977  df-p0 17039  df-p1 17040  df-lat 17046  df-clat 17108  df-oposet 34463  df-ol 34465  df-oml 34466  df-covers 34553  df-ats 34554  df-atl 34585  df-cvlat 34609  df-hlat 34638  df-psubsp 34789  df-pmap 34790  df-padd 35082  df-pclN 35174  df-polarityN 35189  df-psubclN 35221

This theorem is referenced by: (None)