| Step | Hyp | Ref
| Expression |
|---|
| 1 | | dsmmlss.p |
. . 3
      s s  |
| 2 | | dsmmlss.h |
. . 3
        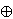 m m    |
| 3 | | dsmmlss.i |
. . 3
        |
| 4 | | dsmmlss.s |
. . 3
        |
| 5 | | dsmmlss.r |
. . . 4
          |
| 6 | | lmodgrp 18870 |
. . . . 5
    
     |
| 7 | 6 | ssriv 3607 |
. . . 4
    |
| 8 | | fss 6056 |
. . . 4
                    |
| 9 | 5, 7, 8 | sylancl 694 |
. . 3
          |
| 10 | 1, 2, 3, 4, 9 | dsmmsubg 20087 |
. 2
       SubGrp SubGrp    |
| 11 | | dsmmlss.k |
. . . . . . 7
    
      Scalar Scalar          |
| 12 | 1, 4, 3, 5, 11 | prdslmodd 18969 |
. . . . . 6
        |
| 13 | 12 | adantr 481 |
. . . . 5
    
       Scalar Scalar      
   
    |
| 14 | | simprl 794 |
. . . . 5
    
       Scalar Scalar      
   
      Scalar Scalar     |
| 15 | | simprr 796 |
. . . . . . 7
    
       Scalar Scalar      
   
    |
| 16 | | eqid 2622 |
. . . . . . . . 9
   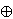 m m      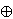 m m   |
| 17 | | eqid 2622 |
. . . . . . . . 9
            |
| 18 | | ffn 6045 |
. . . . . . . . . 10
            |
| 19 | 5, 18 | syl 17 |
. . . . . . . . 9
        |
| 20 | 1, 16, 17, 2, 3, 19 | dsmmelbas 20083 |
. . . . . . . 8
                                            |
| 21 | 20 | adantr 481 |
. . . . . . 7
    
       Scalar Scalar      
   
   
         
   
                      |
| 22 | 15, 21 | mpbid 222 |
. . . . . 6
    
       Scalar Scalar      
   
        
   
                     |
| 23 | 22 | simpld 475 |
. . . . 5
    
       Scalar Scalar      
   
        |
| 24 | | eqid 2622 |
. . . . . 6
  Scalar Scalar     Scalar Scalar   |
| 25 | | eqid 2622 |
. . . . . 6
            |
| 26 | | eqid 2622 |
. . . . . 6
     Scalar Scalar         Scalar Scalar    |
| 27 | 17, 24, 25, 26 | lmodvscl 18880 |
. . . . 5
             Scalar Scalar      
                       |
| 28 | 13, 14, 23, 27 | syl3anc 1326 |
. . . 4
    
       Scalar Scalar      
   
                |
| 29 | 22 | simprd 479 |
. . . . 5
    
       Scalar Scalar      
   
   
                    |
| 30 | | eqid 2622 |
. . . . . . . . . . 11
            |
| 31 | 4 | ad2antrr 762 |
. . . . . . . . . . 11
             Scalar Scalar    
       
       |
| 32 | 3 | ad2antrr 762 |
. . . . . . . . . . 11
             Scalar Scalar    
       
       |
| 33 | 19 | ad2antrr 762 |
. . . . . . . . . . 11
             Scalar Scalar    
       
       |
| 34 | | fex 6490 |
. . . . . . . . . . . . . . . . . 18
                  |
| 35 | 5, 3, 34 | syl2anc 693 |
. . . . . . . . . . . . . . . . 17
        |
| 36 | 1, 4, 35 | prdssca 16116 |
. . . . . . . . . . . . . . . 16
       Scalar Scalar    |
| 37 | 36 | fveq2d 6195 |
. . . . . . . . . . . . . . 15
              Scalar Scalar     |
| 38 | 37 | eleq2d 2687 |
. . . . . . . . . . . . . 14
                   Scalar Scalar      |
| 39 | 38 | biimpar 502 |
. . . . . . . . . . . . 13
    
      Scalar Scalar              |
| 40 | 39 | adantrr 753 |
. . . . . . . . . . . 12
    
       Scalar Scalar      
   
        |
| 41 | 40 | adantr 481 |
. . . . . . . . . . 11
             Scalar Scalar    
       
           |
| 42 | 23 | adantr 481 |
. . . . . . . . . . 11
             Scalar Scalar    
       
           |
| 43 | | simpr 477 |
. . . . . . . . . . 11
             Scalar Scalar    
       
       |
| 44 | 1, 17, 25, 30, 31, 32, 33, 41, 42, 43 | prdsvscafval 16140 |
. . . . . . . . . 10
             Scalar Scalar    
       
                                   |
| 45 | 44 | adantrr 753 |
. . . . . . . . 9
             Scalar Scalar    
       
                    
                                |
| 46 | 5 | ffvelrnda 6359 |
. . . . . . . . . . . . 13
    
             |
| 47 | 46 | adantlr 751 |
. . . . . . . . . . . 12
             Scalar Scalar    
       
           |
| 48 | | simplrl 800 |
. . . . . . . . . . . . 13
             Scalar Scalar    
       
         Scalar Scalar     |
| 49 | 36 | adantr 481 |
. . . . . . . . . . . . . . . 16
    
        Scalar Scalar    |
| 50 | 11, 49 | eqtrd 2656 |
. . . . . . . . . . . . . . 15
    
      Scalar Scalar         Scalar Scalar    |
| 51 | 50 | fveq2d 6195 |
. . . . . . . . . . . . . 14
    
         Scalar Scalar             Scalar Scalar     |
| 52 | 51 | adantlr 751 |
. . . . . . . . . . . . 13
             Scalar Scalar    
       
       Scalar Scalar             Scalar Scalar     |
| 53 | 48, 52 | eleqtrrd 2704 |
. . . . . . . . . . . 12
             Scalar Scalar    
       
         Scalar Scalar         |
| 54 | | eqid 2622 |
. . . . . . . . . . . . 13
  Scalar Scalar         Scalar Scalar       |
| 55 | | eqid 2622 |
. . . . . . . . . . . . 13
                    |
| 56 | | eqid 2622 |
. . . . . . . . . . . . 13
     Scalar Scalar             Scalar Scalar        |
| 57 | | eqid 2622 |
. . . . . . . . . . . . 13
                    |
| 58 | 54, 55, 56, 57 | lmodvs0 18897 |
. . . . . . . . . . . 12
                 Scalar Scalar                                          |
| 59 | 47, 53, 58 | syl2anc 693 |
. . . . . . . . . . 11
             Scalar Scalar    
       
                                   |
| 60 | | oveq2 6658 |
. . . . . . . . . . . 12
                 
                                        |
| 61 | 60 | eqeq1d 2624 |
. . . . . . . . . . 11
                 
                                                              |
| 62 | 59, 61 | syl5ibrcom 237 |
. . . . . . . . . 10
             Scalar Scalar    
       
                                                 |
| 63 | 62 | impr 649 |
. . . . . . . . 9
             Scalar Scalar    
       
                    
                            |
| 64 | 45, 63 | eqtrd 2656 |
. . . . . . . 8
             Scalar Scalar    
       
                    
                        |
| 65 | 64 | expr 643 |
. . . . . . 7
             Scalar Scalar    
       
                                             |
| 66 | 65 | necon3d 2815 |
. . . . . 6
             Scalar Scalar    
       
                                             |
| 67 | 66 | ss2rabdv 3683 |
. . . . 5
    
       Scalar Scalar      
   
   
                             
                  |
| 68 | | ssfi 8180 |
. . . . 5
                                                                                 
                              |
| 69 | 29, 67, 68 | syl2anc 693 |
. . . 4
    
       Scalar Scalar      
   
   
                            |
| 70 | 1, 16, 17, 2, 3, 19 | dsmmelbas 20083 |
. . . . 5
                                                                    |
| 71 | 70 | adantr 481 |
. . . 4
    
       Scalar Scalar      
   
            
                
   
                              |
| 72 | 28, 69, 71 | mpbir2and 957 |
. . 3
    
       Scalar Scalar      
   
            |
| 73 | 72 | ralrimivva 2971 |
. 2
           Scalar Scalar       
            |
| 74 | | dsmmlss.u |
. . . 4
        |
| 75 | 24, 26, 17, 25, 74 | islss4 18962 |
. . 3
    
     
    SubGrp SubGrp           Scalar Scalar       
              |
| 76 | 12, 75 | syl 17 |
. 2
             SubGrp SubGrp      
    Scalar Scalar                      |
| 77 | 10, 73, 76 | mpbir2and 957 |
1
        |