| Step | Hyp | Ref
| Expression |
|---|
| 1 | | opex 4932 |
. . 3
        |
| 2 | | opex 4932 |
. . 3
        |
| 3 | | eqeq1 2626 |
. . . . . . . 8
                     
          |
| 4 | | eqcom 2629 |
. . . . . . . 8
    
                     |
| 5 | 3, 4 | syl6bb 276 |
. . . . . . 7
                                |
| 6 | 5 | 3anbi1d 1403 |
. . . . . 6
                              
                   Cgr Cgr       
                                           Cgr Cgr         |
| 7 | 6 | rexbidv 3052 |
. . . . 5
                            
         
                   Cgr Cgr       
                                                   Cgr Cgr         |
| 8 | 7 | 2rexbidv 3057 |
. . . 4
                                            
         
                   Cgr Cgr       
                                                                   Cgr Cgr         |
| 9 | 8 | 2rexbidv 3057 |
. . 3
                                                        
         
                   Cgr Cgr       
                                                                               Cgr Cgr         |
| 10 | | eqeq1 2626 |
. . . . . . . 8
                     
          |
| 11 | | eqcom 2629 |
. . . . . . . 8
    
                     |
| 12 | 10, 11 | syl6bb 276 |
. . . . . . 7
                                |
| 13 | 12 | 3anbi2d 1404 |
. . . . . 6
                                  
                   Cgr Cgr       
                           
                   Cgr Cgr         |
| 14 | 13 | rexbidv 3052 |
. . . . 5
                                                              Cgr Cgr       
                                   
                   Cgr Cgr         |
| 15 | 14 | 2rexbidv 3057 |
. . . 4
                                                                              Cgr Cgr       
                                                   
                   Cgr Cgr         |
| 16 | 15 | 2rexbidv 3057 |
. . 3
                                                                                          Cgr Cgr       
                                                               
                   Cgr Cgr         |
| 17 | | df-segle 32214 |
. . 3
 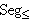                                                                                    Cgr Cgr        |
| 18 | 1, 2, 9, 16, 17 | brab 4998 |
. 2
    
  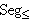   
     
                                                            
                   Cgr Cgr        |
| 19 | | vex 3203 |
. . . . . . . . 9
    |
| 20 | | vex 3203 |
. . . . . . . . 9
    |
| 21 | 19, 20 | opth 4945 |
. . . . . . . 8
                        |
| 22 | | vex 3203 |
. . . . . . . . 9
    |
| 23 | | vex 3203 |
. . . . . . . . 9
    |
| 24 | 22, 23 | opth 4945 |
. . . . . . . 8
                        |
| 25 | | biid 251 |
. . . . . . . 8
            
    
      Cgr Cgr                 
    
      Cgr Cgr       |
| 26 | 21, 24, 25 | 3anbi123i 1251 |
. . . . . . 7
                    
     
                      Cgr Cgr       
       
                                   Cgr Cgr        |
| 27 | 26 | 2rexbii 3042 |
. . . . . 6
                                    
     
                      Cgr Cgr       
                                 
                         Cgr Cgr        |
| 28 | 27 | 2rexbii 3042 |
. . . . 5
                                                    
     
                      Cgr Cgr       
                                                 
                         Cgr Cgr        |
| 29 | 28 | rexbii 3041 |
. . . 4
        
                                                        
                   Cgr Cgr       
                                                     
                         Cgr Cgr        |
| 30 | | simpl2l 1114 |
. . . . . . . . . . . . . . . . . . 19
                                              
           |
| 31 | 30 | ad2antrl 764 |
. . . . . . . . . . . . . . . . . 18
                                 
        
        
        
                                  
                 
        |
| 32 | | eleenn 25776 |
. . . . . . . . . . . . . . . . . 18
              |
| 33 | 31, 32 | syl 17 |
. . . . . . . . . . . . . . . . 17
                                 
        
        
        
                                  
                 
    |
| 34 | | simprlr 803 |
. . . . . . . . . . . . . . . . 17
                                 
        
        
        
                                  
                 
    |
| 35 | | simprll 802 |
. . . . . . . . . . . . . . . . . 18
                             
                 
            
                                     |
| 36 | 35 | adantl 482 |
. . . . . . . . . . . . . . . . 17
                                 
        
        
        
                                  
                 
        |
| 37 | | axdimuniq 25793 |
. . . . . . . . . . . . . . . . 17
                                 
  |
| 38 | 33, 31, 34, 36, 37 | syl22anc 1327 |
. . . . . . . . . . . . . . . 16
                                 
        
        
        
                                  
                 
    |
| 39 | 38 | fveq2d 6195 |
. . . . . . . . . . . . . . 15
                                 
        
        
        
                                  
                 
            |
| 40 | 39 | rexeqdv 3145 |
. . . . . . . . . . . . . 14
                                 
        
        
        
                                  
                 
   
                   Cgr Cgr                       
     Cgr Cgr        |
| 41 | 40 | exbiri 652 |
. . . . . . . . . . . . 13
                                                                      
            
                                           
        Cgr Cgr  
                    
     Cgr Cgr         |
| 42 | 41 | anassrs 680 |
. . . . . . . . . . . 12
                                 
        
        
        
                                  
                               
        Cgr Cgr  
                    
     Cgr Cgr         |
| 43 | | eleq1 2689 |
. . . . . . . . . . . . . . 15
              
         |
| 44 | | eleq1 2689 |
. . . . . . . . . . . . . . 15
              
         |
| 45 | 43, 44 | bi2anan9 917 |
. . . . . . . . . . . . . 14
        
            
                 
          |
| 46 | | eleq1 2689 |
. . . . . . . . . . . . . . 15
              
         |
| 47 | | eleq1 2689 |
. . . . . . . . . . . . . . 15
              
         |
| 48 | 46, 47 | bi2anan9 917 |
. . . . . . . . . . . . . 14
        
            
                 
          |
| 49 | 45, 48 | bi2anan9 917 |
. . . . . . . . . . . . 13
                                                      
                 
                             |
| 50 | 49 | anbi2d 740 |
. . . . . . . . . . . 12
                                 
        
        
        
                                          
                 
        
        
        
                                  
                  |
| 51 | | opeq12 4404 |
. . . . . . . . . . . . . . . . 17
        
               |
| 52 | 51 | breq1d 4663 |
. . . . . . . . . . . . . . . 16
        
         Cgr Cgr           Cgr Cgr       |
| 53 | 52 | anbi2d 740 |
. . . . . . . . . . . . . . 15
        
                  Cgr Cgr     
               Cgr Cgr        |
| 54 | | opeq12 4404 |
. . . . . . . . . . . . . . . . 17
        
               |
| 55 | 54 | breq2d 4665 |
. . . . . . . . . . . . . . . 16
        
           
    
    |
| 56 | | opeq1 4402 |
. . . . . . . . . . . . . . . . . 18
                  |
| 57 | 56 | breq2d 4665 |
. . . . . . . . . . . . . . . . 17
            Cgr Cgr        
  Cgr Cgr  
    |
| 58 | 57 | adantr 481 |
. . . . . . . . . . . . . . . 16
        
         Cgr Cgr        
  Cgr Cgr  
    |
| 59 | 55, 58 | anbi12d 747 |
. . . . . . . . . . . . . . 15
        
                  Cgr Cgr            
        Cgr Cgr  
     |
| 60 | 53, 59 | sylan9bb 736 |
. . . . . . . . . . . . . 14
                                       Cgr Cgr     
      
        Cgr Cgr  
     |
| 61 | 60 | rexbidv 3052 |
. . . . . . . . . . . . 13
                                               Cgr Cgr     
                 
     Cgr Cgr        |
| 62 | 61 | imbi1d 331 |
. . . . . . . . . . . 12
                                                Cgr Cgr     
              
        Cgr Cgr  
                   
        Cgr Cgr  
                    
     Cgr Cgr         |
| 63 | 42, 50, 62 | 3imtr4d 283 |
. . . . . . . . . . 11
                                 
        
        
        
                                          
        
   
                   Cgr Cgr     
              
        Cgr Cgr  
      |
| 64 | 63 | com12 32 |
. . . . . . . . . 10
                             
                 
            
                                     
                
        
    
      Cgr Cgr                       
     Cgr Cgr         |
| 65 | 64 | expd 452 |
. . . . . . . . 9
                             
                 
            
                                                  
   
                   Cgr Cgr     
              
        Cgr Cgr  
       |
| 66 | 65 | 3impd 1281 |
. . . . . . . 8
                             
                 
            
                                     
                                   Cgr Cgr                     
        Cgr Cgr  
     |
| 67 | 66 | expr 643 |
. . . . . . 7
                             
                 
                                        
                        
                   Cgr Cgr                     
        Cgr Cgr  
      |
| 68 | 67 | rexlimdvv 3037 |
. . . . . 6
                             
                 
                        
                                     
                   Cgr Cgr                     
        Cgr Cgr  
     |
| 69 | 68 | rexlimdvva 3038 |
. . . . 5
                                              
                                                     
                         Cgr Cgr       
             
        Cgr Cgr  
     |
| 70 | 69 | rexlimdva 3031 |
. . . 4
        
        
        
        
                                                              
                         Cgr Cgr       
             
        Cgr Cgr  
     |
| 71 | 29, 70 | syl5bi 232 |
. . 3
        
        
        
        
                                                                        
                   Cgr Cgr                     
        Cgr Cgr  
     |
| 72 | | simpl1 1064 |
. . . . 5
                                                       
     
     Cgr Cgr            |
| 73 | | simpl2l 1114 |
. . . . . 6
                                                       
     
     Cgr Cgr                |
| 74 | | simpl2r 1115 |
. . . . . 6
                                                       
     
     Cgr Cgr                |
| 75 | | simpl3l 1116 |
. . . . . . 7
                                                       
     
     Cgr Cgr                |
| 76 | | simpl3r 1117 |
. . . . . . 7
                                                       
     
     Cgr Cgr                |
| 77 | | eqidd 2623 |
. . . . . . 7
                                                       
     
     Cgr Cgr                    |
| 78 | | eqidd 2623 |
. . . . . . 7
                                                       
     
     Cgr Cgr                    |
| 79 | | simpr 477 |
. . . . . . 7
                                                       
     
     Cgr Cgr                     
        Cgr Cgr  
    |
| 80 | | opeq1 4402 |
. . . . . . . . . 10
                  |
| 81 | 80 | eqeq1d 2624 |
. . . . . . . . 9
                                |
| 82 | 80 | breq2d 4665 |
. . . . . . . . . . 11
        
    
          |
| 83 | 82, 57 | anbi12d 747 |
. . . . . . . . . 10
                     Cgr Cgr         
     
     Cgr Cgr        |
| 84 | 83 | rexbidv 3052 |
. . . . . . . . 9
        
        
    
      Cgr Cgr     
                 
     Cgr Cgr        |
| 85 | 81, 84 | 3anbi23d 1402 |
. . . . . . . 8
                         
     
                      Cgr Cgr       
                           
                   Cgr Cgr         |
| 86 | | opeq2 4403 |
. . . . . . . . . 10
                  |
| 87 | 86 | eqeq1d 2624 |
. . . . . . . . 9
                                |
| 88 | 86 | breq2d 4665 |
. . . . . . . . . . 11
        
       
       |
| 89 | 88 | anbi1d 741 |
. . . . . . . . . 10
               
     Cgr Cgr     
      
        Cgr Cgr  
     |
| 90 | 89 | rexbidv 3052 |
. . . . . . . . 9
        
        
     
     Cgr Cgr     
                 
     Cgr Cgr        |
| 91 | 87, 90 | 3anbi23d 1402 |
. . . . . . . 8
                         
     
             
        Cgr Cgr  
                 
           
             
        Cgr Cgr  
      |
| 92 | 85, 91 | rspc2ev 3324 |
. . . . . . 7
            
                                               
     Cgr Cgr          
                                                             Cgr Cgr        |
| 93 | 75, 76, 77, 78, 79, 92 | syl113anc 1338 |
. . . . . 6
                                                       
     
     Cgr Cgr                                    
    
         
                   Cgr Cgr        |
| 94 | | opeq1 4402 |
. . . . . . . . . 10
                  |
| 95 | 94 | eqeq1d 2624 |
. . . . . . . . 9
                                |
| 96 | 94 | breq1d 4663 |
. . . . . . . . . . 11
            Cgr Cgr        
  Cgr Cgr       |
| 97 | 96 | anbi2d 740 |
. . . . . . . . . 10
                     Cgr Cgr         
    
      Cgr Cgr        |
| 98 | 97 | rexbidv 3052 |
. . . . . . . . 9
        
        
    
      Cgr Cgr                 
    
      Cgr Cgr        |
| 99 | 95, 98 | 3anbi13d 1401 |
. . . . . . . 8
             
     
    
         
                   Cgr Cgr       
                           
                   Cgr Cgr         |
| 100 | 99 | 2rexbidv 3057 |
. . . . . . 7
        
                                
     
                      Cgr Cgr       
                            
    
         
                   Cgr Cgr         |
| 101 | | opeq2 4403 |
. . . . . . . . . 10
                  |
| 102 | 101 | eqeq1d 2624 |
. . . . . . . . 9
                                |
| 103 | 101 | breq1d 4663 |
. . . . . . . . . . 11
            Cgr Cgr        
  Cgr Cgr       |
| 104 | 103 | anbi2d 740 |
. . . . . . . . . 10
                     Cgr Cgr         
    
      Cgr Cgr        |
| 105 | 104 | rexbidv 3052 |
. . . . . . . . 9
        
        
    
      Cgr Cgr     
                       Cgr Cgr        |
| 106 | 102, 105 | 3anbi13d 1401 |
. . . . . . . 8
             
     
    
         
                   Cgr Cgr       
                           
                   Cgr Cgr         |
| 107 | 106 | 2rexbidv 3057 |
. . . . . . 7
        
                                
     
                      Cgr Cgr       
                            
    
         
                   Cgr Cgr         |
| 108 | 100, 107 | rspc2ev 3324 |
. . . . . 6
            
        
                         
    
         
                   Cgr Cgr          
                                                
     
                      Cgr Cgr        |
| 109 | 73, 74, 93, 108 | syl3anc 1326 |
. . . . 5
                                                       
     
     Cgr Cgr                                                                   
                   Cgr Cgr        |
| 110 | | fveq2 6191 |
. . . . . . 7
                  |
| 111 | 110 | rexeqdv 3145 |
. . . . . . . . . . 11
        
        
    
      Cgr Cgr                 
    
      Cgr Cgr        |
| 112 | 111 | 3anbi3d 1405 |
. . . . . . . . . 10
             
     
    
         
                   Cgr Cgr       
                           
                   Cgr Cgr         |
| 113 | 110, 112 | rexeqbidv 3153 |
. . . . . . . . 9
        
                        
     
                      Cgr Cgr       
                                   
                   Cgr Cgr         |
| 114 | 110, 113 | rexeqbidv 3153 |
. . . . . . . 8
        
                                
     
                      Cgr Cgr       
                                           
                   Cgr Cgr         |
| 115 | 110, 114 | rexeqbidv 3153 |
. . . . . . 7
        
                                        
     
                      Cgr Cgr       
                                                   
                   Cgr Cgr         |
| 116 | 110, 115 | rexeqbidv 3153 |
. . . . . 6
        
                                                
     
                      Cgr Cgr       
                                                           
                   Cgr Cgr         |
| 117 | 116 | rspcev 3309 |
. . . . 5
                                                         
     
                      Cgr Cgr          
                                                    
     
                      Cgr Cgr        |
| 118 | 72, 109, 117 | syl2anc 693 |
. . . 4
                                                       
     
     Cgr Cgr                                                                       
                   Cgr Cgr        |
| 119 | 118 | ex 450 |
. . 3
        
        
        
        
                      
        Cgr Cgr  
                                                          
     
                      Cgr Cgr         |
| 120 | 71, 119 | impbid 202 |
. 2
        
        
        
        
                                                                        
                   Cgr Cgr       
             
        Cgr Cgr  
     |
| 121 | 18, 120 | syl5bb 272 |
1
        
        
        
        
              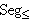        
        
     
     Cgr Cgr        |