Theorem lsat0cv 34320

Description: A subspace is an atom iff it covers the zero subspace. This could serve as an alternate definition of an atom. TODO: this is a quick-and-dirty proof that could probably be more efficient. (Contributed by NM, 14-Mar-2015.)

Hypotheses

Ref	Expression
lsat0cv.o	|- .0. = ( 0g ` W )
lsat0cv.s	|- S = ( LSubSp ` W )
lsat0cv.a	|- A = (LSAtoms ` W )
lsat0cv.c	|- C = ( <oLL ` W )
lsat0cv.w	|- ( ph -> W e. LVec )
lsat0cv.u	|- ( ph -> U e. S )

Assertion

Ref	Expression
lsat0cv	|- ( ph -> ( U e. A <-> { .0. } C U ) )

Proof of Theorem lsat0cv

Dummy variables x s are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		lsat0cv.o	. . 3 |- .0. = ( 0g ` W )
2		lsat0cv.a	. . 3 |- A = (LSAtoms ` W )
3		lsat0cv.c	. . 3 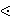|- C = ( <oLL ` W )
4		lsat0cv.w	. . . 4 |- ( ph -> W e. LVec )
5	4	adantr 481	. . 3 |- ( ( ph /\ U e. A ) -> W e. LVec )
6		simpr 477	. . 3 |- ( ( ph /\ U e. A ) -> U e. A )
7	1, 2, 3, 5, 6	lsatcv0 34318	. 2 |- ( ( ph /\ U e. A ) -> { .0. } C U )
8		lsat0cv.s	. . . . . . 7 |- S = ( LSubSp ` W )
9		lveclmod 19106	. . . . . . . . 9 |- ( W e. LVec -> W e. LMod )
10	4, 9	syl 17	. . . . . . . 8 |- ( ph -> W e. LMod )
11	10	adantr 481	. . . . . . 7 |- ( ( ph /\ { .0. } C U ) -> W e. LMod )
12	1, 8	lsssn0 18948	. . . . . . . . 9 |- ( W e. LMod -> { .0. } e. S )
13	10, 12	syl 17	. . . . . . . 8 |- ( ph -> { .0. } e. S )
14	13	adantr 481	. . . . . . 7 |- ( ( ph /\ { .0. } C U ) -> { .0. } e. S )
15		lsat0cv.u	. . . . . . . 8 |- ( ph -> U e. S )
16	15	adantr 481	. . . . . . 7 |- ( ( ph /\ { .0. } C U ) -> U e. S )
17		simpr 477	. . . . . . 7 |- ( ( ph /\ { .0. } C U ) -> { .0. } C U )
18	8, 3, 11, 14, 16, 17	lcvpss 34311	. . . . . 6 |- ( ( ph /\ { .0. } C U ) -> { .0. } C. U )
19		pssnel 4039	. . . . . 6 |- ( { .0. } C. U -> E. x ( x e. U /\ -. x e. { .0. } ) )
20	18, 19	syl 17	. . . . 5 |- ( ( ph /\ { .0. } C U ) -> E. x ( x e. U /\ -. x e. { .0. } ) )
21	15	ad2antrr 762	. . . . . . . . . . 11 |- ( ( ( ph /\ { .0. } C U ) /\ ( x e. U /\ -. x e. { .0. } ) ) -> U e. S )
22		simprl 794	. . . . . . . . . . 11 |- ( ( ( ph /\ { .0. } C U ) /\ ( x e. U /\ -. x e. { .0. } ) ) -> x e. U )
23		eqid 2622	. . . . . . . . . . . 12 |- ( Base ` W ) = ( Base ` W )
24	23, 8	lssel 18938	. . . . . . . . . . 11 |- ( ( U e. S /\ x e. U ) -> x e. ( Base ` W ) )
25	21, 22, 24	syl2anc 693	. . . . . . . . . 10 |- ( ( ( ph /\ { .0. } C U ) /\ ( x e. U /\ -. x e. { .0. } ) ) -> x e. ( Base ` W ) )
26		velsn 4193	. . . . . . . . . . . . . 14 |- ( x e. { .0. } <-> x = .0. )
27	26	biimpri 218	. . . . . . . . . . . . 13 |- ( x = .0. -> x e. { .0. } )
28	27	necon3bi 2820	. . . . . . . . . . . 12 |- ( -. x e. { .0. } -> x =/= .0. )
29	28	adantl 482	. . . . . . . . . . 11 |- ( ( x e. U /\ -. x e. { .0. } ) -> x =/= .0. )
30	29	adantl 482	. . . . . . . . . 10 |- ( ( ( ph /\ { .0. } C U ) /\ ( x e. U /\ -. x e. { .0. } ) ) -> x =/= .0. )
31		eldifsn 4317	. . . . . . . . . 10 |- ( x e. ( ( Base ` W ) \ { .0. } ) <-> ( x e. ( Base ` W ) /\ x =/= .0. ) )
32	25, 30, 31	sylanbrc 698	. . . . . . . . 9 |- ( ( ( ph /\ { .0. } C U ) /\ ( x e. U /\ -. x e. { .0. } ) ) -> x e. ( ( Base ` W ) \ { .0. } ) )
33	32, 22	jca 554	. . . . . . . 8 |- ( ( ( ph /\ { .0. } C U ) /\ ( x e. U /\ -. x e. { .0. } ) ) -> ( x e. ( ( Base ` W ) \ { .0. } ) /\ x e. U ) )
34	33	ex 450	. . . . . . 7 |- ( ( ph /\ { .0. } C U ) -> ( ( x e. U /\ -. x e. { .0. } ) -> ( x e. ( ( Base ` W ) \ { .0. } ) /\ x e. U ) ) )
35	34	eximdv 1846	. . . . . 6 |- ( ( ph /\ { .0. } C U ) -> ( E. x ( x e. U /\ -. x e. { .0. } ) -> E. x ( x e. ( ( Base ` W ) \ { .0. } ) /\ x e. U ) ) )
36		df-rex 2918	. . . . . 6 |- ( E. x e. ( ( Base ` W ) \ { .0. } ) x e. U <-> E. x ( x e. ( ( Base ` W ) \ { .0. } ) /\ x e. U ) )
37	35, 36	syl6ibr 242	. . . . 5 |- ( ( ph /\ { .0. } C U ) -> ( E. x ( x e. U /\ -. x e. { .0. } ) -> E. x e. ( ( Base ` W ) \ { .0. } ) x e. U ) )
38	20, 37	mpd 15	. . . 4 |- ( ( ph /\ { .0. } C U ) -> E. x e. ( ( Base ` W ) \ { .0. } ) x e. U )
39		simpllr 799	. . . . . . . 8 |- ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) -> { .0. } C U )
40	8, 3, 4, 13, 15	lcvbr2 34309	. . . . . . . . . . 11 |- ( ph -> ( { .0. } C U <-> ( { .0. } C. U /\ A. s e. S ( ( { .0. } C. s /\ s C_ U ) -> s = U ) ) ) )
41	40	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ { .0. } C U ) -> ( { .0. } C U <-> ( { .0. } C. U /\ A. s e. S ( ( { .0. } C. s /\ s C_ U ) -> s = U ) ) ) )
42	41	ad2antrr 762	. . . . . . . . 9 |- ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) -> ( { .0. } C U <-> ( { .0. } C. U /\ A. s e. S ( ( { .0. } C. s /\ s C_ U ) -> s = U ) ) ) )
43	10	ad2antrr 762	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) -> W e. LMod )
44	43	ad2antrr 762	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> W e. LMod )
45		eldifi 3732	. . . . . . . . . . . . . . . . 17 |- ( x e. ( ( Base ` W ) \ { .0. } ) -> x e. ( Base ` W ) )
46	45	adantl 482	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) -> x e. ( Base ` W ) )
47	46	ad2antrr 762	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> x e. ( Base ` W ) )
48		eqid 2622	. . . . . . . . . . . . . . . 16 |- ( LSpan ` W ) = ( LSpan ` W )
49	23, 8, 48	lspsncl 18977	. . . . . . . . . . . . . . 15 |- ( ( W e. LMod /\ x e. ( Base ` W ) ) -> ( ( LSpan ` W ) ` { x } ) e. S )
50	44, 47, 49	syl2anc 693	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> ( ( LSpan ` W ) ` { x } ) e. S )
51	1, 8	lss0ss 18949	. . . . . . . . . . . . . 14 |- ( ( W e. LMod /\ ( ( LSpan ` W ) ` { x } ) e. S ) -> { .0. } C_ ( ( LSpan ` W ) ` { x } ) )
52	44, 50, 51	syl2anc 693	. . . . . . . . . . . . 13 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> { .0. } C_ ( ( LSpan ` W ) ` { x } ) )
53		eldifsni 4320	. . . . . . . . . . . . . . . . 17 |- ( x e. ( ( Base ` W ) \ { .0. } ) -> x =/= .0. )
54	53	adantl 482	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) -> x =/= .0. )
55	54	ad2antrr 762	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> x =/= .0. )
56	23, 1, 48	lspsneq0 19012	. . . . . . . . . . . . . . . . 17 |- ( ( W e. LMod /\ x e. ( Base ` W ) ) -> ( ( ( LSpan ` W ) ` { x } ) = { .0. } <-> x = .0. ) )
57	44, 47, 56	syl2anc 693	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> ( ( ( LSpan ` W ) ` { x } ) = { .0. } <-> x = .0. ) )
58	57	necon3bid 2838	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> ( ( ( LSpan ` W ) ` { x } ) =/= { .0. } <-> x =/= .0. ) )
59	55, 58	mpbird 247	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> ( ( LSpan ` W ) ` { x } ) =/= { .0. } )
60	59	necomd 2849	. . . . . . . . . . . . 13 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> { .0. } =/= ( ( LSpan ` W ) ` { x } ) )
61		df-pss 3590	. . . . . . . . . . . . 13 |- ( { .0. } C. ( ( LSpan ` W ) ` { x } ) <-> ( { .0. } C_ ( ( LSpan ` W ) ` { x } ) /\ { .0. } =/= ( ( LSpan ` W ) ` { x } ) ) )
62	52, 60, 61	sylanbrc 698	. . . . . . . . . . . 12 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> { .0. } C. ( ( LSpan ` W ) ` { x } ) )
63	15	ad2antrr 762	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) -> U e. S )
64	63	ad2antrr 762	. . . . . . . . . . . . 13 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> U e. S )
65		simplr 792	. . . . . . . . . . . . 13 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> x e. U )
66	8, 48, 44, 64, 65	lspsnel5a 18996	. . . . . . . . . . . 12 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> ( ( LSpan ` W ) ` { x } ) C_ U )
67	62, 66	jca 554	. . . . . . . . . . 11 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> ( { .0. } C. ( ( LSpan ` W ) ` { x } ) /\ ( ( LSpan ` W ) ` { x } ) C_ U ) )
68		psseq2 3695	. . . . . . . . . . . . . . 15 |- ( s = ( ( LSpan ` W ) ` { x } ) -> ( { .0. } C. s <-> { .0. } C. ( ( LSpan ` W ) ` { x } ) ) )
69		sseq1 3626	. . . . . . . . . . . . . . 15 |- ( s = ( ( LSpan ` W ) ` { x } ) -> ( s C_ U <-> ( ( LSpan ` W ) ` { x } ) C_ U ) )
70	68, 69	anbi12d 747	. . . . . . . . . . . . . 14 |- ( s = ( ( LSpan ` W ) ` { x } ) -> ( ( { .0. } C. s /\ s C_ U ) <-> ( { .0. } C. ( ( LSpan ` W ) ` { x } ) /\ ( ( LSpan ` W ) ` { x } ) C_ U ) ) )
71		eqeq1 2626	. . . . . . . . . . . . . 14 |- ( s = ( ( LSpan ` W ) ` { x } ) -> ( s = U <-> ( ( LSpan ` W ) ` { x } ) = U ) )
72	70, 71	imbi12d 334	. . . . . . . . . . . . 13 |- ( s = ( ( LSpan ` W ) ` { x } ) -> ( ( ( { .0. } C. s /\ s C_ U ) -> s = U ) <-> ( ( { .0. } C. ( ( LSpan ` W ) ` { x } ) /\ ( ( LSpan ` W ) ` { x } ) C_ U ) -> ( ( LSpan ` W ) ` { x } ) = U ) ) )
73	72	rspcv 3305	. . . . . . . . . . . 12 |- ( ( ( LSpan ` W ) ` { x } ) e. S -> ( A. s e. S ( ( { .0. } C. s /\ s C_ U ) -> s = U ) -> ( ( { .0. } C. ( ( LSpan ` W ) ` { x } ) /\ ( ( LSpan ` W ) ` { x } ) C_ U ) -> ( ( LSpan ` W ) ` { x } ) = U ) ) )
74	50, 73	syl 17	. . . . . . . . . . 11 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> ( A. s e. S ( ( { .0. } C. s /\ s C_ U ) -> s = U ) -> ( ( { .0. } C. ( ( LSpan ` W ) ` { x } ) /\ ( ( LSpan ` W ) ` { x } ) C_ U ) -> ( ( LSpan ` W ) ` { x } ) = U ) ) )
75	67, 74	mpid 44	. . . . . . . . . 10 |- ( ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) /\ { .0. } C. U ) -> ( A. s e. S ( ( { .0. } C. s /\ s C_ U ) -> s = U ) -> ( ( LSpan ` W ) ` { x } ) = U ) )
76	75	expimpd 629	. . . . . . . . 9 |- ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) -> ( ( { .0. } C. U /\ A. s e. S ( ( { .0. } C. s /\ s C_ U ) -> s = U ) ) -> ( ( LSpan ` W ) ` { x } ) = U ) )
77	42, 76	sylbid 230	. . . . . . . 8 |- ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) -> ( { .0. } C U -> ( ( LSpan ` W ) ` { x } ) = U ) )
78	39, 77	mpd 15	. . . . . . 7 |- ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) -> ( ( LSpan ` W ) ` { x } ) = U )
79	78	eqcomd 2628	. . . . . 6 |- ( ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) /\ x e. U ) -> U = ( ( LSpan ` W ) ` { x } ) )
80	79	ex 450	. . . . 5 |- ( ( ( ph /\ { .0. } C U ) /\ x e. ( ( Base ` W ) \ { .0. } ) ) -> ( x e. U -> U = ( ( LSpan ` W ) ` { x } ) ) )
81	80	reximdva 3017	. . . 4 |- ( ( ph /\ { .0. } C U ) -> ( E. x e. ( ( Base ` W ) \ { .0. } ) x e. U -> E. x e. ( ( Base ` W ) \ { .0. } ) U = ( ( LSpan ` W ) ` { x } ) ) )
82	38, 81	mpd 15	. . 3 |- ( ( ph /\ { .0. } C U ) -> E. x e. ( ( Base ` W ) \ { .0. } ) U = ( ( LSpan ` W ) ` { x } ) )
83	4	adantr 481	. . . 4 |- ( ( ph /\ { .0. } C U ) -> W e. LVec )
84	23, 48, 1, 2	islsat 34278	. . . 4 |- ( W e. LVec -> ( U e. A <-> E. x e. ( ( Base ` W ) \ { .0. } ) U = ( ( LSpan ` W ) ` { x } ) ) )
85	83, 84	syl 17	. . 3 |- ( ( ph /\ { .0. } C U ) -> ( U e. A <-> E. x e. ( ( Base ` W ) \ { .0. } ) U = ( ( LSpan ` W ) ` { x } ) ) )
86	82, 85	mpbird 247	. 2 |- ( ( ph /\ { .0. } C U ) -> U e. A )
87	7, 86	impbida 877	1 |- ( ph -> ( U e. A <-> { .0. } C U ) )

Syntax hints:   -. wn 3   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   E.wex 1704   e. wcel 1990   =/= wne 2794   A.wral 2912   E.wrex 2913   \ cdif 3571   C_ wss 3574   C. wpss 3575   {csn 4177   class class class wbr 4653   ` cfv 5888   Basecbs 15857   0gc0g 16100   LModclmod 18863   LSubSpclss 18932   LSpanclspn 18971   LVecclvec 19102  LSAtomsclsa 34261   <oL_L clcv 34305

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-tpos 7352  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-er 7742  df-en 7956  df-dom 7957  df-sdom 7958  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-3 11080  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-plusg 15954  df-mulr 15955  df-0g 16102  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-grp 17425  df-minusg 17426  df-sbg 17427  df-cmn 18195  df-abl 18196  df-mgp 18490  df-ur 18502  df-ring 18549  df-oppr 18623  df-dvdsr 18641  df-unit 18642  df-invr 18672  df-drng 18749  df-lmod 18865  df-lss 18933  df-lsp 18972  df-lvec 19103  df-lsatoms 34263  df-lcv 34306

This theorem is referenced by:  mapdcnvatN  36955  mapdat  36956